Back to main menu
The delay of transmission
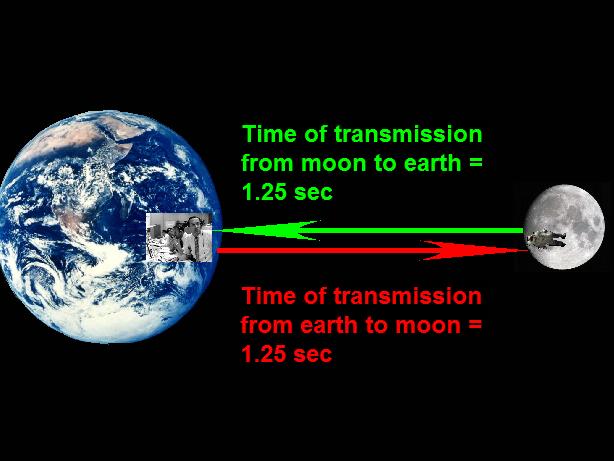
Given the distance of the moon to the earth (384000km) and the speed of the light (300000km/s), it takes 1.25 second for the light to go from the earth to the moon and vice versa (slightly more than 1.25 second, but I'll round it down to 1.25 second).
Thence the time of transmission of radio waves from the earth to the moon or from the moon to the earth cannot be less than 1.25 second (it is even slightly more, for the waves can be a little slowed down in earth's atmosphere, but we'll neglect it).
People use to think that it means that, in the discussion between the astronauts and Houston, there should be a delay of 1.25 second between each phrase of the dialog, that is as well between a question of an astronaut and the answer of the operator on earth as between a question of the operator and the answer of the astronaut.
But, it is wrong, for the answer of the astronaut is not recorded when it starts from the moon, but when it arrives on earth.
Therefore there is no delay in fact in the recording between a question of the astronaut and the reply of the operator in Houston.

On the other hand, between a question of the operator at Houston, and the answer of the astronaut, there must be the double of the time of transmission between the earth and the moon.
Indeed:
- It takes 1.25 second for the question of the operator to reach the astronaut
- The astronaut hears the question and answers to it.
- It then takes another 1.25 second for his answer to reach Houston where it is finally recorded.
So, between the recorded question of the operator and the recorded answer of the astronaut, there must be in fact 2*1.25=2.5 seconds, and not just 1.25 second.
This is an absolute minimum; this delay typically should even be over 3 seconds.
If you check the dialog between Houston (Parker) and the astronauts, you can effectively see that, when Parker talks, the astronauts generally reply no sooner than three seconds after Parker has finished talking.

This delay should always be observed, because, if it was not, it would mean that the astronauts are closer to Houston, and thence that the moon mission is not real.
I have stumbled on an interesting web page, made by someone who is not originally a moon hoaxer, a christian conservative who used to consider the moon hoaxers "kooks"; he used to find that their arguments were rather silly and certainly easy to debunk, and they were rather looking to him like anti-science people refusing a remarkable prowess.
But, what he saw about the delay of transmission left him dubitative, and led him to wonder if the moon-hoax people were really that pointless.

In a transmission of Apollo 11, Houston says to Collins, who has remained in the command module:
“I guess you’re about the only person around that doesn’t have TV coverage of the scene.”
And Collins replies:
“That’s alright, I don’t mind a bit.”
The problem is that, in the original live transmission (of which the sound graph is shown here), Collins makes his reply only 1.07 second after Houston has talked to him (meaning the time his reply is recorded is only separated by 1.07 second from the phrase of Houston).

But, in the new enhanced version of the NASA, this anomaly has been corrected, and NASA has added some filling so that the reply of Collins would now be separated from the phrase of Houston by a normal delay of transmission...
...But what's still more strange is that there is an echo before the reply of Collins which corresponds exactly to the delay of transmission, like it was a mark for placing the reply of Collins (or rather the actor who plays Collins).
So, now, those who listen to the latest version of this recording, and have not heard the original one, might think that there is no problem with the time of transmission on this discussion.

What else could we expect from the cheating NASA?

In fact, it is not necessary to search a long time to find other cases of wrong times of transmission.
You can find plenty of wrong times of transmission in Apollo 17 (I particularly like this mission, for it is the mission which is the richest in incoherences and surprises).
We can find a wrong time of transmission as soon as the beginning of Apollo 17 (at time 118:14:22).
In the transcript, there is the following dialog:
Parker: Hey, we have a picture, 17. We have a picture.
Cernan: You have? Ah, beautiful, babe. It's all yours. I hope it moves now.
Parker: It does.
Cernan: I hope it moves. You'll find out...

If we decompose it, we see the following phases:
1) Parker says: "Hey, we have a picture, 17. We have a picture."
2) Cernan replies: "You have?", but much too early, less than a half second after Parker has talked.
In fact he replies exactly like Parker was just next to him, in the same room.
3) After a little pause, Cernan goes on: "Ah, beautiful, babe. It's all yours. I hope it moves now."
4) Parker replies: "It does".
5) Cernan finally says: "I hope it moves. You'll find out", but again very shortly after Parker.
Now, you could say:
Parker repeats twice "We have a picture"; may be Cernan didn't wait for Parker to finish talking and replied to the first one.
But, even in that case, he is too early, for, between the end of the first "we have a picture" (green bar) and the beginning of the reply of Cernan (blue bar), there is only 1.8 seconds, so still less than the minimum delay of 2.5 seconds (even if he had replied to the first "we have a picture", he should have replied a second later).

There is another example of too fast reply of Schmitt at time 168:32:35.
Parker says:
"Okay, I copy. I understand"
And after a pause:
"But we'd like to get you going"
And, after a pause:
"In case you didn't get the clue."
And Schmitt immediately successively replies:
"I know"
Then:
"Look on".
Then:
"Okay"
This is the sound graph of the discussion; it is on a span of around 7.5 seconds.

If we decompose it, we see the following phases:
1) Parker says: "Okay, I copy. I understand." (I have colored it in dark blue)
2) Then Parker says: "But we'd like to get you going." (I have colored it in dark green)
3) And after a pause, Parker says: "In case you didn't get the clue." (I have colored it in red)
4) To the first part of Parker's phrase ("Okay, I copy. I understand"), Schmitt first replies "I know" (I have colored it in light blue); he replies 4.1 seconds after this part of phrase, which is a normal delay.
5) To the second part of Parker's phrase ("But we'd like to get you going"), Schmitt replies "Look on" (I have colored it in light green); he replies 3 seconds after this part of phrase, which is still a normal delay.
6) To the third part of parker's phrase ("In case you didn't get the clue"), Schmitt replies "Okay" (I have colored it in pink); this time, he only replies 1.4 second after this last part of phrase, which is a too short abnormal delay.

Besides the cases of astronauts simply replying too early, we also have some funnier cases of astronauts starting to reply too early, and repeating their reply at the correct time.
The first case I found is at time 142:49:05 in Apollo 17.
In the transcript, we find the following dialog:
Parker says:
"Okay. And John (Young) suggests that we might just check it momentarily while you're here to make sure it's still holding on good and tight. Both the clamps and the tape."
Cernan replies:
"Yeah, that's on my list"
It makes no doubt that Cernan answers to the last part of Parker's phrase, because he had to know what items parker was talking about (The clamps and the tape) before saying it was on his list.
This is the discussion between Houston and the astronaut, with the synchronized sound graph; it is on a span of around 12 seconds (11.5 seconds exactly).
(Click the start button to play it).

If we decompose it, we see the following phases:
1) Parker talks and says something to Cernan.
2) Cernan starts replying, but he replies less than one second after Parker has finished talking, and does not quite finish his phrase, visibly embarrassed.
3) Then we hear the end of the echo of Parker's voice.
4) Cernan makes his reply again, this time with the correct delay.

This is funnier that the astronaut just replying too early, because it puts into relief that the astronauts had to think about respecting the delay of transmission before replying, which is not so obvious in the heat of a discussion.

I have found another example of an astronaut replying too early and corrected by Houston, still funnier than the previous one.
This example is at time 169.28.09 in Apollo 17.
In the transcript, Parker talks to Schmitt and says:
"Copy that. We've also got SCB-3 with the Rover samples in it on the Rover, if you have any...yeah, you have some of those today."
And Schmitt replies:
"No, we emptied those into 5."
It makes no doubt that Schmitt answers to the last part of Parker's phrase, for he had to know what "those" Parker was talking about before saying what he had made of them.
This is the discussion between Houston and the astronaut, with the synchronized sound graph; it is on a span of around 11 seconds (10.5 seconds exactly).
(Click the start button to play it).

If we decompose it, we see the following phases:
1) Parker talks to Schmitt.
2) Schmitt immediately starts replying, but he just says "we" and stalls.
3) We hear a part of the echo of Parker's voice.
4) Schmitt starts replying again, but he is still too early and stops again after having said "we".
5) We hear the end of the echo of Parker's voice.
6) Finally Schmitt says his full reply with the good delay of transmission.
I have grayed the two times that Schmitt replies early on the sound graph.

So, this example is still funnier than with the example with Cernan, for Schmitt is not just early once on the delay of transmission, but even twice.
(Is there an example with an astronaut being early three times in a row? I don't think so, twice is already an exploit, LOL!).

Sometimes we hear the echo of Parker's voice, but not always.
Why so?
Because, when we hear the echo of Parker's voice, it is because it comes back through the microphone of the astronaut.
But, it can only come back if the microphone is activated; and, in order to activate the microphone, the astronaut had a switch which was allowing him to activate or disactivate the microphone (which was controlled by a "VOX control").
But, when the astronaut activates the vox control, we hear an activation click; conversely, when the astronaut disactivates the vox control, we hear a disactivation click; it looks like the sound we hear when someone gives the control back to his interlocutor in a CB, a little crack.
This visual and sound demo illustrates what happens; on it, we first hear the noise of silence because the sound control is current cut off, then an activation click, then the echo of Parker's voice, then a disactivation click, then the noise of silence again because the sound control is cut off again.
My example is perfectly realistic, for I have made it with parts I have picked from a video of Apollo 17.
(Click the start button to play it).
So, if, before the astronaut talks, we hear the echo of Parker's voice unfinished (i.e. if we go back 2.55 seconds after the end of the echo, we still find Parker talking), and that, between the premature end of the echo and the moment that the astronaut talks, we don't find two clicks (a disactivation click followed with an activation click), then it is clearly abnormal.
The echo seems to always be correctly delayed in the videos, but it is obvious that they were using an artificial way to generate it.

The first example of abnormal echo is at time 118.14.40 in Apollo 17.
In the script, Parker says:
"Okay, could we have a EMU check on you fellows when convenient?"
And Cernan replies:
" Okay. Commander is 3.8 plus. I must be 80 percent and no flags and no tones."
This is the discussion between Houston and the astronaut, with the synchronized sound graph; it is on a span of around 8.5 seconds.
(Click the start button to play it).

If we decompose it, we see the following phases:
1) Parker talks
2) We hear a beep
3) We hear an activation click of the microphone (I have colored it in yellow).
4) We hear the echo of the end of Parker's phrase, but not entirely.
The part I have colored in light green corresponds with the part I have colored in dark green in Parker's phrase.
The part I have colored in pink corresponds with the part I have colored in red in Parker's phrase, but it is mute, it is not the echo of the part colored in red, whereas it should normally be.
5) We finally hear the Cernan's answer.
It makes no doubt that we should have heard the complete echo of the end of parker's phrase, for, after the activation of the microphone (colored in yellow), the microphone is not disactivated before Cernan starts talking, otherwise we would hear a disactivation click and an activation click and see them on the sound graph, and we don't!
So the fact that the part I have colored in pink does not reproduce the echo of the part colored in red in Parker's phrase is clearly abnormal.
on this visual and sound example, I repeat 5 times the activation click we hear in the excerpt I have shown.
You can clearly hear that it looks like a switch click and not human voice.
(Click the start button to play it).

The second example of abnormal echo is at time 169.23.11 in Apollo 17.
In the script, Parker says:
"There's probably not very many convenient places to put it. That sounds like a good idea to me."
This is the discussion between Houston and the astronaut, with the synchronized sound graph; it is on a span of around 4.5 seconds.
(Click the start button to play it).

If we decompose it, we see the following phases:
1) Parker talks
2) We hear a beep
3) We hear Cernan say "Very Well", which means that the microphone is currently activated; we don't see an activation click between the beep and the moment Cernan starts talking, but it may have been activated in the same time as the beep, or while parker was talking.
4) We hear the echo of the end of Parker's phrase (I have colored it in light green, and I have colored the end of Parker's phrase, it is the echo of, in dark green); it is normal, since the microphone is still activated, but, there are two things which are less normal:
a) Cernan has answered before the end of the echo of Parker's phrase (may be he didn't wait for Parker to finish his phrase).
b) Between the beep and the moment Parker talked (part colored in pink), the microphone was activated, and this part corresponds to the echo of a part of Parker's phrase (that I have colored in red); so we should have heard the echo of this part, and we don't, it is mute.
Of course, you could say that the fact that there are missing parts on the echo could be explained by problems of transmissions, but it is really strange that these problems of transmission would repetitively happen on the echo of Parker's voice and never on the voices of the astronauts!

But the most original example of abnormal missing part of echo I have found is at time 169:22:00 in Apollo 17.
In the transcript Parker says to Cernan:
"I see where you've got a feedwater tone coming up pretty soon, Gene."
And Cernan replies:
" Bob, I already got it and I'm in Auto. Just about 30 seconds ago."
This is the discussion between Houston and the astronaut, with the synchronized sound graph; it is on a span of around 9 seconds (A little less).
(Click the start button to play it).

If we decompose it, we see the following phases:
1) Parker talks to Cernan
2) There is a beep
3) We then hear the echo of Parker's voice.
4) Then Cernan replies, with a normal delay (or almost).
5) Finally we hear a double beep
The blue bar indicates the end of Parker's voice, and the green bar the end of the echo of Parker's voice.
Between the two there should be the delay of transmission to and back from the moon, so no less than 2.5 seconds (typically 2.6 seconds).
But, if we measure on the sound graph, we find only 2 seconds (somewhere between 2 and 2.1 seconds), definitively less than the normal delay; I have indicated with a red bar where the end of the echo of parker's voice (the green bar) should have been.
In fact, it is not because the echo of parker's voice is incorrectly delayed, but because the end of parker's voice is missing on the echo; there is around a half second missing on the echo; it is abnormal, for the microphone has not been disactivated; we don't hear a disactivation click and an activation click before Cernan replies, and besides Cernan replies very shortly after the end of the echo.
If the end of Parker's voice is missing on the echo and the microphone was activated, that means that Cernan could not hear the end of parker's phrase; yet, this end was containing Cernan's first name (Gene).
So, Cernan could not know that Parker was speaking to him; he could eventually have guessed, if Parker had given him a clue, but Parker talks to him about a feedwater tone soon coming, ignoring that it has already come 30 seconds ago for Cernan; so Cernan might have thought that Parker was talking to Schmitt rather than to him unless he had heard that Parker was specifically talking to him, which he didn't.
There is clearly a contradiction here!

I have found another original case of strange echo.
It is at time 119.14.17 in Apollo 17.
In the transcript, Parker says:
"Roger. Understand you also have the heat flow connector connected by now?"
And Schmitt replies:
"Yes sir".
This is the discussion between Houston and the astronaut, with the synchronized sound graph; it is on a span of around 6 seconds.
(Click the start button to play it).

If we analyze this sound graph, we can see that the echo is complete and correctly delayed.
So what's the problem with it?
The problem is that the echo (colored in pink) is as loud as Parker's voice (colored in red), of which it obviously seems to be a replication on the sound graph; it even seems to be a little louder than Schmitt's voice (colored in yellow).
Normally the echo is fainter than the voices of the operator and the astronauts; indeed it comes to the microphone from the earphones, and it so appears muffled relatively to the voice of the astronauts, since their mouth is closer to the microphone than their earphones.
If the echo of Parker's voice is as loud as his own voice, then we should hear a third echo, the echo of the echo; how comes we don't hear it?
And since the echo of Parker's voice is louder than in other occasions, that means that the astronaut would have put the earphones closer to the microphone (it can't be explained by the fact that he just increased the level of the microphone, otherwise the level of his voice would have been increased too; besides he only had a switch to activate or disactivate the microphone, but not to adjust its level).

But, if you, on earth, could remove your headphone from your ears and put it close to the microphone, so that the echo of someone talking to you would be louder (but you would create a hell of a larsen!), such was not the case for the astronauts who had no possibility of doing it, as they could not remove their suit...

...unless their suit was fake, and they could easily remove it on the fake moonset!













