I Apologize for the POP-UP Ads - But they keep my site free! Just minimize it!
(Don't close it, or a new one pops up every page you visit!)
you are this site's visitor number
Powered by counter.bloke.com


What is this  stuff, anyway?
stuff, anyway?

We use numerals (1,2,3,4,5 etc.) to represent numbers of things.
If we were to try to use the actual objects, it could be pretty hard to do.
For example: If I wanted to tell a friend how many cookies I made last night, I might have trouble showing her the actual cookies because I already ate so many, or, if we were talking about the huge numbers of people in New York City, we certainly couldn't get them all to stand still in one place. So you see, it's a lot easier to use numerals to represent numbers of things.
The numeral '1' represents one unit of something, like one small blue block.

A unit is one of whatever you are dealing with - if you have cookies to count, one cookie would be a unit.
If you are counting sacks full of oranges, one sack of oranges would be your unit.
In our counting system, we base everything on sets of ten, so we call it a
"Base 10 System"
!!When we write numerals, each position represents a unit or sets of 10 units, etc.
The position of the numeral shows us its place and its value, so we call that its "place value". !!
You start with just one

10 ones = one set of ten

10 sets of ten = one set of one hundred
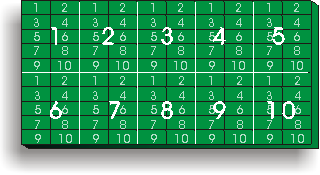
10 sets of one hundred = one set of one thousand
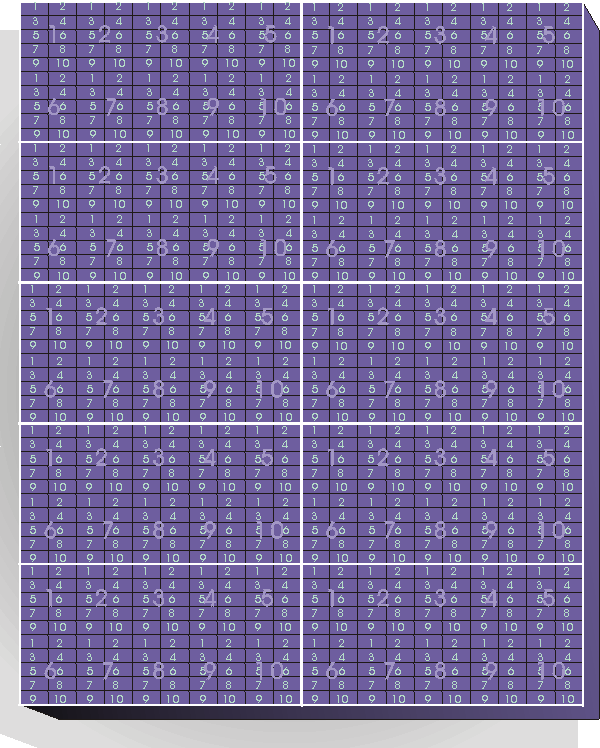
10 sets of one thousand = one set of ten thousand
(alright, you have to use your imagination now, the 10,000 blocks and larger are just too big to put on here!)
10 sets of ten thousand = one set of one hundred thousand
10 sets of one hundred thousand = one set of one million
10 sets of one million = one set of ten million
10 sets of ten million = one set of one hundred million
10 sets of one hundred million = one billion
and on and on..........yup, to infinity...it just goes on forever!
The cool thing about it is, that if you learn how to add, subtract, multiply and divide
with ones and tens, you can do any amount, because it all follows the same patterns!
Even with decimals!!
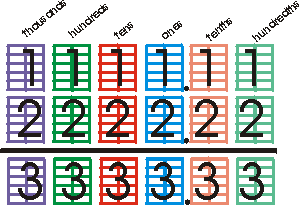
1 one-hundredth + 2 one-hundredths = 3 one-hundredths
1 one + 2 ones = 3 ones
1 set of ten thousand + 2 sets of ten thousand = 3 sets of ten thousand

* 10 units of any set = 1 unit in the next larger set*

If your totals come up with 10 units of any set,
you have 1 unit in the next larger set.
!!No matter which side of the little period, or "decimal", you start on, the units go up in size as you move to the left, and they get smaller as you move to the right.
Starting at the decimal and moving to the left, we have ones, tens, hundreds, thousands, ten thousands, hundred thousands, millions, ten millions, hundred millions, billions, ten billions, hundred millions, trillions, (whew!... I'm getting tired here...) and the same thing works going to the right of the decimal, with tenths, hundredths, thousandths, ten thousandths, hundred thousandths, and I hope you don't actually have to got that far, but it just keeps going and going. The Energizer Bunny has nothing on numbers, let me tell you!
Did you notice that the places to the right side of the decimal all end in "th"s? That's because as you move to the right for each place, the unit is divided into ten smaller pieces each time - one (1 or 1.0) equals ten 'tenths', and one 'tenth' (1/10 or 0.1) equals ten 'hundredths''. One 'hundredth' (1/100 or 0.01) equals ten thounsandths', and one 'thousandth' (1/1000 or 0.001) equals ten 'ten thousandths'', and so on, ad infinitum. (that means it goes on to infinity, and that means you can never get to the end!! Some people have tried, but since you can never get to infinity, noone could live long enough to count that far - computers can't even do it!) !!


MILLIMETERS OR INCHES???
WHY DO SOME PEOPLE USE A RULER WITH INCHES
AND OTHERS USE RULERS WITH MILLIMETERS?
Good question! There is some controversy in the US over which system of measurement should be used; Our current system of English measurement, which uses a non-base 10 system for linear measurement (twelve inches =1 foot, 3 feet = 1 yard), a non-base 10 system for volume measurement (8 ounces = 1 cup, 4 cups = 1 quart), etc.; or the METRIC system, which is used in most of the world, and is a base 10 system. (10 millimeters = 1 centimeter, 10 centimeters = 1 decimeter, 10 decimeters =1 meter, and cubic centimeters for volume measurement and so on.) Even though we may be used to the English system, there is a lot to be said for being consistent, and for using a universally accepted system. It would make international commerce and communication less frustrating, and we would only have to deal with one system, instead of having to figure out how to convert whenever we change from measuring amounts to measuring distance, to measuring volume, and back and forth repeatedly. If we go ahead and adopt the world standard Metric system, some of us would have a bit of trouble adjusting at first, but in the long run, many people think we would all be better off. What do you think?
Do you know that there was an effort made to get this change implemented way back in the 1960s? People thought it would be too hard, and that we didn't need to match the rest of the world. Now, though, with the advent of the internet, and much more global interaction, it seems to make a lot of sense.
NOTE: This page and all graphics on it are
copyright ©1999 by Sarah A. McUmber-House, Sassafrass Grove Studio
all rights reserved.

Return to Sassafrass Grove Math Page
Return to Sassafrass Grove Main Page











