back to "Education" website

MATH 104 - Introduction to Statistics

WEEK 1 - Sept. 3

WEEK 1 - Sept. 4

WEEK 2 - Sept. 8

WEEK 2 - Sept. 10

WEEK 2 - Sept. 11

Summary: Today's class was a basic introduction to statistics.  We discussed what we has a class though of when we heard the word statistics and the prof. went over the different types of stats and methods of achieving stats that we would be learning throughout the course.

• What do you think of when you think of when you hear "statistics"?
  • Population.  Population of... British-Columbia = 4m, Canada = 31m, USA = 270m, World = 6m, Abbotsford = 120,000
  • Environment. examples... forestry (how many hectares), salmon (how many this season compared to the last), weather,   temperature, rainfall...
  • Traffic/Transportation. example... how many accidents happen per day
  • Business.  sale forecasting, stock market (example, it's up and down, you want to be able to forecast when it'll go back up, time series), consumer price index (CPI) inflation...
  • Jobs/Employment.  example... the unemployment/employment rate
  • Sports. example... an individual players stats, in football if you are the punter - how many yard average do you have, average hang time, average yards returned
  • Every area can have stats   
• Statistics is the science of gaining information from data.
• When we talk about stats we need data...  from the data, you need to gain information.  example: on average, how much is spend on textbooks per student?  <-- there are many different applications to get this data.

Stats in Practice

1. Data Analysis:  concerns, methods and ideas for organizing and describing the patterns of data using graphs, numerical summaries, etc.  We want to analyze this data by organizing the patters.  You can do this via graphs such as bar, pie, histograms, stemplots, etc.  You can also do this via numerical summary: come up with the mean (average), median (the middle number), standard deviation, etc.

For the last 10 years people are talking about statistical thinking.  You look at the big picture.  ¿What is stats all about?  <-- DATA.  You will be dealing with uncertainty, variation.  You need to deal with a lot of variation, example: weight of 1 student = 120, get another student to measure the weight, they will be a different number, there will be a different variation.  Dealing with different numbers... ¿How can we take this data and deal with it with all the uncertainty?  <-- variation.  Example:  driving to U.C.F.V. one day may take 15m30s, the next day it may take 16m50s, the third day it may rain and it will take even longer.  You want to find an average (mean) of how long it takes to drive. **you need to come up with the data and use it properly**

    2.    Data Production:  ¿How can you produce it?  Sampling and design of experiments are the main methods.  Sampling: ex. get peoples opinions (opinion polls) Example: 2010 bid, yes or no?  There is no control, you just get the data.  Example 2: Take Aspirin vs. a new drug.  You want to compare them, and when you give them to the patients, you have no control.  However you DO need to control who gets which drug to test because you don't know if the results are true if they are given to a certain majority.  If you give Aspirin to old people, mostly male, there may be a difference comparing it to the new drug you you may get it tested by young women.  This is why you need to do a random sampling to ensure that there is a vast difference in your sample and the two drugs get compared equally.

    3.    Statistical Indifference:  draws conclusions about the population from which a set of data is drawn.  It should be accomplished with a statement of reliability.  EX. 1:  Working class in BC (pop. approx. 3m)  p=proportion of people without jobs (true unemployment rate).  You need to get information from each and every unit - this is called a census (which is costly and time consuming).  In stats we think of shortcuts, so this is why we do sampling.  From the sample we take of the population of BC, we ask the question ¿do you work, yes or no?  Then we do the counting... lets say 16 people are unemployed out of the 200 people we sampled, so the sample proportion is 16/200 which = 8%.  But how can we make that a reliable statement?  Simple, we say that the 8% +/- (plus or minus) 2% meaning the true value is 6% - 10%

*end of day 1, back top of the page*

WEEK 1 - Sept. 4

Terms

1. Population: is a set of units or individuals.  example: people, objects, events, people in the working class, families in BC...

2. Variable of Interest: a characteristic of a population unit.  example: is the person employed or unemployed?  how much a family earns a year...

3. Sample: is a subset of the population units

Data

There are two types of variable data.

1. Categorical Variable: is one that can be classified into one or several categories.  example: eye color (blue, brown, hazel, green...)  Categorical variables are also known as qualitative variables.  A categorical variable can be displayed in either a bar graph or pie chart.

2. Quantitative Variable: takes numerical values only.  example: income, age...  A quantitative variable can be displayed through histograms.

Histograms

• If you are given 15 numbers (weight or 15 football players), 15 quantitative (numerical) observations: 210, 243, 227, 235, 274, 250, 242, 265, 245, 291, 243, 282, 276, 314, 245

• The above is an example of a histogram.  We need to know how the data points are distributed.  We need to define class intervals to that each observation can be classified into one and only one class interval.  MIN --> MAX = sample range (largest observation minus smallest observation)  example: 314 (largest) minus 210 (smallest) = 104 therefore interval is between 5-12.

• A relative frequency distribution table:

  Class Interval	Tally	Frequency	Relative Frequency
  200 - 220	I	1	1/15
  220 - 240	II	2	2/15
  240 - 260	VI	6	6/15
  260 - 280	III	3	3/15
  280 - 300	II	2	2/15
  300 - 320	I	1	1/15
  	Total=	15	1, 100%

• ¿If you pick a random football player, what are the chances they would weigh between 260-280lbs?  A = 20% 
• If an observation is drawn from the population P(260< x <280) is expected to be 3/15 = 20%
• An outlier is an extreme min or max compared to the other data
• The modal class is the class with the highest frequency  example: (240,260) mode = (240 + 260)/2, = 250

Chart Types

• View example of Frequency Chart  (this chart classified as a normal symmetric bell-shaped chart)
• A Relative Frequency Chart is basically the same as the frequency chart except that the values are in the fractional form
• A chart that is said to be skew to the right means that the tail of the chart points to the right
• A chart that is said to be skew to the left means that the tail of the chart points to the left

Stem plots

• (stem - and - leaf displays)
• Given a set of numerical data X₁, X₂... X_n, we split each number into two parts.  The stem consists of all the number except the final digit (this includes decimals too).  The leaf consists only of the final digit in the number.  Example: X₁ = 47 (4 is the stem, 7 is the leaf), in the case of a decimal, it would be as so: 14.7 (stem = 14, leaf = 7)
• When displaying the stem and leaf in a table format, any of the stems in the data that have the same first digits, their stems will be listed on the same line under the leaf category.  Example:  X₁ = 47, X₂ = 52, X₃ = 59

• When you make a table, such as the one above, you must also specify the values of the numbers.  By specifying the values one can tell whether there is a decimal involved or not (stem unit 10 x .1 =1)

*end of Sept. 4, return to top*

WEEK 2 - Sept. 8

This week's class was our Monday computer lab class.  In the computer lab we went over a brief overview of how to use Excel and Minitab.  Not many notes were taken for this class because most of the work is done on the computer.  Each program has a help section where you can go if you do not know how to do something or cannot remember how to do it.  Minitab is available at www.minitab.com for a free 30-day trial.  Sometimes if you move the date back on your computers calendar clock, you can keep an indefinite 30-day trial period ;)

*end of Sept. 8, back top of the page*

WEEK 2 - Sept. 10

Stem plots

1. The number of stems chosen should be between 5 and 12

2. You may need to do some rounding in order to achieve this.  example: 3.57 = 3.6, 4.12 = 4.1, 4.78 = 4.8  You want to round for simplicity because if you left those numbers as is, then you would have to put data entries from 3.5 all the way to 4.8 (3.6, 3.7, 3.8...) which takes a long time, that is why we round.  We may need to round (in Minitab it's called truncate) the date points so that the last digit is suitable for being a leaf.

3. Split Stems example:

Age 41, 44, 47, 49, 50, 55, 62, 66   <-- we can split these ages into early and later years (e.g.. early 40's, late 40's)

Numerical Descriptive Stats

1. You want to know the center
2. You need to know the variation of the spread of the data

• by measuring the center (mean, median), you need to locate the center of a data set.  The mean (x-bar) of a data set (X1, X2,...Xn) is the average value of the data set

These to the left are some math equations.  E equals the sum of many numbers.  Whenever you see a letter 'i' beside an E it represents the number that is shown next to the the X.  n represents the amount of data in the data set.  example: {4,5,6,8,7} <-- n would equal 5 because there are 5 numbers in that data set. **whenever you read "X-bar" in these notes, it means the symbol with the X and a bar overtop of it **

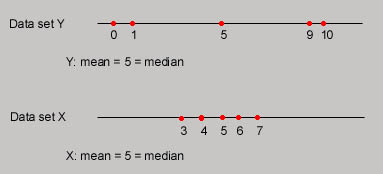
There are two kinds of means:

1. Population Mean (mu): this mean is usually an unknown quantity
2. Sample Mean (X-bar): this mean is a computable value that varies from sample to sample.  We use X-bar to estimate mu.  Given a sample in ascending order (smallest to largest), the same median (middle number) is defined by the middle number if n is odd.  If n is even, then to find the median, you take the average of the two middle numbers.  example: n = 9, (n+1)/2, (9+1)/2, 10/2, = 5  The answer 5 means it is the 5th number in the data set.  example 2: n = 8, n/2 (<-- gives us the first number), (n/2) + 1 (<-- gives us the second number) then you take the average of these two answers.

How a mean and median depict the form of a graph

• if the mean is > median, the data set (graph) is skewed to the right
• if the mean is < median, the data set (graph) is skewed to the left
• if the mean is = median, the data set (graph) is symmetrical (bell shaped)

A mode is a measurement that occurs most frequently in the data set.  Example: (quiz scores) 8,9,6,7,8,7,8 the mode = 8 (because it was the most common quiz score).  It is possible to have more than one mode.  If a curve is bell shaped/normal, then that means that the mean=median=mode (they are all equal)

Quartiles : comes from quarter, four equal parts (data sets with 4 equal parts)

• Q1: the midpoint of the observations on the left of the median
• Q3: the midpoint of the observations on the right of the median

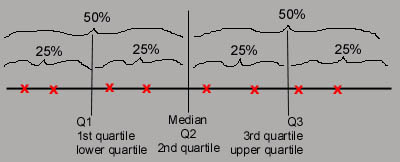
*end of Sept. 10, back top of the page*

WEEK 2 - Sept. 11

Equations for finding M, Q1 and Q3: they basically all share the same equation (n+1)/2.  Remember that the n in each of these equations represents the amount of data in each section.  So for M the n represents ALL the data in the data set.  for Q1 n represents the amount of data left of the median, and for Q3 n represents all the data right of the median.

Box Plots

• a box plot is a 5 number summary.  The first number is the MIN, then Q1, then the M, then Q3, and then the MAX
• the box represents the middle 50%
• the interquartile range (IQR) is the results of Q3 - Q1
• a horizontal line (known as whisker) is drawn from Q1 or Q3 up to the most extreme measurement insider the inner fence
• to determine the outlier, you just do 1.5 x IQR
• to VIEW an example of what box plot looks like, click on this link.  It also gives a histogram example

Interpretation 

1. The length of the box (IQR) can be used to compare the variability of 2 samples.  A more variable sample will have a bell-shaped curve, a less variable example will be skewed to either the left of right.
2. If one whisker is longer, then the distribution of the data is skewed in the direction of the longer whisker
3. Measurements that fall beyond the inner fences are considered outliers.  Outliers are extreme measurements that stand out from the rest of the sample.  

Three Reasons of having an Outlier

They may be... 

1. incorrectly measured, recorded, or entered into the computer
2. members of a different population than the rest of the sample
3. very unusual measurements from the same population

Measuring Speed (Variance Standard Deviation)

• to describe the spread or variation of a data set

• As shown above you must label which data set has which mean.  If you do not do this then you will not know which data set you are talking about.
• The measures of center (mean and median) cannot completely characterize a data set.  In fact, data set Y varies more than data set X does.
• ¿How can we measure the variation or dispersion of a data set?  Answer: by the sample range. Sample range = largest observation to the smallest observation
• Defect: (sometimes there are a lot of data points) It involves only 2 observations and disregards the rest (it is a waste of information)
• Deviation = Xi - (x-bar)

*end of Sept. 11, back top of the page*