Considering the curves  z in Fig. 3, we see
that in the near of "lengthened" antenna d z in Fig. 3, we see
that in the near of "lengthened" antenna d z /dr z /dr 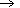 0 , so that here v 0 , so that here v
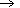 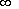 ; for the
"shortened" antennas d ; for the
"shortened" antennas d z /dr goes through the
minimum so that v has here the maximal value. Further, with the
increasing distance, v falls, and at r z /dr goes through the
minimum so that v has here the maximal value. Further, with the
increasing distance, v falls, and at r 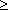 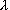 in
order to calculate v we have to use already the formula (20). Then
the value v becomes less than c/n and
reaches the minimal value which is the smaller (at f = const) the less the
conductance in
order to calculate v we have to use already the formula (20). Then
the value v becomes less than c/n and
reaches the minimal value which is the smaller (at f = const) the less the
conductance 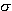 is. After it, v increases
monotonously, tending to the constant limit c/n [19]. This
result is practically important. It demonstrates that the radio waves dispersion over the
earth surface is negligibly small, and irrespectively of its electric properties, the
phase velocity at quite large distances from the radiator tends to the radio waves
velocity in the air" [18]. The results of measurement of the differential phase
velocity of radio waves at is. After it, v increases
monotonously, tending to the constant limit c/n [19]. This
result is practically important. It demonstrates that the radio waves dispersion over the
earth surface is negligibly small, and irrespectively of its electric properties, the
phase velocity at quite large distances from the radiator tends to the radio waves
velocity in the air" [18]. The results of measurement of the differential phase
velocity of radio waves at 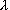 = 120, 180 m are shown in Fig. 4. = 120, 180 m are shown in Fig. 4. |
To compare the pattern of velocity variation in EM and
acoustic fields, in Fig. 5 we present the experimental regularity of the phase velocity
against the distance for the acoustic transversal wave from [15, Fig. 8]. We see in these
plots that in both fields immediately near the radiator the phase velocity is large and
fast falls with the distance. Having transited the minimum, the velocity grows, and in
limits (8 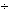 10) 10)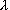 the near field is over. In the far field the propagation velocity tends to the
steady-state value. The difference in the depth of minimum is most likely caused by the
fact that in the acoustic experiment the acoustic conductance of the base has been
intentionally diminished as possible, to prevent the parasitic reflection of signal from
the surface. This caused both a small value of minimum and some growth of the near field,
in comparison with the EM field being the analogue.
the near field is over. In the far field the propagation velocity tends to the
steady-state value. The difference in the depth of minimum is most likely caused by the
fact that in the acoustic experiment the acoustic conductance of the base has been
intentionally diminished as possible, to prevent the parasitic reflection of signal from
the surface. This caused both a small value of minimum and some growth of the near field,
in comparison with the EM field being the analogue. |