In Fig. 12 we see the amplitude-frequency
characteristic of the longitudinal and transversal components of the wave in an elastic
line before the bend, with respect to 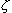 . At . At 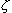 = 1 (the nearest curve in the plot) the
amplitude-frequency characteristic has a hyperbolic form usual for ideal lines. With
growing = 1 (the nearest curve in the plot) the
amplitude-frequency characteristic has a hyperbolic form usual for ideal lines. With
growing 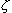 the
resonance peaks arise in the plots; their amplitude grows with growing the
resonance peaks arise in the plots; their amplitude grows with growing 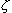 which can cause
the local destructions on the quite stable general background. Some peaks in the middle
band arise only at large values which can cause
the local destructions on the quite stable general background. Some peaks in the middle
band arise only at large values 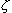 ; with growing ; with growing 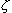 some peaks amplitude first grows, then
smoothes. The transversal component peaks become displaced with growing some peaks amplitude first grows, then
smoothes. The transversal component peaks become displaced with growing 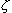 . This is caused
by growing . This is caused
by growing 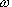 tr according to (32). It is
typical that despite the ideal pattern of elastic constraints the resonance peaks
amplitudes are finite. The peaks location for the longitudinal and transversal components
do not coincide too. In this connection, in such lines dependently on frequency either
longitudinal or transversal vibrations can prevail. Thus, in the propagation of a wave
having complex and especially continuous spectrum typical for solitary seismic waves, the
essential transformation of the wave shape takes place. A number of frequencies are
quenched in the wave travelling, and at the number of frequencies corresponding to the
resonance peaks the vibration amplitude abruptly increases; this process is not
synchronous for the longitudinal and transversal components. The smearing of the wave
packet caused by dependence of the phase delay (of the propagation velocity in that
number) on frequency adds to this. And taking into account that in the before-bend region
a complex superposition of standing and progressive waves takes place, the velocity
dispersion nonlinearly depends on the external excitation frequency. tr according to (32). It is
typical that despite the ideal pattern of elastic constraints the resonance peaks
amplitudes are finite. The peaks location for the longitudinal and transversal components
do not coincide too. In this connection, in such lines dependently on frequency either
longitudinal or transversal vibrations can prevail. Thus, in the propagation of a wave
having complex and especially continuous spectrum typical for solitary seismic waves, the
essential transformation of the wave shape takes place. A number of frequencies are
quenched in the wave travelling, and at the number of frequencies corresponding to the
resonance peaks the vibration amplitude abruptly increases; this process is not
synchronous for the longitudinal and transversal components. The smearing of the wave
packet caused by dependence of the phase delay (of the propagation velocity in that
number) on frequency adds to this. And taking into account that in the before-bend region
a complex superposition of standing and progressive waves takes place, the velocity
dispersion nonlinearly depends on the external excitation frequency. |
For the amplitude-frequency characteristic with respect to the bend
angle of an elastic line, we observe the similar pattern whose plots for the longitudinal
and transversal components in the before-bend region are shown in Fig. 13. With 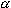 = 0 (the
curve in the middle part of the diagram) the amplitude-frequency characteristic has a
standard for an ideal line hyperbolic form even with = 0 (the
curve in the middle part of the diagram) the amplitude-frequency characteristic has a
standard for an ideal line hyperbolic form even with 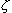 > 1. With growing > 1. With growing 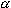 on the amplitude-frequency
characteristic there arise the resonance peaks whose amplitude increases with growing on the amplitude-frequency
characteristic there arise the resonance peaks whose amplitude increases with growing 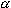 , and their
pattern depends not only on the value but also on the sign of , and their
pattern depends not only on the value but also on the sign of 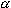 . As applied to
the seismic processes, it means that the abrupter transition from the flat country to the
mountains is, and the abrupter the curvature of a mountain arc is (the Pamir knot is a
typical example), the more destructive the earthquake consequences are. The same as in
Fig. 12, the velocity of amplitude growing is different for different peaks. Some peaks
reveal only at large values . As applied to
the seismic processes, it means that the abrupter transition from the flat country to the
mountains is, and the abrupter the curvature of a mountain arc is (the Pamir knot is a
typical example), the more destructive the earthquake consequences are. The same as in
Fig. 12, the velocity of amplitude growing is different for different peaks. Some peaks
reveal only at large values 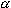 , with growing , with growing 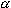 the low-frequency peak in Fig. 13 b
coalesces with the next resonance peak, and the peaks location on the amplitude-frequency
characteristic of the longitudinal and transversal components does not coincide. the low-frequency peak in Fig. 13 b
coalesces with the next resonance peak, and the peaks location on the amplitude-frequency
characteristic of the longitudinal and transversal components does not coincide. |