[]  IowaZ Sitemap [] Send Email []  FZ1 Owner's Association  []  IowaZ Vmax Sitemap  []  IowaZ V65 Magna Page  []

Use the FZ1 Sitemap  to navigate all of the FZ pages.

Yamaha FZ1
Explanation of Torque and Horsepower
 FZ1 Dyno Results
and other information on performance.

Rob will give you a print out of the torque, horsepower curves and 
give you an opinion on the  present state of the engine, exhaust, fuel systems,
and some helpful hints to make the bike run better or to increase power.

Input, information, posts regarding FZ dyno runs:
....If you have have made an FZ dyno run and would like to list the results for others use, post to me, iowaz@swbell.net 

Dyno Results and Posts:
....IowaZ FZ and two other FZ's on Rob's dyno, all three 120+ hp, 70+ ft-lb.  R1's are 134-136 on this dyno. My Max was 112 & 76, my V65 98 & 65.

....Jean's FZ from Austrailia---- 125 hp, 72 ft-lb.  R-1's are 130 on the same dyno, and some FZ's are approaching that value.  ??Are U.S.FZ's restricted??

.....jmness's FZ----Don't know about full system and jet kit but I got 120.9 HP yesterday on the dyno and then put on a Yosh RS-3 slip-on and ended up with a better sound and 123.4 HP. No holes in the power band, carburetion was right on.

....Rabett's FZ---I posted a photo of the dyno run done on my bike a week or two ago. HP was up around 128, torque at 74. Who knows how accurate these are.

....modette observed---A stock FZ1 made if I recall right at 119HP

Some Performance Data on various bikes:

Top Speeds:
....192mph, Suzuki Hayabusa (Oct 2001 Sport Rider)
....190mph, Kawasaki ZX-12R (Oct 2001 Sport Rider)
....179mph, Suzuki GSX-R1000 (Nov 2001 Sport Rider)
....157mph, Suzuki GSX-R600 (Nov 2001 Sport Rider)
....157mph, Honda CBR600F4i (Nov 2001 Sport Rider)
....157mph, Yamaha YZF-R6 (Nov 2001 Sport Rider)
....153mph, Yamaha FZ1 (Mag Reviews, Z's Sigma calc.)
....144mph, Yamaha Vmax (introduced 1985, Z's best guess)
....142mph, Honda 1985 V65 Magna (Z's best guess)
.....

Rear Wheel Hp
....159.8hp, Kawasaki ZX-12R (Oct 2001 Sport Rider)
....158.0hp, Suzuki Hayabusa (Oct 2001 Sport Rider)
....143.9hp, Suzuki GSX-R1000 (Nov 2001 Sport Rider)
....129.2hp, Honda CBR929RR (Nov 2001 Sport Rider)
....128.4hp, Yamaha YZF-R1 (Nov 2001 Sport Rider)
....120+hp, Yamaha FZ1 (Mag Reviews, Z's dyno run)
....108+hp, Yamaha Vmax (introduced 1985, Z's dyno run)
....101+hp, Suzuki Bandit 1200S (Oct 2000, Motorcyclist)
....100.1hp, Suzuki GSX-R600 (Nov 2001 Sport Rider)
.....98.6hp, Honda 1985 V65 Magna (Z's dyno run)
.....98.4hp, Honda CBR600F4i (Nov 2001 Sport Rider)
.....96.9hp, Yamaha YZF-R6 (Nov 2001 Sport Rider)
.....81.6hp, Moto Guzzi V11 Sport (Oct 2000, Motorcyclist)
Torque
...100.1ft-lb, Susuke Haybusa (Oct 2001 Sport Rider)
....91.4ft-lb, Kawasaki ZX-12R (Oct 2001 Sport Rider)
....77+ft-lb, Yamaha Vmax (introduced 1985, Z's dyno run)
....75.1ft-lb, Suzuki GSX-R1000 (Nov 2001 Sport Rider)
....71.8ft-lb, Suzuki Bandit 1200S (Oct 2000, Motorcyclist)
....70.3ft-lb, Yamaha YZF-R1 (Nov 2001 Sport Rider)
....70+ft-lb, Yamaha FZ1 (Mag Review, Z's dyno run)
....68+ft-lb, Honda V65 1985 Magna (Z's dyno run)
....67.6ft-lb, Honda CBR929RR (Nov 2001 Sport Rider)
....65.0ft-lb, Moto Guzzi V11 Sport (Oct 2000, Motorcyclist)
....45.2ft-lb, Suzuki GSX-R600 (Nov 2001 Sport Rider)
....43.6, Honda CBR600F4i (Nov 2001 Sport Rider)
....42.0, Yamaha YZF-R6

IowaZ Simplified Analogy of Torque, Horsepower and what it means on the Street.....
....In another life I once taught physics and physical science and approached this topic from a lab standpoint.  Now as the most basic of shade tree mechanics,  my interest is understanding torque and horsepower in an attempt to make order out of all the confusion coming from reading periodical reviews and various list posts regarding how this bike or that bike will out perform, out torque, out horsepower the others.  So what the #ell does it all mean??????

Off to Kinderphysics we go.....
We learn new words in Kinderphysics----Force, Work, Torque, Horsepower.
....For us, Force is energy exerted against matter.  We want to move something. That is pretty much how we can think of force.  We want the engine to generate force which can be applied to rotate the rear tire and drive us down the road.  

....Work is a force applied for "awhile." A force applied through a unit of time like a second, minute or hour. The force actually moves an object of interest, thus a force to move a pound one foot (assuming no friction) is the foot-pound, or ft-lb.  Ft-lb sounds familiar, it is work that sends the FZ scooting down the road.  It is also the turning force we apply to fasteners when we are wrenching on the FZ.  We are interested in just how much force that little-bitty inline four can apply to the ground through the tire, to propel us further and faster than all the other "land planes."

.....The word torque in the science of Physics refers to rotary force that does work  turning/spinning a machine.  If you run out of gas and are going to get your FZ off the road you could apply a force by hand in two different way to move the bike.   If you just stand behind and push, the force is linear or straight line force.  But if the tire is stuck in the mud and linear pushing is not working, you might try to grab and spin the back wheel forward to get the bike moving.  You are actually trying to rotate the wheel around the axle which in turn will move the bike forward out of the mud.  This rotational force you are applying is by  definition called torque.  Now you are a feeble torque producer at spinning the wheel, but that son of R1 engine is not, nor are most modern bikes.  They can produce a lot of force or torque to spin the rear wheel and accelerated the bike forward.

....In review, torque is a rather simple term to visualize.  It is force applied to rotate something like a pulley, a wheel, an axle.  Torque is a force, thus it is measured in ft-lb.  The amount of rotary force or torque that can be applied at any point in time is of interest to cyclist as if all things being equal it will give a feel of how "fast" a cycle can be accelerated forward.

.....Ask yourself which weight lifter can spin a merry-go-round faster, the super strong or the 98lb weakling??  That pretty well summarizes the torque issue.  Engines have varying abilities to apply rotation to their axels, shafts, pulleys, chains, wheels. Engines also produce different levels of torque at different times, and hold torque levels for varying times. 

.....A dynomometer is an instrument or machine that measures torque (ability to do rotary work).  Thus the word "dyno" that is thrown around in the cycling world.  Ft-lb's of torque applied per second can/is converted into a horsepower value for a specific engine at a specific rpm level.  The ability of an engine to produce rotary power or work varies within the rpm curve for that engine.

Hey Coach, keep the plays simple for us, will you!!  
..... You have just made a dyno run with your bike and are looking at the graph but what does it mean.  An oversimplified but effective visualization is to look at the top levels of the  torque curve as the point where the big strong weight lifter can really push or accelerate you down the road the quickest.  The low points of the curve have the 98 pounder pushing.  Or in the case of some bikes, a 98 pounder is always pushing.

....Another thing of interest is that a torque curve which is high at the higher rpm's means that we have a big strong weight lifter pushing but he is also a major sprinter, so he can respond very quickly to accelerate the #ell out of the bike while the bike is already at high speeds.  That kind of tells why a bike like the FZ or Max can be running along at 90-120 and still give the seat-of-the-pants the feel of dropping over the top of a roller coaster when the throttle is hit.  

....A cycle rider is basically interested in the torque of his bike engine or how much force the motor can apply to the road through the rotation of the various parts of the cycle drive train, as this is what he feel and uses to accelerate to a higher speed.  He is interested in how big and strong the weight lifter is and how quick the lifter can apply his power.  We like big explosive lifters.  But a word of caution in this analogy, size does not always matter in the torque game, as little lifters can be much stronger and more explosive than big boys.  It all depends on genetics and training.  Did coach mention to us,  R1 the "daddy" of the FZ engine, or Venture the uncle of the Max V4?  And what about the training at the race track for the FZ's daddy and on the highway for the uncle of Mr. Max.  Then again, you can see what can happen with children.  You can be a genetic stud like the Vmax or you can be a drooler like the Royal Star.  Thank heaven thoroughbred's like the R1 almost always have race level offspring, or we can be sure some spandex boy at Damaha would detune it to drooler class because, "That is what the want."  Ya, sure!

....Another thing the average street rider must consider when bragging about the torque or power of his "athlete" is that, often the big slow boys can produce the big torque and acceleration off the line at low/slow rpms.  The lineman can knock the crap out of the back in front of him, but let the back get into open field where his power and speed will produce the "torque" of acceleration and the lineman has no chance of catching up.  The lineman may be able to run nearly the same top speed at the start but will never catch up because upon every acceleration point the big boy will fall farther and farther behind in the race to the goal.  Some guys are muscle boys and have it all.  The linebackers are big, strong, agile and fast.  So are real and modern muscle bikes capable of high rpm's with big long, powerful torque and horsepower curves.

....Actual work output of an engine or horsepower will continue to climb as the rpms go up as long as the rpm's can be maintained.  Once the big guy is moving it does not take as much force or torque to keep him moving, thus as the engine spins faster more work is done, or more horsepower output.  Visualize again----torque is the big fast lifter pushing, accelerating  you hard down the road, while horsepower is just the overall work being done or how fast the big guy is getting down the road.  Once he is in motion at any given speed it does not take as much to keep him motivating along so his total work or horsepower is going up the faster his big legs rotate.

.....Harley's and Rice brand cruisers tend to produce a lot of torque/force at lower rpm's.  Their riders like that as they ride relatively slow around town or accelerate from low speeds.  For more aggressive and experienced riders it is better to have high torque at middle and high rpm's.  Most of the street time on bikes like the FZ is spent at 3-7k rpm's, that is why you read about the mid-range of street bikes.  It is the middle of the rpm range where good torque/force is desired for street riding.  They are the big strong athletes with fantastic sprint speed who can dart left and right, has power, speed and gears.  He is the linebacker, the stud :)  He is the bike that is good from light to light and at highway roll-ons.  He is the bike that can literally do it all during the street game.  

.....The rule for the non-cruiser type but non-racer type, the street hooligan,  is to have a lot of torque in the mid range of the rpm curve.  Most inline four or V-four street riders of bikes, like the old muscle bikes and standards, and now the  Super Standards including the FZ,  keep their rpm's from 3000 to about 7000 during most of their riding time.  It is at these rpm's we want high torque in all gears (a big bad fast athlete who can dart).  It is in this range that the Muscle Standards dominate the everyday street.  The high low-end-torque of the Hardley/cruiser crowd can not compete off the line with this kind of torque at high rpms. They often can come off as fast or faster but just run out of "steam" too soon.  Now do not take the low end torque of a Hardley lightly, as they are torque machines for a short distant off the line, everything else being equal.  Weight, gearing, engine efficiency, etc.   Hardley's can be the real deal at the low end of the rpm range.  So despite my Harley bashing, which is really all in fun, a good Harley rider, a rider much better than we are,  with some engine work, is a powerful street rider and will probably blow you socks off.

.....For aggressive/fun all round street riding, the rule is to have high torque at the mid-range of the rpm curve and to have the torque or power output continue well into the high rpm's.  Thus the Super Standards from any company and the old Muscle Bikes dominate the "streets."  Are we biased :))  Actually it is generally the rider and not the bike that is the dominator.

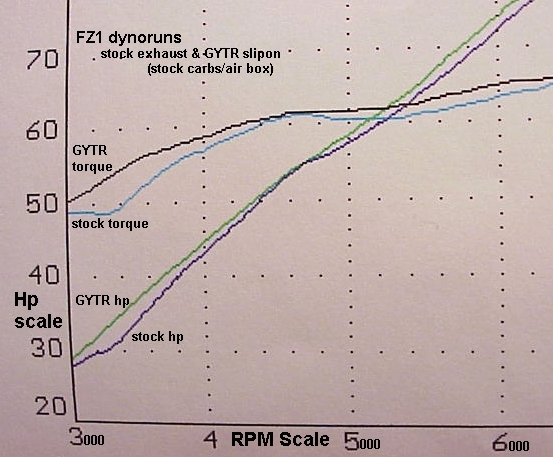
....When you take a look at the FZ torque/hp curves below you will notice that torque stays high from about 3k to the end of the power band, and  horsepower just keeps climbing. Between 5 and 10+ k rpms the FZ torque (rotary force) is at its best. Thus the reason why the FZ will just keep "coming on" until redline.  Torque peak seems to be about 70 ft-lb for the FZ. which is in the high range, especially for a 1000 cc street engine, with the relatively light weight and a horsepower curve that continues to the end of the rpm's.results.  

....There are quite a number of other bikes on the street producing torque in the 80's and 90's stock but most are heavy and cannot turn high rpm's and produce high hp.  It would appear that most stock FZ's are right at 120 +/- hp.  and  70 +/- ft-lb of torque.  

....Three FZ's have been run on this specific dyno with the same relative results:  120+ hp, 70+ torque.

Rob Creighton of Performance Diagnostics out of Cedar Rapids, Iowa does hundreds of dyno runs on all types of cycles,  all over the midwest and is capable of immediate analysis and suggestions on tuning. He is a master Harley tuner, as an example being able to take an 883 Sportster from about 43-45 hp to 93 +/- hp with about $2500 in mods and time, which is major bang for the buck.  http://www.performancediagnostics.com  As with most of us, Rob likes all types of bikes.

Rich, the owner of Midwest Performance, http://.www.midwestperformacne.com  , good shop/good service.  in Keokuk, Iowa, heading out for a test ride on Z'FZ1 and to warm it up for a dyno run. Midwest Performance brings the dyno to Keokuk at the end of May and June each year.  Lucky for me I latched onto this FZ before Rich had a chance to ride it :))  Rich is a major cycle rider and knows a good thing!!  He will be on an FZ soon ;)  

Yamaha's GYTR Slipon

IowaZ's FZ1 dynorun comparisons:

Horsepower
....Stock exhaust = 120.1 hp
....GYTR slipon   =  122.2 hp

Torque
....Stock torque = 70.0 ft-lb
....GYTR slipon = 70.3 ft-lb

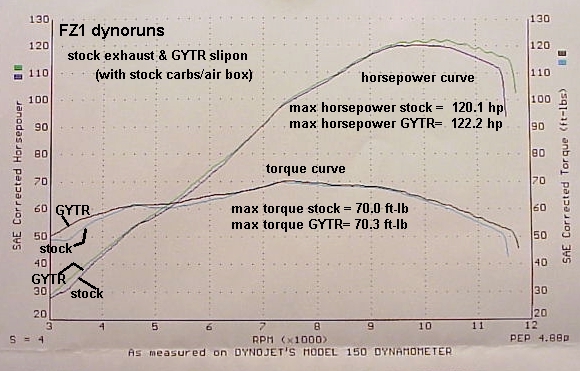
....My "seat of the pants" performance opinion of the GYTR slipon from Yamaha was good right from the start.  I could feel no low spots, hesitation, problems in any area of the RPM band.  The dynorun backs up the seat of the pants evaluation of the slipon.
....The dyno run of the GYTR slipon shows improved performance at low to midrange rpm's and smooths out both the hp and torque curves in the low range.
....At this point in time, I am more than happy with the hp/torque output of the FZ1 either stock or with the GYTR slipon.  It runs perfect from idle to top end.
....I will be running stock carbs and air box, and not joining the great tuning wars of rejetting, as this is more than enough "juice" to racetour and troll for Hardleys ;)

Some Other Posts and  Dyno Runs Reported by FZ riders

KSFZ1, Sept 29, 2001
....My first runs bone stock were 120 hp with 70 ft/lb of torque.
....I added Ivans Jet Kit and Yosh TRS Race slip-on exhaust and am getting 132.8 and 74.7 ft/lb. Not bad. I had a dyno run this afternoon. Here are the results.
SAE Max HP=132.8 @ 10500 rpm SAE Max Torque= 74.7 ft/lb The HP curve looks like a straight line through 9500 rpms then it rounds off. The Torque curve looks good too. Nice and fat. The Air/Fuel Ratio looks flat after 5200-5500 rpms Ratio = 13. But at 2800 rpm the AFR is 14 then dips dpwn tp 11.5 at 4000 rpms and comes back up to 13 at around 5200 to 5300 rpms. Looks like I am running rich in the needle jet circuit.

Feb 2001

Torque and Horsepower
....There's been a certain amount of discussion, in this and other files, about the concepts of horsepower and torque, how they relate to each other, and how they apply in terms of automobile performance. I have observed that, although nearly everyone participating has a passion for automobiles, there is a huge variance in knowledge. It's clear that a bunch of folks have strong opinions (about this topic, and other things), but that has generally led to more heat than light, if you get my drift :-). I've posted a subset of this note in another string, but felt it deserved to be dealt with as a separate topic. This is meant to be a primer on the subject, which may lead to serious discussion that fleshes out this and other subtopics that will inevitably need to be addressed.
....OK. Here's the deal, in moderately plain english.
....Force, Work and Time
If you have a one pound weight bolted to the floor, and try to lift it with one pound of force (or 10, or 50 pounds), you will have applied force and exerted energy, but no work will have been done. If you unbolt the weight, and apply a force sufficient to lift the weight one foot, then one foot pound of work will have been done. If that event takes a minute to accomplish, then you will be doing work at the rate of one foot pound per minute. If it takes one second to accomplish the task, then work will be done at the rate of 60 foot pounds per minute, and so on.
....In order to apply these measurements to automobiles and their performance (whether you're speaking of torque, horsepower, newton meters, watts, or any other terms), you need to address the three variables of force, work and time.
....Awhile back, a gentleman by the name of Watt (the same gent who did all that neat stuff with steam engines) made some observations, and concluded that the average horse of the time could lift a 550 pound weight one foot in one second, thereby performing work at the rate of 550 foot pounds per second, or 33,000 foot pounds per minute, for an eight hour shift, more or less. He then published those observations, and stated that 33,000 foot pounds per minute of work was equivalent to the power of one horse, or, one horsepower.
.]..Everybody else said OK. :-)
....For purposes of this discussion, we need to measure units of force from rotating objects such as crankshafts, so we'll use terms which define a *twisting* force, such as foot pounds of torque. A foot pound of torque is the twisting force necessary to support a one pound weight on a weightless horizontal bar, one foot from the fulcrum.
....Now, it's important to understand that nobody on the planet ever actually measures horsepower from a running engine. What we actually measure (on a dynomometer) is torque, expressed in foot pounds (in the U.S.), and then we *calculate* actual horsepower by converting the twisting force of torque into the work units of horsepower.
....Visualize that one pound weight we mentioned, one foot from the fulcrum on its weightless bar. If we rotate that weight for one full revolution against a one pound resistance, we have moved it a total of 6.2832 feet (Pi * a two foot circle), and, incidently, we have done 6.2832 foot pounds of work.
....OK. Remember Watt? He said that 33,000 foot pounds of work per minute was equivalent to one horsepower. If we divide the 6.2832 foot pounds of work we've done per revolution of that weight into 33,000 foot pounds, we come up with the fact that one foot pound of torque at 5252 rpm is equal to 33,000 foot pounds per minute of work, and is the equivalent of one horsepower. If we only move that weight at the rate of 2626 rpm, it's the equivalent of 1/2 horsepower (16,500 foot pounds per minute), and so on. Therefore, the following formula applies for calculating horsepower from a torque measurement:
....Torque * RPM
Horsepower = ------------
5252
This is not a debatable item. It's the way it's done. Period.
....The Case For Torque
Now, what does all this mean in carland?
....First of all, from a driver's perspective, torque, to use the vernacular, RULES :-). Any given car, in any given gear, will accelerate at a rate that *exactly* matches its torque curve (allowing for increased air and rolling resistance as speeds climb). Another way of saying this is that a car will accelerate hardest at its torque peak in any given gear, and will not accelerate as hard below that peak, or above it. Torque is the only thing that a driver feels, and horsepower is just sort of an esoteric measurement in that context. 300 foot pounds of torque will accelerate you just as hard at 2000 rpm as it would if you were making that torque at 4000 rpm in the same gear, yet, per the formula, the horsepower would be *double* at 4000 rpm. Therefore, horsepower isn't particularly meaningful from a driver's perspective, and the two numbers only get friendly at 5252 rpm, where horsepower and torque always come out the same.
....In contrast to a torque curve (and the matching pushback into your seat), horsepower rises rapidly with rpm, especially when torque values are also climbing. Horsepower will continue to climb, however, until well past the torque peak, and will continue to rise as engine speed climbs, until the torque curve really begins to plummet, faster than engine rpm is rising. However, as I said, horsepower has nothing to do with what a driver *feels*.
....You don't believe all this?
Fine. Take your non turbo car (turbo lag muddles the results) to its torque peak in first gear, and punch it. Notice the belt in the back? Now take it to the power peak, and punch it. Notice that the belt in the back is a bit weaker? Fine. Can we go on, now? :-)
....The Case For Horsepower
OK. If torque is so all-fired important, why do we care about horsepower?
....Because (to quote a friend), "It is better to make torque at high rpm than at low rpm, because you can take advantage of *gearing*.
....For an extreme example of this, I'll leave carland for a moment, and describe a waterwheel I got to watch awhile ago. This was a pretty massive wheel (built a couple of hundred years ago), rotating lazily on a shaft which was connected to the works inside a flour mill. Working some things out from what the people in the mill said, I was able to determine that the wheel typically generated about 2600(!) foot pounds of torque. I had clocked its speed, and determined that it was rotating at about 12 rpm. If we hooked that wheel to, say, the drivewheels of a car, that car would go from zero to twelve rpm in a flash, and the waterwheel would hardly notice :-).
...On the other hand, twelve rpm of the drivewheels is around one mph for the average car, and, in order to go faster, we'd need to gear it up. To get to 60 mph would require gearing the wheel up enough so that it would be effectively making a little over 43 foot pounds of torque at the output, which is not only a relatively small amount, it's less than what the average car would need in order to actually get to 60. Applying the conversion formula gives us the facts on this. Twelve times twenty six hundred, over five thousand two hundred fifty two gives us: 6 HP.
....Oops. Now we see the rest of the story. While it's clearly true that the water wheel can exert a *bunch* of force, its *power* (ability to do work over time) is severely limited.
....At The Dragstrip
OK. Back to carland, and some examples of how horsepower makes a major difference in how fast a car can accelerate, in spite of what torque on your backside tells you :-).
....A very good example would be to compare the current LT1 Corvette with the last of the L98 Vettes, built in 1991. Figures as follows:
....Engine Peak HP @ RPM Peak Torque @ RPM
------ ------------- -----------------
L98 250 @ 4000 340 @ 3200
LT1 300 @ 5000 340 @ 3600
The cars are geared identically, and car weights are within a few pounds, so it's a good comparison.
.... as fast as the other to the driver, but the LT1 will actually be significantly faster than the L98, even though it won't pull any harder. If we mess about with the formula, we can begin to discover exactly *why* the LT1 is faster. Here's another slice at that formula:
....Horsepower * 5252
Torque = -----------------
....RPM
If we plug some numbers in, we can see that the L98 is making 328 foot pounds of torque at its power peak (250 hp @ 4000), and we can infer that it cannot be making any more than 263 pound feet of torque at 5000 rpm, or it would be making more than 250 hp at that engine speed, and would be so rated. In actuality, the L98 is probably making no more than around 210 pound feet or so at 5000 rpm, and anybody who owns one would shift it at around 46-4700 rpm, because more torque is available at the drive wheels in the next gear at that point.
....On the other hand, the LT1 is fairly happy making 315 pound feet at 5000 rpm, and is happy right up to its mid 5s redline.
....So, in a drag race, the cars would launch more or less together. The L98 might have a slight advantage due to its peak torque occuring a little earlier in the rev range, but that is debatable, since the LT1 has a wider, flatter curve (again pretty much by definition, looking at the figures). From somewhere in the mid range and up, however, the LT1 would begin to pull away. Where the L98 has to shift to second (and throw away torque multiplication for speed), the LT1 still has around another 1000 rpm to go in first, and thus begins to widen its lead, more and more as the speeds climb. As long as the revs are high, the LT1, by definition, has an advantage.
....Another example would be the LT1 against the ZR-1. Same deal, only in reverse. The ZR-1 actually pulls a little harder than the LT1, although its torque advantage is softened somewhat by its extra weight. The real advantage, however, is that the ZR-1 has another 1500 rpm in hand at the point where the LT1 has to shift.
...There are numerous examples of this phenomenon. The Integra GS-R, for instance, is faster than the garden variety Integra, not because it pulls particularly harder (it doesn't), but because it pulls *longer*. It doesn't feel particularly faster, but it is.
....A final example of this requires your imagination. Figure that we can tweak an LT1 engine so that it still makes peak torque of 340 foot pounds at 3600 rpm, but, instead of the curve dropping off to 315 pound feet at 5000, we extend the torque curve so much that it doesn't fall off to 315 pound feet until 15000 rpm. OK, so we'd need to have virtually all the moving parts made out of unobtanium :-), and some sort of turbocharging on demand that would make enough high-rpm boost to keep the curve from falling, but hey, bear with me.
....If you raced a stock LT1 with this car, they would launch together, but, somewhere around the 60 foot point, the stocker would begin to fade, and would have to grab second gear shortly thereafter. Not long after that, you'd see in your mirror that the stocker has grabbed third, and not too long after that, it would get fourth, but you'd wouldn't be able to see that due to the distance between you as you crossed the line, *still in first gear*, and pulling like crazy.
....I've got a computer simulation that models an LT1 Vette in a quarter mile pass, and it predicts a 13.38 second ET, at 104.5 mph. That's pretty close (actually a tiny bit conservative) to what a stock LT1 can do at 100% air density at a high traction drag strip, being powershifted. However, our modified car, while belting the driver in the back no harder than the stocker (at peak torque) does an 11.96, at 135.1 mph, all in first gear, of course. It doesn't pull any harder, but it sure as hell pulls longer :-). It's also making *900* hp, at 15,000 rpm.
....Of course, folks who are knowledgeable about drag racing are now openly snickering, because they've read the preceeding paragraph, and it occurs to them that any self respecting car that can get to 135 mph in a quarter mile will just naturally be doing this in less than ten seconds. Of course that's true, but I remind these same folks that any self-respecting engine that propels a Vette into the nines is also making a whole bunch more than 340 foot pounds of torque.
....That does bring up another point, though. Essentially, a more "real" Corvette running 135 mph in a quarter mile (maybe a mega big block) might be making 700-800 foot pounds of torque, and thus it would pull a whole bunch harder than my paper tiger would. It would need slicks and other modifications in order to turn that torque into forward motion, but it would also get from here to way over there a bunch quicker.
....On the other hand, as long as we're making quarter mile passes with fantasy engines, if we put a 10.35:1 final-drive gear (3.45 is stock) in our fantasy LT1, with slicks and other chassis mods, we'd be in the nines just as easily as the big block would, and thus save face :-). The mechanical advantage of such a nonsensical rear gear would allow our combination to pull just as hard as the big block, plus we'd get to do all that gear banging and such that real racers do, and finish in fourth gear, as God intends. :-)
....The only modification to the preceeding paragraph would be the polar moments of inertia (flywheel effect) argument brought about by such a stiff rear gear, and that argument is outside of the scope of this already massive document. Another time, maybe, if you can stand it :-).
....At The Bonneville Salt Flats
Looking at top speed, horsepower wins again, in the sense that making more torque at high rpm means you can use a stiffer gear for any given car speed, and thus have more effective torque *at the drive wheels*.
....Finally, operating at the power peak means you are doing the absolute best you can at any given car speed, measuring torque at the drive wheels. I know I said that acceleration follows the torque curve in any given gear, but if you factor in gearing vs car speed, the power peak is *it*. An example, yet again, of the LT1 Vette will illustrate this. If you take it up to its torque peak (3600 rpm) in a gear, it will generate some level of torque (340 foot pounds times whatever overall gearing) at the drive wheels, which is the best it will do in that gear (meaning, that's where it is pulling hardest in that gear).
....However, if you re-gear the car so it is operating at the power peak (5000 rpm) *at the same car speed*, it will deliver more torque to the drive wheels, because you'll need to gear it up by nearly 39% (5000/3600), while engine torque has only dropped by a little over 7% (315/340). You'll net a 29% gain in drive wheel torque at the power peak vs the torque peak, at a given car speed.
....Any other rpm (other than the power peak) at a given car speed will net you a lower torque value at the drive wheels. This would be true of any car on the planet, so, theoretical "best" top speed will always occur when a given vehicle is operating at its power peak.
...."Modernizing" The 18th Century
OK. For the final-final point (Really. I Promise.), what if we ditched that water wheel, and bolted an LT1 in its place? Now, no LT1 is going to be making over 2600 foot pounds of torque (except possibly for a single, glorious instant, running on nitromethane), but, assuming we needed 12 rpm for an input to the mill, we could run the LT1 at 5000 rpm (where it's making 315 foot pounds of torque), and gear it down to a 12 rpm output. Result? We'd have over *131,000* foot pounds of torque to play with. We could probably twist the whole flour mill around the input shaft, if we needed to :-).
....The Only Thing You Really Need to Know
Repeat after me. "It is better to make torque at high rpm than at low rpm, because you can take advantage of *gearing*." :-)

Use the FZ1 Sitemap  to navigate all of the FZ pages.

 []  IowaZ Sitemap [] Send Email []  FZ1 Owner's Association   []  IowaZ Vmax Sitemap  []  IowaZ V65 Magna Page  []

Any reproduction of this site or it's contents requires express written consent.