C. Spark Charts

Before the game starts, Imelda's reactions to Bob are set randomly. She may either blindly choose one of the twelve pre-printed Spark Charts and give it to Gorm without looking at it, or else Gorm can create one of the charts on a piece of paper. The Spark Chart shows which actions by the two humans will result in a Spark between them, which actions will bother Imelda, and which actions will have no result.

Use these links to view Spark Charts 1-6 and 7-12. Print and cut the twelve charts apart. Shuffle them before letting Imelda draw one, but don't let Imelda see it. Gorm will hang on to it until the end.

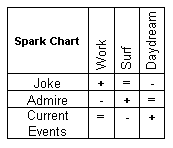To create your own Spark Chart on the spot, draw a Tic-Tac-Toe board. Start with a Plus-sign, Minus-sign or Equal sign in the top left space. The top row must use each of the symbols only once. Continue filling out the blank spaces of the chart so that rows across use each of the symbols only once and columns (up and down) use each of the symbols only once. Down the left side of your chart, label the rows Joke, Admire, Current Events. Across the top of the chart, label the columns Work, Surf and Daydream.

To find Imelda's reaction to Bob's pleas for attention, find the row of the chart corresponding with Bob's action and follow it across to the column corresponding with Imelda's action. A Plus means that Bob gains a Spark. Minus means that Bob loses a Spark (although he can't go below zero). Equal sign means Imelda ignored him, or didn't feel a spark.

During play, Gorm is responsible for recording each of the players' basic actions, and checking their results. The results should not be revealed until the end, except that the sponge ghost should point out the first time Bob makes Imelda smile. It's okay to make quick notes or abbreviations of the actions. For example if the first confrontation was Bob telling a Joke while Imelda Works, resulting in a Spark, you could write "1. J/W +" or any way you want to note the actions and results, as long as you remember what your notes mean later.