Learning LT Spice.
Lesson 5

Table of Contents.

Lesson 1: Creating a net list and a Simple Simulation.
Lesson 2: Introduction to and applications of frequency analysis.
Lesson 3: Introduction to and applications of transient analysis.
Lesson 4: Locating, modifying, and installing vacuum tube models.
Lesson 5: Operating point of vacuum tube circuits. Introduction to stepping and plate curves. This Page.
Lesson 6: Using stepping to do frequency response of a tone control.
Lesson 7: Transient analysis of unregulated power supplies.
Lesson 8: Transient analysis of power supply regulators.
Lesson 9: Transient and frequency analysis of amplifiers with feedback.
Lesson 10: Lossless transformers.

What you will learn in Lesson five. How to:

1. Determine the DC operating point of the tube in a resistance coupled amplifier.
2. Run the frequency response of the R C amplifier.
3. Find the Vout / Vin gain of the R C amplifier.
4. Examine how changing the value of the coupling capacitor effects low end frequency response.
5. Examine how adding a cathode bypass capacitor increases the gain and its effect on the low end.
6. Compare an R C amplifier with different tube types plugged in.
7. Build a simulated curve tracer for plate characteristics
8. Measuring rp, Gm, and μ, of a tube model and comparing them with tube manual values.
9. Avoid misinterpretation of results through use of two RLC filter circuits.

Things That are very Hard to Remember.

That step by step procedure given in lesson one has been placed in a text file which can be downloaded by holding the control key while pressing enter on the link.
On my computer the file opens as if it were a webpage. Control enter on the link will open the file in a separate window. That way you can refer to it without closing the lesson page. Control tab will switch between the two windows.

Here is more information you can look up because it is so hard to remember. Control enter on this link for the same reason as above.

A note on total and partial.

At the start I designed this page to be usable by a totally blind person. As it evolved I decided to leave some of the figures in place for the benefit of any partially blind who may also be viewing it. When possible I have kept everything blind accessible but the pictures are there for anyone who might benefit from them. For some of the subjects which were covered on the sighted page I was unable to make translations for the blind. I just couldn't think of a way.

Verbal description of Figure 5.1.

A generator V1 is labeled AC 1 and has its negative end grounded. The positive end connects directly to the grid of XU1, 12 A X 7. The cathode of XU1 connects to a node labeled K1 and goes through R1, 3.3 k ohm to ground. The plate of XU1 goes to node P1 and also goes through a R2, 270 k ohm to the plus end of V2 250 volt. The negative end of V2 is grounded. A capacitor, C1, 0.01 u f, connects between nodes P1 and out. Node out goes through R3, a 470 k ohm resistor, to ground. End verbal description.

Save the circuit as slp-fig-05-01. Note that there are two nodes in the diagram, not counting ground, which were not given names or numbers in the verbal description. You will have to give these nodes names or numbers when you write your netlist, which you are going to do without help this time. Spice directives traditionally go at the end of the list so here they are.
.lib 12AX7.sub
.op
;.ac 3 1 1Meg
Note that the ac directive is deactivated by having a semicolon placed in front of it. Leave it this way as you type it in. Also the op directive remains active.

Determining the Operating Point.

Run the simulation. A list of node voltages and component currents appears in a popup box. You may have to argue with JAWS a bit to get the focus on it and get it read. I have never learned how to move the focus around in JAWS. When I ask someone how to do it they say incredulously, "You mean you don't know how to do that?" and they never tell me. So you are on your own with this one. Assuming you are smarter than I am when you read the list you will see that the listing includes V(p1) = 134.8 volts and V(k1) = 1.408 volts. I have rounded off these values. I haven't yet found a way to make LTspice round off the printed values. There may not be a way.

If you have time you might want to try different models to see if they yield different results.

Running the frequency response.

Edit the netlist and remove the semicolon from in front of the .ac directive to re enable it. There is no need to disable the op directive. Run the simulation. Export the data as a text file and read it with your favorite text file reader. You will find the gain in dB and phase angle to 15 significant digits.

Finding the V(out) / V(in) of the amplifier.

I don't know how to do this in a nonvisual way.
This is an area where the terminology gets a little fuzzy. What is shown above is the gain in dB. When engineers and technicians say "gain" they generally mean the output voltage divided by the input voltage. Because this is a voltage divided by a voltage it has no dimensions. It is not the gain in anything, it is just the gain. If you have a science and engineering calculator you can calculate the gain from gain in dB with just a few keystrokes. But if you don't have one and you are curious you might want to know how to make LTspice tell you.

Move the cursor over the graph area and click anywhere. Move it to the dB scale on the left. It will turn into a ruler. Right click and in the box that opens click the "linear" radio button then OK. LTspice is not particularly rigorous about units. This is actually the output voltage but we have set the input voltage at 1 volt by setting the magnitude of the generator. So the gain and output voltage are numerically equal.

C1 and Low End Frequency Response.

Edit your netlist and change the value of C1 from "0.01u" to "{C1}" These are called braces.
Right and left arrow over the new value for C1 so you clearly understand how to label the capacitor.
Add the following spice directive to your netlist.
.step param C1 0.01uf 0.022uf 0.047uf 0.1uf 0.22uf 0.47uf

Figure 5.4 Showing Simple One Stage Amplifier.

Note: Figure left in place.

Edit the .ac directive to read as follows.
.ac dec 3 1 100
This will set the number of samples per decade to 3 and set the frequency range from 1 to 100 Hz.

Looking at the gain values at 20 Hz it is clear that there is a small improvement by going from 0.047 uf to 0.1 uf. But it seems pointless to go above 0.1 uf. This is an example of the kinds of insights that LTspice can give you that you couldn't easily get from a breadboard.

Adding a cathode bypass capacitor.

Set the value of C1 to a fixed value of either 0.1 uf or 0.22 uf.
Add a cathode bypass capacitor from node K1 to ground. The added capacitor will be C2. Don't forget that the value of C2 must be {C2} and you need to change C1 to C2 in the ".step" directive. Edit the ".step" directive list to step C2 from 2.2 uf to 47 uf in a similar sequence to that used for C1.
If you set C1 to 0.1 uf set it to 0.22 uf and run the simulation again. If you initially set it to 0.22, set it to 0.1 uf and run it again. Note the gain values at 6 Hz.
If you feel the values of frequency in the table are not close enough to the values above try increasing the number of points. This is the number following "dec" in the ".ac" directive.
Since the plot only covers two decades you can easily afford to set this number to 6 or even 10.
Set the value of C2 to 22uf and C1 to 0.22uf.

Figure 5.5 Results of Stepping the cathode bypass capacitor with C1 at 0.22 uf.

Figure 5.6 Results of Stepping the cathode bypass capacitor with C1 at 0.1 uf.

Note: Two Figures left in place.

What Happens if you Plug in a Different Tube.

This is a question often asked by the uninitiated. They are told "in general don't do it. You could do damage to the tube or device you are plugging it into or both." But in the case of the 12 volt dual triodes you can plug away as long as it doesn't have series strung heaters. The operating point might be a little off but it often doesn't matter.

So let's clone the netlist for our little amplifier circuit and see what damage we can do. First we need to decide what part to clone.
We want to clone R1, R2, R3, C1, C2, and XU1
It is hoped that these 6 components are all on contiguous lines. If not you need to do a little cutting and pasting to get them together.
Copy the six lines by selecting them and pressing ctrl-C and then be sure the cursor is after the last line of the 6.
Then press ctrl-V three times.
You are a long way from being done. You need to change all the numbers that are duplicated.
Say you have components in the following order, R1, R2, R3, C1, C2, and XU1.
In the next group they need to read R4, R5, R6, C3, C4, and XU2.
Get the idea? Change the remaining two groups. Think you are done? Think again.
You have nodes named K1, P1, and out in all four groups. In spice where ever multiple nodes have the same name they are electrically connected together. You don't want all the cathodes connected together all the plates and all the outputs. So the cathode and plate of XU2 should connect to K2 and P2 etc.
C1 should connect between nodes P1 and out1. C3 between P2 and out2 etc.
Double check this very carefully. If this is not done correctly the circuit will not perform as intended.
Now you need to add ".lib" directives for 6CG7, 12 A T 7, without the spaces, and 12BH7.
And you need to change the value of Xu2, Xu3 and XU4 to 12AT7, 12bh7, and 6CG7. You don't have to use these tubes. You can use any triodes you are curious about.

Figure 5.9 Showing Four Complete Independent Amplifiers.

Note: Figure left in place.

Checking the operating point isn't hard, just edit the ".ac" directive and type a semicolon in front of it. Then run the simulation. The results will be in a popup box as before. They all are pretty good but the plate voltage of the 12BH7 might be a little on the low side. I'm not going to tell you what it is. You will have to run it yourself to find out. The same goes for the AC results.

Wish I had chosen another tube or tubes? You've got the models. You don't need my permission to run them. That's what LTspice is all about.

Characteristic Plate Curves. Just Like the Tube Manual.

Based on what you have learned to date you are probably thinking of using the ".step" directive to step a couple of DC voltage sources. But that one doesn't give us the graph we want. The directive that works here is ".DC". It will cause the voltage of one of the sources to be plotted versus another DC value such as a voltage or current. Thus, we can wind up with the classic plate characteristic family of curves.

Here's where to start.

Figure 5.10 Showing the Tube Curves Circuit.

Note: Figure left in place.

Verbal description of Figure 5.10.

On the left is a generator, V2, 0 volts. The negative end of V2 is grounded while the positive end connects to the grid of a triode tube, XU1, a 12AU7. The cathode of XU1 is grounded. The plate connects to the positive of generator V1, 0 volts. The negative is grounded. A spice directive on the diagram reads ".lib 12AU7.sub". Another directive reads ".dc V1 0 500 50 V2 0 -25 5". A comment reads "Plate characteristic curves". End verbal description.

So you think I must have screwed up by putting V2 on the left and V1 on the right. Wrong. If, when you write your netlist you decide to fix my mistake by reversing V1 and V2 you will find that it doesn't work as predicted. Leave it as described. Here is what spice does in response to the .dc directive. V2 is set to zero volts and held there while V1 steps from 0 to 500 volts. Then V2 is set to -5 volts and V1 is once again stepped from 0 to 500 volts. The value of V1 appears on the X axis of the visual graph and the user can select what is plotted on the Y axis. To get the desired curves the user must select the plate current of XU1. A sighted user will set up V1 to change in 0.5 volt steps which would generate a lot of printed data. We have chosen V1 steps of 50 volts to keep the amount of data within reason.

The item you want to select to be plotted on the Y axis is IX(u1:A) which means the anode current of XU1.
This works well. The data are presented in two columns. First is the plate (anode) voltage and second is the plate current. Eleven rows takes the plate voltage from zero to 500 volts in steps of 50 volts. Above the first group is the legend V2 = 0 volts. The second group down the page has the legend V2 = -5 volts and again goes from V1 =0 to 500. You can see that the plate current for a given plate voltage becomes les and les as the grid is set more negative.

It is possible to modify things a bit to obtain all of the tube parameters, "Amplification Factor", "Transconductance", and "Plate Resistance".

Plate Resistance.

We are doing this one first because it takes the least amount of modification of the circuit. From the Sylvania tube manual,
Plate voltage = 100 Volts,
Grid voltage = 0
Plate current = 11.8 mA.
Plate resistance = 6500 ohms.
Transconductance = 3100 μmhos.
Amplification Factor = 20.

Plate voltage =250 Volts,
Grid voltage = -8.5 Volts,
Plate current = 10.5 mA.
Plate resistance = 7700 ohms.
Transconductance = 2200 μmhos.
Amplification Factor = 17.

The definition of plate resistance is the change in plate voltage / change in plate current, with grid voltage held constant.

Figure 5.12 Showing Plate curves with cursors and readout box.

Edit the .dc spice directive as follows. Type a semicolon just before V2. Change the steps on V1 to go from 95 to 105 volts in a single 10 volt step. It should read,
".dc V1 95 105 10 ;V2 0 -25 5".

The file now has only two points. V1 = 95 volts, Ip = 10.975 mA and V1 = 105 volts, Ip = 12.454 mA. Now you need a calculator. The formula is,

rp = (Vhi - Vlo) / (Ihi - Ilo).

The value I calculate is 6.76 k ohms.
As compared to 6.5 k ohms that's an error of 4.02%.
Even in the golden age of tubes an error in tube parameters of 5% was considered to be very good. My measurements indicate that among tubes being made now there is considerably more variation than that among tubes of the same type number.

Now change the directive to this. ".dc V1 245 255 10 ;V2 0 -25 5".
Change the value of V2 from 0 to -8.5.
From this run I get rp = 7.68 k ohms. Percent error = -0.25%.
That probably says a lot about the tube model being used.

Transconductance.

Plate voltage = 100 Volts,
Grid voltage = 0
Plate current = 11.8 mA.
Plate resistance = 6500 ohms.
Transconductance = 3100 μmhos.
Amplification Factor = 20.

Plate voltage =250 Volts,
Grid voltage = -8.5 Volts,
Plate current = 10.5 mA.
Plate resistance = 7700 ohms.
Transconductance = 2200 μmhos.
Amplification Factor = 17.

I decided to do transconductance next because it is easier. Transconductance, abbreviated Gm is the change in plate current divided by the change in grid voltage with plate voltage held constant. So I must set the plate voltage to a constant value, sweep the grid voltage, and plot the plate current.

To do this V1 must have its value set to 100 volts and later 250 volts.
So, edit the V1 Value to 100.
Edit the .dc directive as follows. ".dc V2 0.5 -0.5 1"
Also edit the line near the bottom that has a star at the beginning to read "* Transconductance".

Here is the formula for transconductance.

Gm= (Ihi - Ilo) / (Vhi - Vlo) = (13.233mA - 10.187mA) / (0.5V - -0.5V) = 3.046mA / 1V = 3.046 mMHOS
= 3046 μmhos. The tube manual value is 3100 μmhos.

Now set the plate voltage to 250 volts and the grid voltage to change from -8 to -9 volts.
I hope by now you know how to do both of these.
I got 2206 μmhos. The tube manual value is 2200 μmhos.

Figure 5.13 Showing Setup for Measuring Transconductance.

The tube manual values are;
Vp = 100 V, Vg = 0, Gm = 3100 μmhos.
Vp = 250 V, Vg =-8.5 V, Gm = 2200 μmhos.

V1 is set to 100 volts and the cursors are set at +0.5 volts and -0.5 volts to give a "change of grid voltage" that is symmetrical about zero. The transconductance IS the slope of the line. When the slope value is converted to micro mhos by moving the decimal point 6 places to the right it turns out to be 3046 µmhos. That's an error of -1.74%.

When V1 Is set to 250 volts and the simulation run again the value of Gm is 2205 μmhos. This was done by setting the cursors at -8.0 and 9.0 grid volts.

Amplification Factor μ.

Plate voltage = 100 Volts,
Grid voltage = 0
Plate current = 11.8 mA.
Plate resistance = 6500 ohms.
Transconductance = 3100 μmhos.
Amplification Factor = 20.

Plate voltage =250 Volts,
Grid voltage = -8.5 Volts,
Plate current = 10.5 mA.
Plate resistance = 7700 ohms.
Transconductance = 2200 μmhos.
Amplification Factor = 17.

The definition of amplification factor is change in plate voltage / change in grid voltage with plate current held constant. That means a current source in the plate circuit rather than a voltage source. Spice doesn't like a current source in the plate of a tube and it generates an error. The cure which has an insignificant effect on the numerical results is to connect a 10 Meg ohm resistor across the current source.

Edit your netlist as follows. Change the V1 line to this.
"I1 0 N001 11.8mA"
Add this line to the netlist.
"R1 N001 0 10Meg"
Change the .dc line to step V2 from -0.5V to 0.5V in a step of 1V.
Run the simulation and read the results.

The value of amplification factor must be calculated from these values. The formula is,

μ = (Vphi - Vplo) / (Vghi - Vglo)

Remember that 0.5 is higher than -0.5. I don't expect you'll have any trouble with 111 and 90.4.

Now change the value of I1 to 10.5mA and,
Change the .dc line to step V2 from -8V to -9V in a step of 1V.
Run the simulation and read the results.
Calculate amplification factor from the formula given above.

The first values come from the tube manual. The values after the word "Simulation" are from that source.

Vp = 100 V, Vg = 0, μ = 20. Simulated, 20.59.
Vp = 250 V, Vg =-8.5 V, μ = 17. Simulated 16.92.

Figure 5.14 Showing Setup for Measuring Amplification Factor.

The popup box has been repositioned to allow both ends of the plate voltage curve to be seen.

The accuracy of these results speaks well for the tube models. The only thing that is less than ideal is the behavior when the grid voltage is zero or positive. In my tube manual the zero volt line has much less upward concavity than in the spice model. In some triodes the Vg = 0 curve is a bit convex rather than being concave as all the other values are. I wonder how hard it would be to model the positive grid performance of tubes.

Example 5.1, Two RLC Band Pass Filter Circuits.

I can't think of any way to do the following in a nonvisual way. It is meant to illustrate how the visually oriented can draw a mistaken conclusion based on graphs that have been deliberately manipulated to cause such wrong conclusions. Although it is likely in months to come I will be corrected but at this time I don't see any way in which the totally blind could be fooled. As explained above I am leaving this material in place for the benefit of any partials who may be viewing this page.

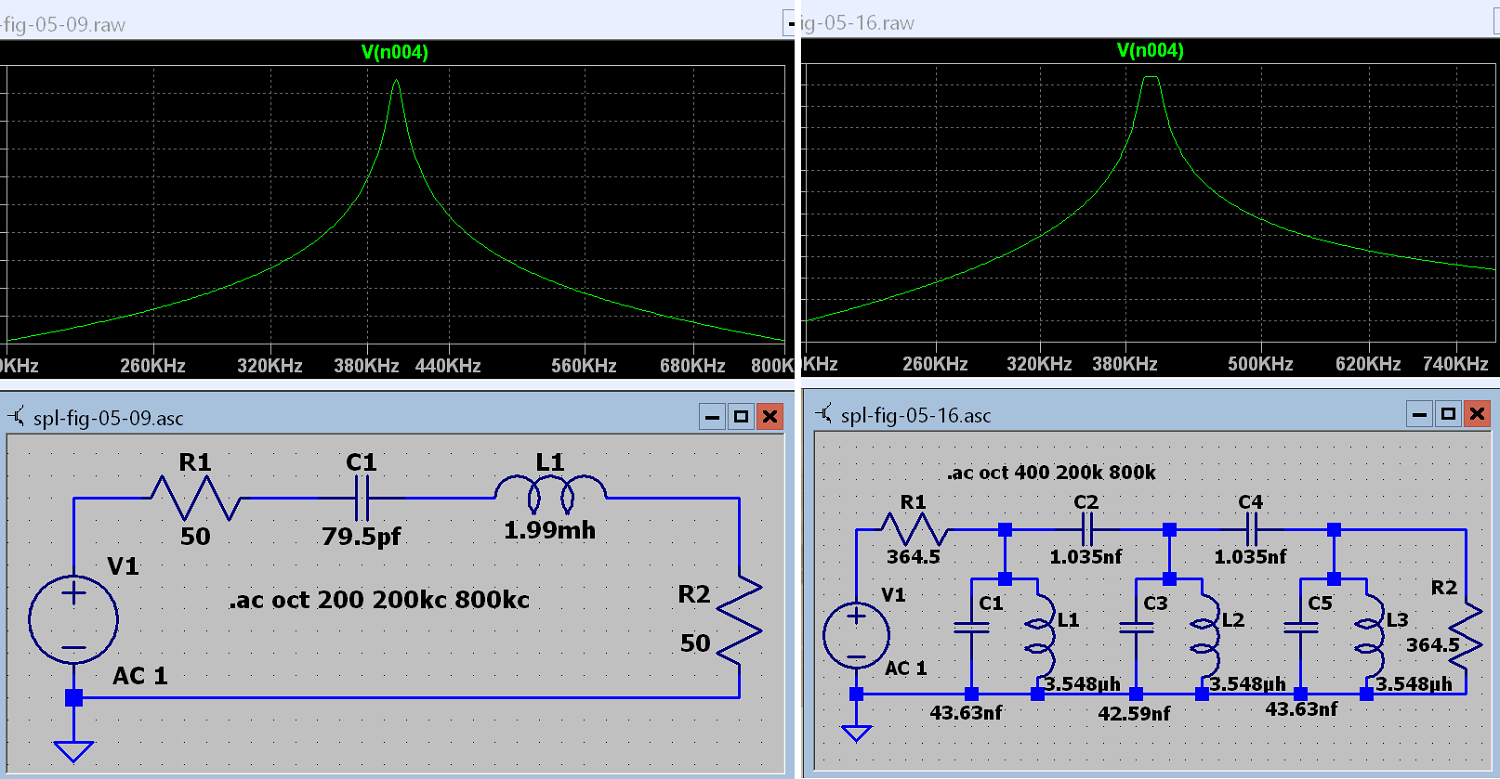
Figure 5.15 Comparing two Different Band Pass Filters.

A professor who is teaching a course in radio receiver design presents figure 5.15 to his students and asks the following question. "Compare and contrast the two filter circuits, point out the advantages and disadvantages of each when used as the intermediate frequency filter in an amplitude modulation radio receiver." The question is printed at the top of a page and the rest of the page is blank. If you were a student in this class how would you answer the question?

This is a trick question. Note that the vertical scales which are attenuation in dB have been cropped out of the picture. The students should answer the question based on the schematic diagrams rather than the frequency graphs. The circuit on the left has only one tuned circuit while the one on the right has 3. The purpose of the IF filter is to pass the wanted signal and attenuate signals on nearby channels. When it comes to receiving the wanted channel and not hearing the adjacent channels, number of tuned circuits is what it's all about. A student who is doing well in the class would know this. One who is not doing so well would likely answer something like this.

The filter on the left is obviously superior to the one on the right. The passband is narrower and has steeper sides. The out of band attenuation is symmetrical and larger than the one on the right.

The answering student made an assumption that both graphs had the same vertical scale. This is not true. Below are the same two graphs but with the scales showing this time and minus the schematic. Not only that, they have been set to be the same. Also cursors are showing on the graphs to provide information about the actual bandwidth of the filter. In receiver design the bandwidth is defined in terms of the -6 dB points rather than the audio standard of -3 dB points. The attenuation from the generator to the output load resistor is 6 dB so the bandwidth limits are taken at -12 dB.

Figure 5.16 Comparing the same two Band Pass Filters but with equal scales this time.

What say you now? The out of band attenuation of the single tuned circuit filter is revealed by the cursers to be -43.5 dB at both 200 and 800 kHz. The stop band is symmetrical but that's the only good thing that can be said about this filter. Although the readout box states "ratio" the frequency at the bottom is the difference not the ratio. This is good because we are given the bandwidth without having to reach for our calculators. It seems as if the folks at LT were a little careless with their labeling. We must admit that the wonderful job they have done in developing this tool means they can be forgiven for a few oversights. And the price is right too.

The point of the above is not to teach band pass filters but to make the point about jumping to conclusions based on incomplete data. LTspice is just another tool. Like any tool if you misuse it, there are likely to be consequences. The good thing is you can't burn your hand or lose a finger by misusing LTspice but you should always remember that it will never replace a breadboard and prototype. Always keep that in mind as you have fun with simulated tubes.

DON'T FORGET TO SAVE THE DRAWING. Save it as Lesson 05.

If you can honestly checkoff each item on the list under the heading "What you will learn in lesson 5", you can go on to lesson 6, assuming I have written it by then.

This page last updated Saturday, March 14, 2020.

Home.