Consider the unit circle given by:

 x² + y² = 1

    Imagine that the real number line is wrapped around this circle, with positive numbers corresponding to a counterclockwise wrapping and negative numbers corresponding to a clockwise wrapping as shown in figures below.

   As the real number wrapping around the unit circle, each real number t corresponds to a point (x,y) on the circle.

Quadrant 

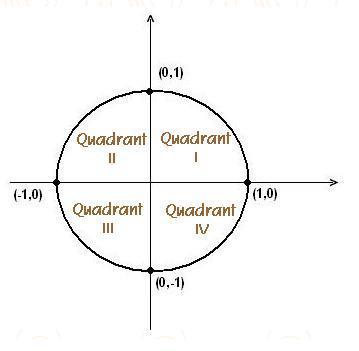
Quadrant I:        0 < q < ¶/2

Quadrant II       ¶/2 < q < ¶

Quadrant III      ¶ < q < 3¶/2

Quadrant IV     3¶/2 < q < 2¶

Practice Problems:

        Determine the quadrant in which the angle lies

          1) a.  ¶/5                 b. 7¶/5

          2) a. - ¶/12              b. -11¶/9

          3) a. 3.5                   b. 2.25