
V(r): Es el campo vectorial de un fluido
F: Superficie
n: Vector normal a F
n.v: Componente de V(r) normal a dF
dq: Infinitesimal del flujo por unidad de superficie y tiempo
![]()
![]()
La cantidad infinitesimal del flujo que atraviesa un dF es la componente normal a dF = n V(r)
![]()
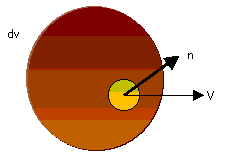
Se encierra con F a un volumen "v" de elemento dv.
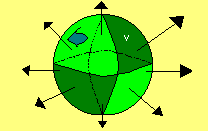
Si la cantidad de fluido que atraviesa la superficie cerrada es diferente de cero, dentro de la superficie debe haber una fuente.
![]()
Se tiene que la Divergencia es:
![]()
La Divergencia es una medida de la productividad de Fuentes por unidad de volumen, y se puede concluir que:
Si la divV = 0, entonces, el campo V no tiene fuentes que lo generen.
LA EXPRESIÓN DE LA DIVERGENCIA
Se tiene un elemento prismático en un sistema de coordenadas
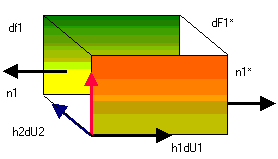
.- La cantidad de fluido que atraviesa la superficie dF1 para U1 constante es dq = dq(U1, U2,U3).
.- La cantidad de fluido que atraviesa dF1* para U1 + dU1 constante es dq(U1+dU1,U2,U3).
dQ1: Es el flujo total en dirección n1
dQ1= dq(U1,U2,U3) – dq(U1+dU1,U2,U3)
con el diferencial se tiene:
![]()
La carga en el volumen disminuye por eso aparece el signo negativo.
![]()
![]()
![]()
en donde dF1 es : dF1 = (h2h3)dU2dU3
![]()
![]()
![]()
El flujo Total del Prisma es
dQ = dQ1+dQ2+dQ3
![]()
![]()
Entonces se tiene la forma general de la divergencia:
![]()
U1 = X ; U2 = Y ; U3 = Z ; h1 = h2 = h3 = 1 ; V1 = Vx ; V2 = Vy ; V3 = Vz
![]()
LA DIVERGENCIA DE UN CAMPO GRADIENTAL
j
: Es una función posición escalar. Por ejemplo el POTENCIALV: grad
j . Esta es una función vectorial
![]()
en donde
D es el operador de Laplace.
La forma general para gradj es:
![]()
![]()
divV(r) = div grad
j
![]()
![]()
![]()
![]()
La forma general del Operador de Laplace es
![]()
En Coordenadas Cartesianas:
h1 = h2 = h3 = 1; U1 = X ; U2 = Y ; U3 = Z.
![]()
EL TEOREMA DE LA DIVERGENCIA DE GAUSS
Como punto de partida se tiene el concepto de la divergencia:
![]()
![]()
![]()
Se toma como ejemplo un volumen cúbico:
Se divide el volumen en segmentos infinitesimales:
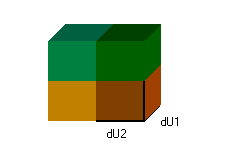
dv= dU1+dU2+dU3+...+dUn
Para mejor observación se separan los segmentos que conforman el volumen:

![]()
En las superficies de contacto interno las normales tienen sentido opuesto, por tanto sus componentes vectoriales dan como resultado CERO.
Solo aparece el flujo a través de la superficie externa del volumen.
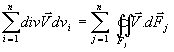
TEOREMA de Gauss: Determinar la productividad de todas las fuentes contenidas en un volumen cerrado, es equivalente a determinar el campo que atraviesa toda la superficie de contorno del volumen.
![]()
EL TEOREMA DE GAUSS MODIFICADO
A: Vector constante en el espacio.
j
: Función escalar
![]()
V =
j A
![]()
![]()
[
PÁGINA PRINCIPAL] [SIGUIENTE][
CONOCIMIENTOS BÁSICOS] [PRINCIPIOS DEL CAMPO ELÉCTRICO ESTACIONARIO][
PRINCIPIOS DEL CAMPO MAGNÉTICO ESTACIONARIO] [LAS ECUACIONES DE MAXWELL][
POTECIAL ELECTRODINÁMICO] [PROPAGACIÓN DE ONDAS]