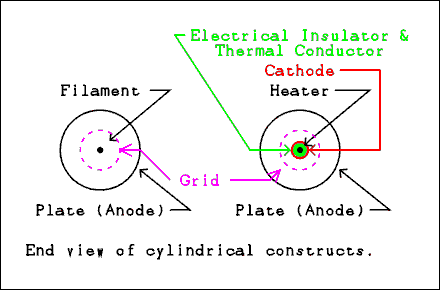
Figure 4A.1 (a) filament type triode
and (b) heater type triode.
For a verbal description click here.
Chapter 4A Triode Vacuum Tubes.
4A.1 The Triode (3 Element) Vacuum Tube.
4A.2 Triode Amplifier Graphical Analysis, Load Line.
4A.3 Triode Amplifier Small Signal Analysis.
4A.4 Resistance Coupled Amplifier Charts.
4A.5 The Miller Effect.
4A.6 Cathode Follower.
4A.7 Grounded Grid Amplifier.
4A.8 Cascode Amplifier.
4A.9 Problems.
4A.10 Answers to Problems.
Chapter 4A.
Triode Vacuum Tubes.
This chapter was not a part of the original textbook. Throughout most of my teaching career I assumed that the vacuum tube was dead. Somehow it kept coming back and saying "the rumors of my death are greatly exaggerated." My department head would not have looked kindly on the inclusion of a chapter on tubes because they were considered by physicists to be obsolete technology and not worthy of being taught in a modern physics department.After retiring I decided to put up a web site devoted to tube technology and see how much attention it would attract. I was amazed by the response. It seems that the venerable old gal just won't roll over and die the way some would like her to do. She won't even play dead. Because this book is linked from both a tube and transistor site I need to put in a good chapter on tube theory and practice. So here it is.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.1 The Triode (3 Element) Vacuum Tube.
The tri part of triode means 3. There are three elements in a triode, the cathode, grid, and plate or anode. The heater doesn't count since it doesn't take part in the operation, it just provides the heat.history.
In the United States Lee De Forest is generally credited with inventing the triode. His claim is under considerable dispute particularly in the United Kingdom. Since I wasn't there I don't know what happened but I have my suspicions. Court records of a case of De Forest versus Armstrong make it clear that De Forest didn't really understand the operation of the tube. That doesn't prove that he didn't invent it, maybe he stumbled onto it by accident. Maybe he ripped off someone else. Even though it all happened barely 100 years ago the mists of history have already settled over the facts and likely we will never know. We have the three element tube even if we aren't quite sure who to thank for it.How it is made.
Photographs of the early Audions show a big spherical bulb with a filament like that in Edison's light bulb. Next to the filament is a grid which looks like hardware cloth (a very course window screen) and a flat plate. Modern triodes are usually cylindrical in construction with the filament or heater/cathode at the center, the grid surrounding it and the plate surrounding all as shown in Figure 4A.1 below.

Figure 4A.1 (a) filament type triode
and (b) heater type triode.
For a verbal description click here.
In these cylindrical tubes the grid takes the form of a helix, like a cork screw or spring. If you happen to have a 6AS7G or 6080WA in your tube collection you can see this construction. The plate instead of being continuous has an opening that runs the length of the cylinder and the shiny grid is clearly visible. There is a 9 pin miniature tube with the same construction but I don't know its number. I saw it once while looking for another tube and I didn't write it down.How it works.
I've made that joke too many times already. Electrons are emitted from the cathode exactly the same as in a diode. They collect in a space charge around the cathode and protect it from heavy positive ions that could do serious damage. In normal operation the grid is made negative with respect to the cathode and never goes positive. (Except in radio transmitters). The grid does not attract electrons and because its wires are very thin, in modern tubes, few electrons run into it by accident. The electric field of the grid repels the negatively charged electrons and limits the number that can pass through to the plate. If the grid is made negative enough no electrons at all can get through. As the grid is made less negative it lets more and more electrons through. Figure 4A.2 below shows this by animation.
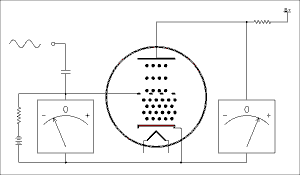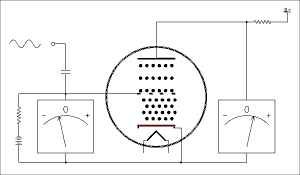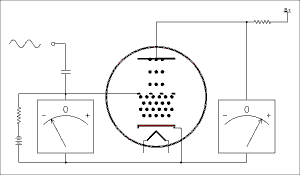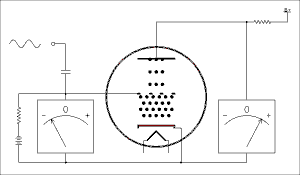
Figure 4A.2 Animation showing the
operation of a triode vacuum tube.
For a verbal description click here.
I know the animation is fascinating but do your best to tear yourself away from it and continue reading. Although the heater connections are not shown it is always assumed they are connected to the proper source of voltage for the heater. As the input signal swings positive the grid becomes less negative. This allows more electrons to get through to the plate which is an increase in plate current. The voltage drop across the plate resistor becomes greater and because the B+ end of the resistor is at a fixed voltage the plate end becomes less positive. You can see right off that as the grid voltage goes up the plate voltage goes down. This is the nature of this type of amplifier circuit. When the input signal swings negative the more negative grid cuts down the number of electrons getting through and the plate current is reduced. This causes the drop across the plate resistor to decrease and the plate voltage gets closer to the B+ voltage, higher. Neither the grid voltage nor the plate voltage gets all the way to zero. If it should, the amount of distortion would be very high.I have found in teaching amplifiers, common emitter as well as common cathode, that students often have trouble grasping the concept of increasing current resulting in decreased voltage. This in spite of demonstrations and laboratory experiments. Let's try using a bungee jumper as an analogy.
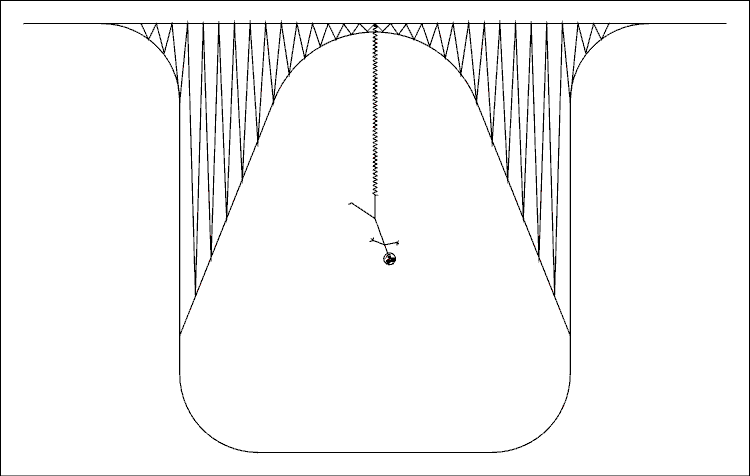
Figure 4A.3 Bungee Jumper Suspended From a Bridge.
For a verbal description click here.
This bungee jumper is in a slightly different situation than all other jumpers. There is an electric current flowing through the bungee cord. The greater the current, the longer the cord gets. As the current increases, the cord gets longer and the jumper gets closer to the ground. As the current decreases, the cord gets shorter and the jumper goes higher. So as the current goes up and down, the hapless jumper goes down and up. If he were to touch the ground or the bridge, his distortion level would be considerably increased.Now remember that the current in a tube is in phase with the grid voltage. As the grid voltage moves up, so does the current. As the above analogy shows the plate voltage is out of phase with the plate current. And that is why a common cathode amplifier inverts the signal.
How it is Used.
Vacuum triodes are used primarily to amplify AC signals. To amplify means to make it bigger. The signals to be amplified are most likely to be in the audio range. Triodes are almost never used to amplify low power radio frequencies such as in a radio receiver. They are often found in high power radio transmitters, but that's another story.An amplifier uses the principle shown in the animation above to increase the voltage of an AC signal. Although the voltmeters in the animation are shown deflecting by the same amount, the voltage in the plate circuit is actually much larger than the voltage in the grid circuit. This is what is meant by amplification.
The tube in the animation is biased by a battery in the grid circuit.*
* In the early days of tubes they were mainly used in radio receivers. Three different batteries were required to power up a radio. These were designated A, B, and C. The A battery lit up the filament, the B battery supplied the plates of the tubes with positive voltage and the C battery supplied the grids of the tubes with negative bias. While A is no longer used as a symbol for the filament or heater supply, (except in portable radios), the terms B and C are still very much with us as will be seen later in this chapter.Figure 4A.4 shows a schematic diagram of a common cathode triode amplifier.
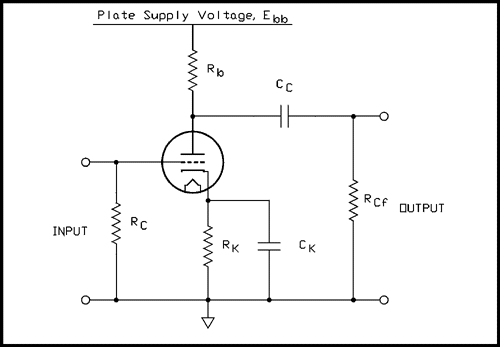
Figure 4A.4 A cathode biased resistance coupled amplifier stage.
For a verbal description click here.
The circuit above is a practical amplifier stage. The B battery is not shown but it is replace by a connection symbol labeled Ebb. The C battery appears to be completely missing but instead of battery bias the tube uses what is often called self bias or cathode bias.Cathode Bias.
Instead of the bias being supplied by an external battery it is developed in the cathode circuit of the tube or to think of it another way by the tube itself.Let's assume that a tube needs the grid to be at -2 volts. That means that the cathode is at zero volts and the grid is at -2 volts. Now suppose we add 2 volts to both values. The grid voltage becomes 0 volts and the cathode voltage becomes +2 volts. The grid is still -2 volts away from the cathode which is required. Think about it. Let your left hand be the grid voltage and your right hand be the cathode voltage. Place your right hand even with the table top at the edge (zero inches) and your left hand 2 inches below your right (-2 inches). Your left hand is below your right hand. Now move both hands up 2 inches. Your left hand is now even with the top of the table (zero inches) and your right hand is 2 inches above it (+2 inches). Your left hand is still 2 inches below your right hand.
To place the cathode of a triode a small number of volts positive you place a resistor in the cathode circuit as shown in Figure 4A.4.
The notation used in this figure is consistent with the resistance coupled amplifier charts found in all tube manuals. Rc is the grid resistor, why not Rg? It's a throw back to the C battery which once supplied the grid bias in early radios. RK and CK are the cathode resistor and capacitor. Yes, they knew that cathode begins with a C but C was already used. Rb is the plate resistor, another throw back to the B battery. CC is the coupling capacitor and Rcf is the grid resistor of the following tube. The plate supply voltage is labeled Ebb. Why Ebb instead of B+? In formal electrical engineering writing the voltage on a tube element is notated as Eb for the plate and Ec for the grid. There is always a resistor between the supply voltage and the element. The supply voltage is distinguished from the voltage on the element by doubling the letter. For example, Ebb, and Ecc just the way it is done in transistors. Hmmm, wasn't it the other way around?
The positive voltage on the cathode is developed by the cathode current flowing through the cathode resistor. The tube, RK, and Rb constitute a simple series circuit. The grid does not take or give any appreciable current.
The capacitor in the cathode circuit is to keep the DC voltage constant. Without this cap the voltage can vary and reduce the gain of the amplifier. This gain reduction is accompanied by a reduction of distortion so in hi-fi circuits the cap is often omitted. More about this later.
Triode Characteristics and Parameters.
The behavior of tubes is described in two ways. One is by a graph of voltages versus currents and the other is by three numerical values called plate resistance, transconductance, and amplification factor. A graph of plate characteristics for a 6SL7 is shown in Figure 4A.5 below.
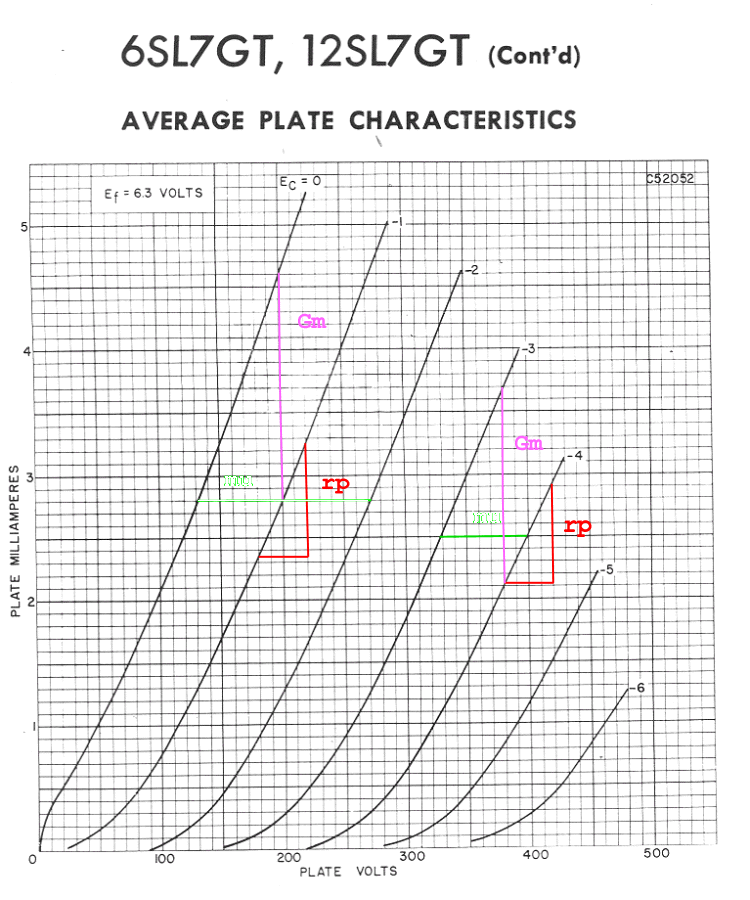
Figure 4A.5 Plate Characteristics of a 6SL7.
For a verbal description click here.
The horizontal axis is the voltage between the plate and cathode, not the voltage between the plate and ground. The vertical axis is plate current, and the number labeling each curve is the voltage between the grid and cathode. We will learn in the next section how to use this graph to design amplifiers and predict the behavior of existing amplifiers.In section 4A.3 we will learn how to use the tube parameters to calculate gain without using the graph. Although we are about to pick parameter values off the graph these parameter values can be looked up in a tube manual. The purpose of picking them from the graph is to illustrate how they are defined.
Plate Resistance.
The plate resistance is NOT the resistor in the plate circuit of a tube. It is a parameter of the tube that is a voltage divided by a current which means its units are ohms. The plate resistance is symbolized by rp. The lower case r indicates that it isn't a real resistor. The plate resistance is defined as,rp = change in Eb / change in Ib, with Ec constant. (4A.1) Where Eb is the voltage between plate and cathode, Ib is the plate current, and Ec is the voltage between grid and cathode. In the graph above you take the change in plate voltage and current along one of the grid voltage lines. It is shown as being taken at two locations. At one place the voltage goes from 180 to 220 volts while the current goes from 2.33 mA to 3.25 mA. This works out to,rp = (220 - 180 v) / (3.25 - 2.33 mA) = 43.5 k ohms. The other point is,rp = (420 - 380 v) / (2.91 - 2.12 mA) = 50.6 k ohms. The tube manual states the parameters at a plate voltage of 200 volts and a current of 2.3 mA. Compare the results from the graph with the tube manual value of 44.0 k ohms. Not bad.Amplification Factor.
The amplification factor is symbolized by the Greek letter μ and is defined as follows.μ = change in Eb / Ec with Ib constant. (4A.2) Where Eb is the voltage between plate and cathode, Ib is the plate current, and Ec is the voltage between grid and cathode. The amplification factor must be taken along a horizontal line which is constant current. The line must start on one grid voltage line and end on another one. The two values around 200 volts and 400 volts are,μ = (131 - 271 v) / (0 - [-2] v) = -70. Although the tube manual never states μ as a negative number, it needs to be one for the calculations that will be performed in section 4A.3.μ = (328 - 400 v) / (-3 - [-4] v) = -72.
Transconductance.
The transconductance is redundant because,Gm = μ / rp (4A.3) Where Gm is the transconductance usually given in micro mhos. Transconductance exists because the calculations on pentode tubes become easier when it is used instead of μ. The definition is,Gm = change in Ib / change in Ec with Eb constant (4A.4) From the curves above the values are,Gm = (4.61 - 2.8 mA) / (0 - [-1]) = 1,810 micro mhos. The tube manual value is 1600 micro mhos. Calculating Gm from equation 4A.3 gives 1,609 and 1,423 micro mhos.Gm = (3.7 - 2.12 mA) / (-3 - [-4]) = 1,580 micro mhos.
Parameter values are highly dependant on the operating point, plate voltage and current. If we had picked off values from lower down on the graph, say 0.5 mA, the parameters would have been quite far from the stated tube manual values. For use in calculations the most accurate parameter values can be obtained by picking them off the graph at the actual operating point.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.2 Triode Amplifier Graphical Analysis, Load Line.
Some find graphical analysis to be too tedious for their taste. However, if curves are available, it is the most accurate method of predicting the DC operating point and AC gain of a resistance coupled amplifier.** The resistance coupled amplifier charts which we will cover in 4A.4 are much easier and just as accurate but they are restricted to one or two values of plate voltage and a few values of resistance. Graphical analysis can give accurate results over a wide range of plate supply voltages and load resistances.The set of curves for the 6SL7 in figure 4A.6 show a complete graphical analysis. Resistance values were taken from the often mentioned resistance coupled amplifier charts to provide a standard of comparison. The data from the RCAC are tabulated along with the results of the graphical analysis at the end of this section.If your screen is set to less than 1280 by 1024 this graph will overflow your screen. Most of the action is in the lower left corner so you shouldn't need to use your scroll bars very much.
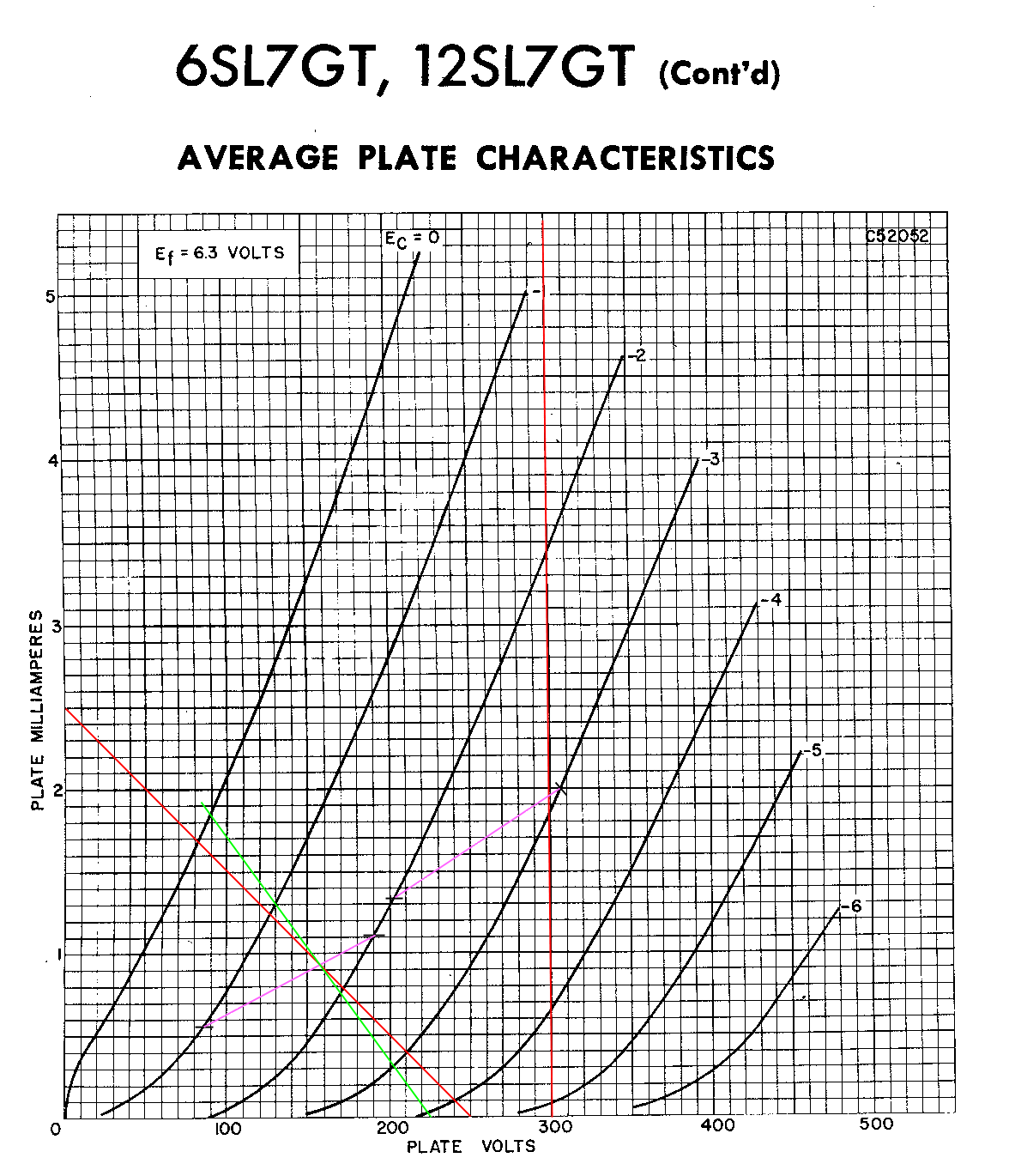
Figure 4A.6 Plate Characteristics with Graphical Solution.
For a verbal description click here.
DC Load Line.
Lower right end of DC load line = Ebb (4A.5)
Upper left end of DC load line = Ebb / Rb (4A.6)
We start with the value of load resistor and plate supply voltage. They are 100 k ohms and 250 volts respectively. The load line runs from zero current and full Ebb* and zero voltage and the current that would flow if the full value of Ebb was applied across the load. I = V / R = 250 / 100 k ohms = 2.5 mA. So we draw a line from 250 volts to 2.5 mA as shown by the red line in the figure.
Ignore the vertical red line and the magenta line that intersects with it. These are used in a later section.
With a 100 k ohm resistor in the plate circuit the tube can operate anywhere along the load line. For example, if we set the plate current to 1.5 mA the plate voltage, across the tube not the resistor, is 105 volts. If we set the plate current to 1 mA the voltage will be 153 volts. If we set the plate current to 0.5 mA the voltage will be 200 volts. If we were to use fixed bias on the tube we could operate it anywhere we wanted to on the load line but never off of it.
Bias Line.
If the tube is self biased, that is if a resistor is placed in the cathode, we would like to know where the tube will operate. We can do that by placing a bias line on the graph. Say we are using a 1.8 k ohm resistor in the cathode. If we placed 1 volt across the 1.8 k ohm resistor the current would be 0.555 mA. We mark this point on the -1 volt grid voltage curve. Now if we placed 2 volts across the 1.8 k ohm resistor the current would be 1.111 mA. We mark this point on the -2 volt grid voltage line and then connect the two points with a magenta line. Where the bias line crosses the load line is where the tube will operate. This is in remarkable agreement with the data from the RCAC. The operating point is often called the quiescent point or for short, the Q-point.AC Load Line.
There is one more line on the graph to be explained. It is the green line which is an AC load line. The signal on the plate of the tube is of no use to us if we can't get it off and do something with it such as send it to the grid of another tube. That next tube will, and must, have a resistor from its grid to ground. A capacitor couples the signal from the plate of our tube to the next one. Assume the resistor in the grid of the next tube is 270 k ohms. The AC load on the tube is not 100 k ohms but the parallel combination of 100 k ohms and 270 k ohms which is 72.97 k ohms. We must place another line on the graph that has a slope of 1/72,970. That can be a little tricky. We start by finding the lower right end of the line.Lower right end of load line = EbQ + IbQ x AC Load (4A.7) Where EbQ is the Q-point plate voltage, IbQ is the Q-point current, and AC Load is the parallel combination of the plate resistor and the following stage's grid resistor. So the lower right end of the AC load line is,L-R AC L-L = 157 v + 0.93 mA x 72.97 k ohms = 225 volts. Start the line at the bottom of the graph at 225 volts and make sure it passes through the point where the load line and bias line intersect. You only need to extend it as far as the zero grid voltage curve.Voltage Gain.
The gain is the change in plate voltage divided by the change in grid voltage along the AC load line. The Q-point is between the -1 and -2 volt grid voltage lines so we might as well use these. At -1 volt the plate voltage is 130 volts. At -2 volts the plate voltage is 170 volts. The gain is (170 - 130) / (-2 - [-1]) = -40.I did not precook this example. I did the numbers and let the chips fall where they may. I too am amazed at how close things came out. The RCAC data comes from laboratory measurements not graphical analysis.
There is no way to reliably evaluate distortion using the graphical method. It is possible to get a feel for it. Between Ec = 0 and -1 the plate voltage changes by 40 volts, between -1 and -2 40 volts, between -2 and -3 31 volts, and between -3 and -4 21 volts. We might be better off to operate the tube at higher current and lower voltage. We must not bias the grid so close to zero that it is driven positive. This will cause the operating point to shift on strong signals and there will be an audible recovery time after the peak.
Description Symbol Value
From
RCACValue
From
Graphic
SolutionPlate
Supply
VoltageEbb 250 Volts -- Plate
Load
ResistorRb 100 k ohms -- Following
Stage Grid
ResistorRcf 270 k ohms -- Cathode
ResistorRk 1.8 k ohm -- Plate
CurrentIb 0.917 mA 0.93 mA Grid Bias
VoltageEc -1.65 volts -1.68 volts Plate
VoltageEb 158.3 volts 157 volts Voltage
GainAV 40.0 40 Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.3 Triode Amplifier Small Signal Analysis.
The small signal calculations are based on the small signal model of a vacuum tube. The triode small signal model is shown in Figure 4A.7 below.
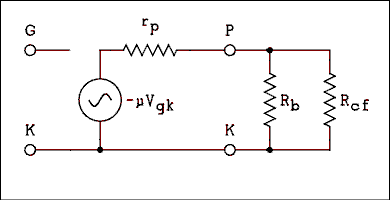
Figure 4A.7 Small Signal Model of a Triode.
For a verbal description click here.
In science and engineering a model is something that represents a real system. It helps people working in the field to visualize the system more easily and make calculations based on the model that will predict the behavior of the real system. The triode tube with its resistors and power supply form a system and can be modeled.As the figure above shows the model consists of a voltage source in series with a resistor. The resistor is symbolized with a lower case r because it is not a real resistor but a part of the model. The Greek letter μ stands for the amplification factor and rp for the plate resistance. These values can be looked up in a tube manual. If we combine the two parallel resistors Rb and Rcf into one and call it Rbc we can write some equations. The current in the circuit is,
I = -μ Vgk / (rp + Rbc) The minus sign comes in because of the phase inversion of the amplifier. If the cathode is grounded then Vgk will be equal to Vin.I = -μ Vin / (rp + Rbc) The output voltage is,Vo = I Rbc Substituting I for I and dividing through by Vin gives,VO / Vin = -μ Rbc / (Rbc + rp) Remembering that the gain AV = VO / Vin we have the voltage gain of a triode amplifier.Av = -μ Rbc / (Rbc + rp) (4A.8) Where Rbc is the parallel combination of Rb and Rcf as follows.Rbc = Rb Rcf / (Rb + Rcf) (4A.9) Example 4A.1.
A 12AX7 has a plate load resistor, Rb, of 220 k ohms and the grid resistor of the following stage, Rcf, is 470 k ohms. Tube manual data on the 12AX7 gives Amplification factor = 100 and plate resistance = 80 k ohms. What is the gain of this 12AX7 amplifierSolution:
First we calculate Rbc.Rbc = Rb Rcf / (Rb + Rcf) = ( 220 k x 470 k ) / ( 220 k + 470 k ) = 150 k ohms.
Now we calculate the gain.
Av = -μ Rbc / ( rp + Rbc ) = -100 x 150 k / ( 80 k + 150 k ) = -65.2
Example 4A.2.
A triode tube is to be used as a single ended low power amplifier. The output transformer has a primary impedance of 5000 ohms. Think of Rb being 5 k ohms and Rcf as not present. Which of the following tubes will give the greatest voltage gain?12AT7, Amplification Factor = 60, Plate Resistance = 10900
12AU7, Amplification Factor = 17, Plate Resistance = 7700
12AV7, Amplification Factor = 41, Plate Resistance = 4800
12AX7, Amplification Factor = 100, Plate Resistance = 80000
Solution:
The gain for each is given by,Av = -μ Rb / ( rp + Rb )
For the 12AT7 it is,
Av = 60 x 5000 / ( 10900 + 5000 ) = -18.9
For the 12AU7 Av = -6.69
For the 12AV7 Av = -20.9
for the 12AX7 Av = -5.88
The 12AV7 comes in first with -20.9 and the 12AT7 is runner-up at -18.9. Notice that the 12AX7 with its impressive amplification factor of 100 comes in last at -5.88. A high amplification factor may not guarantee a high gain amplifier.
Removing the Cathode Bypass Capacitor.
If the cathode bypass capacitor is left out of the circuit, as shown in Figure 4A.8 below, several things about the amplifier will change. The two most important are a reduction of gain and a reduction of distortion. The former is not good by itself but the latter is so good that it is worth the lost gain.
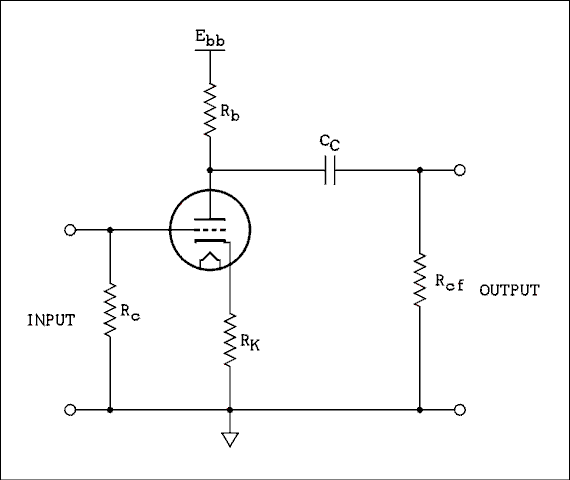
Figure 4A-8 A resistance coupled amplifier
stage with unbypassed cathode resistor.
For a verbal description click here.
Figure 4A-9 Equivalent Circuit of Resistance Coupled
For a verbal description click here.
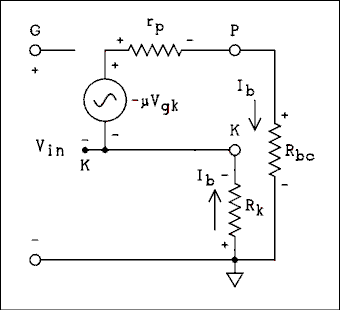
Amplifier Stage with Unbypassed Cathode Resistor.
To derive the equation for the gain of the amplifier without a cathode bypass capacitor we must write loop equations around the loops in figure 4A.9.We write the equation for the input loop up across the Vin generator, not shown, from G to K and back to ground across the cathode resistor.
Vin - Vgk + Ib Rk = 0 (4A.10.1) Then we write the loop equation around the output loop starting at the cathode, up across the generator, around the loop through rp, Rbc, and Rk, back to the cathode.-μ Vgk - Ib rp - Ib Rbc - Ib Rk = 0 (4A.10.2) We want to eliminate Vgk between the two equations.Vgk = Ib Rk + Vin (4A.10.3) Now we factor Ib out of the terms that contain only it.-μ (Ib Rk + Vin) - Ib (rp + Rbc + Rk) = 0 (4A.10.4) Now we multiply μ into the term on the left.-μ Ib Rk - μ Vin - Ib (rp + Rbc + Rk) = 0 (4A.10.5) Now we put the term containing Ib inside the parentheses.-Ib (μ Rk + rp + Rbc + Rk) - μ Vin = 0 (4A.10.6) Now we get Ib on the left side of the equation.-Ib (rp + Rbc + Rk + μ Rk) = μ Vin (4A.10.7) Now we divide by the term that multiplies Ib and carry the minus sign over to the numerator.Ib = -μ Vin / (rp + Rbc + Rk + μ Rk) (4A.10.8) Now we can write Vo = Ib Rbc. We substitute (4A.10.8) into this equation. We also factor Rk out of the two terms in the denominator that contain it.Vo = -μ Vin Rbc / (rp + Rbc + Rk [1 + μ]) (4A.10.9) Now we divide through by Vin and remember that AV = Vo / Vin.Av = Vo / Vin = -μ Rbc / (rp + Rbc + Rk [μ + 1]) (4A.10.10) Where μ is the amplification factor of the tube, rp is the plate resistance Rk is the cathode resistor and Rbc is the parallel combination of Rb and Rcf.Example 4A.3.
A 12AX7 which is without a cathode bypass capacitor has a plate load resistor, Rb, of 220 k ohms, a cathode resistor, Rk, of 3300 ohms, and the grid resistor of the following stage, Rcf, is 470 k ohms. Tube manual data on the 12AX7 gives Amplification factor = 100 and plate resistance = 80 k ohms. What is the gain of this 12AX7 amplifierSolution:
Without a cathode bypass capacitor the gain is given by,Av = μ Rbc / (rp + Rbc + Rk [μ + 1])
Remembering from Example 4A.1 the parallel combination of Rb and Rcf = 150 k ohms and substituting all values gives,
Av = 100 150 k / (80 k + 150 k + 3300 x 101 ) = 26.6
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.4 Resistance Coupled Amplifier Charts.
Probably the easiest way to design a resistance coupled amplifier is to use the resistance coupled amplifier charts found in most tube manuals. If you don't have one you can pick one up on eBay. At any given time there are several for sail and they usually don't cost an arm and a leg. Don't go for one from the 20s, 30s, 40s, or even the 50s. They might leave you a few limbs short. Manuals from the 1960s are usually available and go for $10 to $30. The values found in these charts have been arrived at experimentally rather than by calculation. When it comes to tubes that's often the best way.

Figure 4A.10 Sample page from Sylvania Resistance Coupled Amplifier Chart.
No verbal description is available for this chart.
Yes, I do know how to rotate an image. When I tried reducing it to fit the width of a Windows 98 screen the text became unreadable. So I have kept it readable, big and turned on its side. Just turn your head to the left or download The image to your computer and rotate it yourself.The only part that may need explaining is the zero bias section on the right.
Zero Bias.
An amplifier stage in which the cathode is grounded and there is no external source of bias is called a zero bias amplifier. The bias isn't really zero because the action of the tube will develop a small amount of bias. This is sometimes called contact bias because it is generated by electrons coming in contact with the grid.The grid wires are thin and very few electrons strike them but there are billions of them passing by so even a small percentage is still a very large number. Electrons that strike the grid stick to it and give it a negative charge. If the grid resistor is made very large, say 10 meg ohms, the voltage on the grid will be almost a volt. Now, if the tube has been designed so this voltage is the optimum grid voltage, and some have been, the parts count of the amplifier stage can be reduced by two. A zero biased amplifier is shown in Figure 4A.11 below.
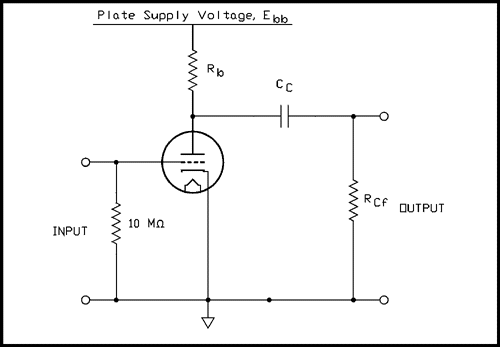
Figure 4A.11 A zero biased resistance coupled amplifier stage.
For a verbal description click here.
This circuit is most commonly used in All American 5 radios but is also seen in guitar amplifiers and hi-fi equipment. If the plate of a previous stage is coupled to a zero biased stage, as is often seen in magnetic phono preamps, a very low leakage capacitor must be used. A very tiny leakage in the capacitor would place a positive voltage on the grid. Even if there is nothing more than the wiper of a pot connected to the grid a DC blocking capacitor must be there to make sure that nothing upsets the bias voltage.Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.5 The Miller Effect.
Anytime any where you have two conductors separated by an insulator you have capacitance. The plate and grid in a triode tube have capacitance between them. Because the tube inverts the signal the capacitance appears to be much bigger than it actually is. Lets explain it with resistors first. In Figure 4A.12a an AC generator is driving a single resistor. In Figure 4A.12b There is another generator in the circuit that always does the opposite of the one on the left but 50 times greater.
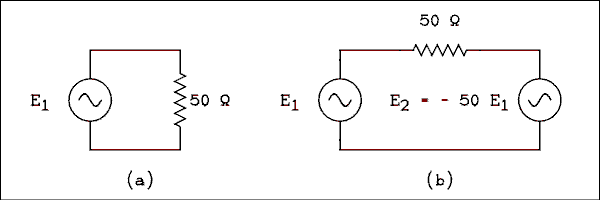
Figure 4A.12 Illustration of the Miller Effect.
For a verbal description click here.
Let us derive a general equation for this situation. Say that E2 = A E1. Summing the voltages around the loop gives.E1 - I R - A E1 = 0 (4A.11.1) Solving this equation for E1 / I will give the effective resistance of the combination of the resistor and the second generator.E1 / I = Reff = R / (1 - A) (4A.11.2) Where A is the factor that relates E2 to E1, R is the resistance of the resistor, and Reff is the effective resistance of R as seen by E1. In this particular case the value of A is -50. If we substitute R = 50 and A = -50 into (4A.11.2) we have,Reff = 50 / 51 = 0.980 ohms. If the generator at E1 is delivering 1 volt, the current through the resistor is I = 1 / 0.980 ohms = 1.02 amps. The 1 volt generator doesn't know about the 50 volt generator on the other end of the 50 ohm resistor. It doesn't know anything, it's just a stupid generator. All it knows is that when it puts out 1 volt it has to deliver 1.02 amps so it thinks it's driving a 0.98 ohm resistor. The second generator has made the resistor look 51 times smaller than it actually is. If a capacitor were to be substituted for the resistor its reactance would look 51 times smaller and since capacitance is inversely proportional to reactance the capacitor will look 51 times bigger.The effective input capacitance of a triode amplifier is given by,
Cinp = Cin + Cgp (1 - Av) (4A.11.3) Where Cinp is the input capacitance of the amplifier, Cin is the tube manual value of input capacitance for the tube and Cgp is the given value of grid to plate capacitance. The value of Gain, A of the amplifier MUST be entered as a negative number. Notice that the factor (1 - A) switched from the denominator to the numerator. XC behaves the same as R but the capacitance is inversely proportional to XC. This causes the factor to be flipped.Example 4A.4
In example 4A.1 we calculated the gain of a 12AX7 amplifier to be 65.2. The tube manual gives the input capacitance of the 12AX7 to be 1.6 pf and grid to plate as 1.7 pf. What is the effective input capacitance of this amplifier.Solution.
Cinp = Cin + Cgp ( Av + 1 )The Miller Effect is some what of a problem even at audio frequencies. The reactance of 114 pf at 10 kc is 140 k ohms. The effective output resistance of the 12AX7 amplifier we have been working with is the parallel combination of the tubes plate resistance, the plate resistor, and the following grid resistor. That works out to 52 k ohms. The upper 3 dB frequency is where Xc = R. If this tube stage were followed by an identical one the cutoff frequency would be f = 1 / (2 π R C ) = 1 / (2 π 52 k 114 pf ) = 26.8 kc. The response would be 1 dB down at approximately half of this frequency. The miller effect can become even more important at radio frequencies.Cinp = 1.6 pf + 66.2 x 1.7 pf = 114 pf.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.6 Cathode Follower.
The cathode follower has a number of properties that make it useful in electronics. It can have an input resistance in excess of 10 Meg ohms and an input capacitance of less than 2 pf contributed by the tube. Wiring capacitance will likely be about 5 pf.The output impedance may be as low as 100 ohms. This makes it very useful when a high resistance source needs to drive a low resistance load.
The cathode follower has a voltage gain of slightly less than unity but it does have current gain which means it qualifies as an amplifier because it increases the power of the input signal. A simple cathode follower is shown in Figure 4A.13.
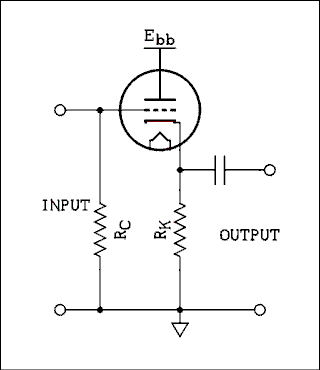
Figure 4A.13 Simple Cathode Follower.
For a verbal description click here.
As the input voltage goes positive the plate current increases which increases the voltage drop across RK. Since the lower end of RK is at ground potential the upper end will get more positive. The cathode can't go up by the exact amount that the grid did. If it did, there would be no net change in voltage between cathode and grid to make the plate current increase. The cathode voltage changes by a little less then the change in grid voltage. It's called a cathode follower because where ever the grid goes the cathode follows along just a little behind.Voltage Gain.
Figure 4A.14 shows the equivalent circuit using the triode model. DC voltages and coupling capacitors are not shown in models so the plate is shown as being grounded.
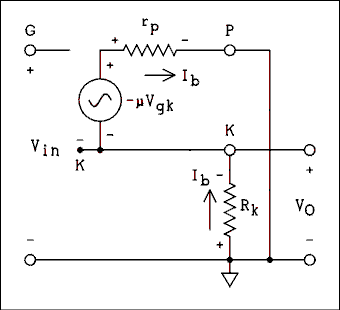
Figure 4A.14 Equivalent Circuit of a Cathode Follower.
For a verbal description click here.
As was done earlier, we will use this model to find the gain. First we write the loop equation around the input loop. As we did above we sum the voltage rises starting at ground, going up through the Vin generator, down from grid to cathode, and then back to ground through Rk.Vin - Vgk + Ib Rk = 0 (4A.12) Then we start at the cathode and sum the voltages around the output loop.-μ Vgk - Ib rp - Ib Rk = 0 (4A.13) Solving (4A.12) for Vgk gives,Vgk = Ib Rk + Vin (4A.14) Substituting (4A.14 into (4A.13) gives,-μ (Ib Rk + Vin) - Ib rp - Ib Rk = 0 (4A.15) Collecting terms and factoring out -Ib gives,-Ib (μ Rk + Rk + rp) - μ Vin = 0 (4A.16) Summing the voltage drops in a counter clockwise direction around the VO and Rk loop gives,Vo + Ib Rk = 0 (4A.17) Solving (4A.17) for -Ib gives,-Ib = Vo / Rk (4A.18) Substituting (4A.18) into (4A.16) gives,(μ Rk + Rk + rp) Vo / (Rk) - μ Vin = 0 (4A.19) Solving (4A.19) for Vo / Vin gives,Vo / Vin = Av = (Rk μ) / (Rk[μ + 1] + rp) (4A.20) If there was a load resistor, RL, connected across the output terminals in Figure 4A.13, The value of Rk to be used in equation 4A.20 would be the parallel combination of RK and RL. Note the case of the K in Rk and RK. The lower case k indicates the AC load while the upper case K is reserved for the DC load.Example 4A.5.
Calculate the gain of a cathode follower with AC loads of, (a) 100 k ohms, (b) 10 k ohms, and (c) 1 k ohm. The tube is a 12AX7 which has a plate resistance of 80 k ohms and an amplification factor of 100.Solution:
We use equation 4A.20.Av = (Rk μ) / (Rk[μ + 1] + rp)
(a). Av = (100 k ohms x 100) / (100 k ohms x 101 + 80 k ohms) = 0.982
(b>. 0.917
(c). 0.552
Example 4A.6.
Which one of the tubes listed below would give the best gain in a cathode follower where RK is 1510 ohms and the load after the capacitor is 200 ohms?6CG7/6SN7, Amplification Factor = 20, Plate Resistance = 7,700 ohms.
12AT7, Amplification Factor = 60, Plate Resistance = 10,900 ohms.
12AU7, Amplification Factor = 17, Plate Resistance = 7,700 ohms.
12AV7, Amplification Factor = 41, Plate Resistance = 4,800 ohms.
12AX7, Amplification Factor = 100, Plate Resistance = 80,000 ohms.
Solution:
Calculating Rk = 1510 x 200 / (1510 + 200) = 176.6 ohms.6CG7/6SN7
Av = 176.6 x 20 / (176.6 x 21 + 7700 = 0.3096
12AT7, Av = 0.4889
12AU7, Av = 0.2760
12AV7, Av = 0.5926
12AX7, Av = 0.1805
The 12AV7 gives the highest gain.
Output impedance.
In order to find the output impedance we replace the cathode resistor with a voltage generator as shown in Figure 4A.15. This could be done in the laboratory if it is done a little differently.
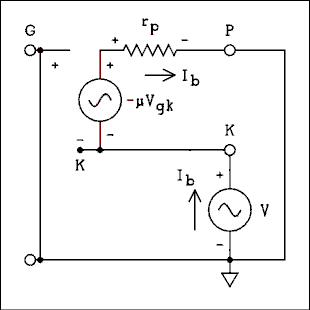
Figure 4A.15 Equivalent Circuit for Output Impedance.
For a verbal description click here.
Note that the input terminals have been shorted. We will now calculate the current Ib which results from the voltage generator V, and divide it into the voltage. Writing the equation around the input loop gives,-Vgk - V = 0 (4A.21) The equation around the output loop is,V - μ Vgk - Ib rp = 0 (4A.22) Solving (4A.21) for Vgk and substituting it into (4A.22) gives.V + μ V - Ib rp = 0 (4A.23) Solving for V / Ib gives,V / Ib = RO = rp / (μ + 1) (4A.25) Example 4A.7.
Which of the 5 tubes listed below has the lowest output impedance?6CG7/6SN7, Amplification Factor = 20, Plate Resistance = 7,700 ohms.
12AT7, Amplification Factor = 60, Plate Resistance = 10,900 ohms.
12AU7, Amplification Factor = 17, Plate Resistance = 7,700 ohms.
12AV7, Amplification Factor = 41, Plate Resistance = 4,800 ohms.
12AX7, Amplification Factor = 100, Plate Resistance = 80,000 ohms.
Solution:
6CG7/6SN7 RO.RO = rp / (&mu + 1) = 7700 / 21 = 366.7 ohms.
12AT7, RO = 178.7 ohms.
12AU7, RO = 427.8 ohms.
12AV7, RO = 114.3 ohms.
12AX7, RO = 792.1 ohms.
Looks like the 12AV7 wins again.
Operating Point.
Plate characteristic curves can be used to determine the Q-point of a cathode follower the same as for a common cathode amplifier. Because the plate connects directly to Ebb the load line goes straight up and down at the value of the voltageFigure 4A.6 is repeated here so you won't have to scroll up to see it. This time look at the other set of lines.

Figure 4A.16 Plate Characteristics with Graphical Solution.
For a verbal description click here.
The plate voltage is 300 volts so the load line is drawn vertically along that line. Let's assume a 1500 ohm resistor from the cathode to ground. 2 volts across 1500 ohms gives a current of 1.333 mA. We mark this point on the -2 volt curve. 3 volts across 1500 ohms gives 2 mA so we mark this point on the -3 line. We connect the points with a magenta line and the tube will operate where the magenta and red lines cross, 1.95 mA.Taking the Cathode Resistor Into Account.
In example 4A.7 we calculated the effective output resistance at the cathode is if there were nothing else connected there. Obviously there is a resistor from the cathode to ground. This resistor is in parallel with the resistance presented by the tube. When calculating the output resistance of a cathode follower the cathode resistor may or may not be significant. Let's do an example where it is.Example 4A.8.
For a 6SL7 calculate the (a) gain and (b) output resistance if a 1500 ohm resistor is used in the cathode. The amplification factor is 70, and the plate resistance is 44000 ohms.Solution:
(a) Av = (Rk μ) / (Rk[μ + 1] + rp)
Av = 1500 x 70 / (1500 x 71 + 44000) = 0.698
(b) RO = rp / (μ + 1) = 44000 / 71 = 620 ohms.
We must now find the parallel combination of Ro with RK.
R = 620 x 1500 / (620 + 1500) = 439 ohms.
Practical Cathode Followers.
The circuit of Figure 4A.13 works but it can be of limited usefulness. The problem is its signal handling capability. The voltage at the cathode may be only one or two volts and the output voltage cannot go negative by anymore than this voltage. The voltage at the cathode can't go negative. This can be gotten around by using one of two circuits.
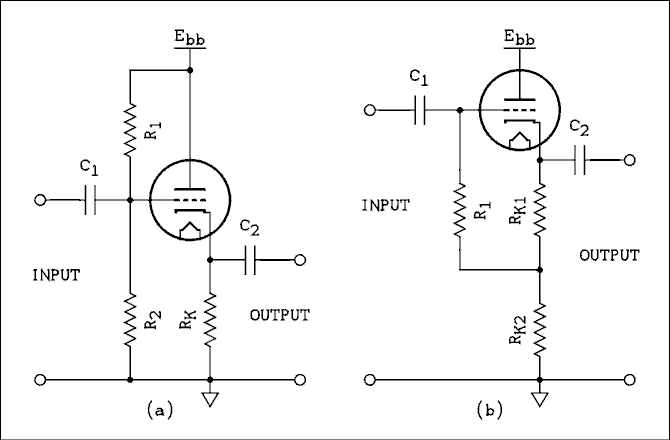
Figure 4A.17 Two Modified Cathode Follower Circuits.
For a verbal description click here.
The circuit in (a) might be preferred by some because it is a bit easier to design. However, it is rarely, if ever, seen. In fact, I have never seen it used in commercially produced equipment.To design it, use the voltage divider equation to select the values of R1 and R2 to set the voltage at the grid. The cathode will be at most 3 volts higher. The value of the cathode resistor may then be calculated based on the desired cathode current. The voltage at the grid may be as high as half of Ebb.
Every tube has a maximum grid resistance stated in the tube manual. The parallel combination of R1 and R2 MUST NOT exceed this value.
Capacitor C1 is an absolute must because there is a DC level at the grid which must not be altered by anything that may be connected to the input.
The circuit of (b) is standard and is known as the modified cathode follower. The two resistors in the cathode bias the grid positive and allow the cathode to be at a much higher potential to permit a larger voltage swing.
When a graphical solution is performed the value of RK1 is used to draw the bias line. The value of RK2 may be what ever is needed to drop the desired cathode voltage up to ½ of Ebb. When doing a graphical solution remember to subtract the voltage drop across RK2 from Ebb and use this number to place the vertical line on the graph. The horizontal axis is labeled "Plate Voltage" but it is actually the voltage between plate and cathode, not between plate and ground.
The major advantage of (b) over (a) is the increased input resistance. R1 has an effective resistance much larger than it actually is because the lower end is connected to a point that is at an AC potential that is in phase with the input signal and just a little smaller. If we assume the voltage at the junction of the three resistors is 0.9 of what is at the input, if the input voltage has a peak value of 1 volt the other end of the resistor has a peak value of 0.9 volts and the voltage drop across the resistor is 0.1 volts. That makes the effective resistance of R1 10 times the actual value of the resistor.
Example 4A.9.
A cathode follower uses a 12AX7 which has an amplification factor of 100 and a plate resistance of 80 k ohms. The resistor values are as follows. Rk1 = 10 k ohms, RK2 = 100 k ohms, and R1 = 470 k ohms. What are, (a) the voltage gain, (b) the output impedance, and (c) the input impedance.Solution:
We must use the sum of RK1 and RK2 for Rk in equation 4A.20.A maximum grid circuit resistance could not be found for this tube but it is usually 2 Meg ohms for small signal triodes. This means that a maximum input impedance of 18.9 Meg ohms could be obtained with this circuit. Using this latter value a corner frequency of 1 cycle per second could be obtained with a capacitor of 0.00844 uf as C1.(a) AV = Rk μ / (Rk[μ + 1] + rp
AV = 110 k x 100 / (110 k x 101 + 80 k) = 0.983
(b) Output resistance of the tube alone is,
Ro = rp / (μ + 1) = 792 ohms.
The true output impedance is this value in parallel with 110 k ohms which is 786 ohms.
(c) We must use (4A.11.2) to calculate the value of Reff, the effective resistance of R1. The question is what value to use for A. We must use the gain between the input and the junction of the three resistors. This is,
A = Av RK2 / (RK1 + RK2) = 0.983 x 100 k / (10 k + 100 k) = 0.894.
The effective resistance of R1 is,
Reff = R1 / (1 - A) = 470 k / (1 - 0.894) = 4.43 Meg ohms.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.7 Grounded Grid Amplifier.
The first impulse would be to say that grounded grid amplifiers are never used in audio circuits. Nothing could be further from the truth. Negative feedback is often injected at the cathode of a stage making it a compound amplifier, both common cathode and grounded grid. Another use is in the long tail pair phase inverter where the signal from the cathode of the left hand tube drives the cathode of the right hand tube which really is in grounded grid mode.The term "grounded" doesn't necessarily mean DC ground although that is the case in many radio frequency power amplifiers. In the next section we will see an RF amplifier in which the grid is at AC ground but a high positive potential. Here is the circuit of a simple resistance coupled grounded grid amplifier.
Many draftsmen will draw the tube with the plate on the right and the cathode on the left. The grid connection point is brought out the bottom and right to ground. I have shown the tube upright because that is the way you are accustomed to seeing it.
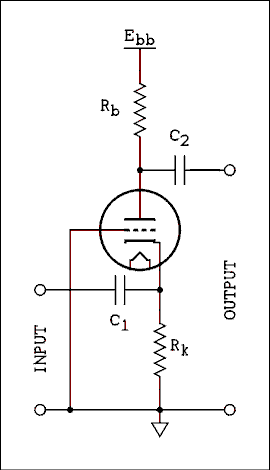
Figure 4A.18 Schematic of Grounded Grid Amplifier.
For a verbal description click here.
Driving the cathode is really no different than driving the grid. The most important difference is the input impedance. Instead of being an open circuit the cathode is a low impedance point as it is in a cathode follower. The other important difference is that the phase of the input signal is NOT inverted. Below is the equivalent circuit.
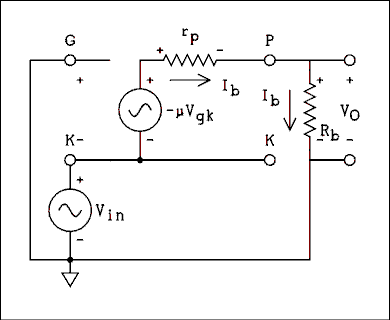
Figure 4A.19 Equivalent Circuit of Grounded Grid Amplifier.
For a verbal description click here.
Notice that the input signal is in series with the tube's voltage source. This is why FCC rules require that when computing the power of a grounded grid amplifier the power of the driver must be added to the power of the amplifier.To derive the gain we write the loop equations as follows.
Vin + Vgk = 0 (4A.26) Solving (4A.26) for Vgk and substituting into (4A.27) gives,Vin - μ Vgk - Ib rp - Ib Rb = 0 (4A.27)
Vin + μ Vin -Ib rp - Ib Rb = 0 (4A.28) Now we write an equation for the output voltage.Ib Rb - Vo = 0 (4A.29) Solving (4A.29) for Ib and substituting into (4A.28) gives,Vin (1 + μ) - (rp + Rb) Vo / Rb = 0 (4A.30) Solving (4A.30) for Vo / Vin gives,Vo / Vin = Av = Rb (μ + 1) / (rp + Rb) (4A.31) The input impedance can be found by returning to equation (4A.28) and solving it for Vin / Ib.Vin / Ib = Rin = (rp + Rb) / (μ + 1) (4A.32) Example 4A.10.
A grounded grid amplifier like that of Figure 4A.18 uses a 12AX7 and has an 1800 ohm resistor in the cathode and a 100 k ohm resistor in the plate. The parameters for the 12AX7 are, μ = 100, and rp = 80 k ohms. What are, (a) the voltage gain, and (b) the input impedance?Solution:
(a) Calculating the voltage gain,The grounded grid amplifier is not used in audio as a stand alone stage. As described above it is hidden in other stages. Where GG amps are found is in RF amplifiers. At radio frequencies the plate to grid capacitance of a triode is enough to cause it to oscillate. The capacitance feeds enough of the plate signal back to the grid to sustain oscillation. Obviously, this is undesirable in an amplifier. The grounded grid acts as an electrostatic shield between the input and output to prevent oscillation. In addition to that the cathode presents a low input impedance and it is not as susceptible to signals being induced as the high impedance grid.Av = Rb (μ + 1) / (rp + Rb)
Av = 100 k x 101 / (80 k + 100 k) = 56.1
(b) Rin = (rp + Rb) / (μ + 1) = 180 k / 101 = 1.78 k ohms.
The input impedance is this resistance, presented by the tube alone, in parallel with the cathode resistor.
Zo = Ro RK / (Ro + RK = 1.78 k x 1.8 k / (1.78 k + 1.8 k) = 895 ohms.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.8 Cascode Amplifier.
The cascode amplifier is never used in audio circuits. I don't know why, maybe no one ever thought of doing it. It gives about as much gain as a pentode with about the same component count. I guess the idea of using two triodes for what would be one stage is just not appealing to audio amplifier designers.The very first stage of a VHF TV receiver or FM receiver must amplify the small signal and add as little noise as possible. The emission and travel of electrons in the tube is a random process and randomness is noise. Pentodes give superior performance at RF because they have inherently higher gain and the screen grid acts as an electrostatic shield between the control grid and plate to keep down oscillation. But those two extra grids give the electrons more opportunities to run into something and produce more random noise. It would be real nice if we could have a tube as quiet as the triode, and with the gain and high input impedance of a pentode.
Enter stage left the cascode amplifier.
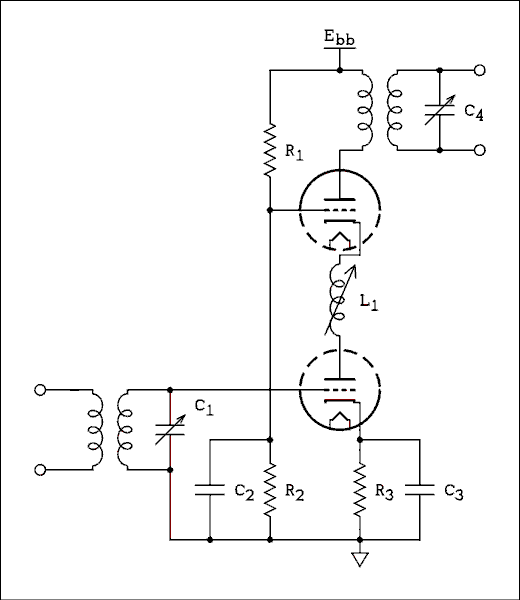
Figure 4A.20 Schematic of Cascode Amplifier.
For a verbal description click here.
This circuit is essentially a common cathode amplifier driving a grounded grid amplifier. The latter provides shielding of the input from the output. There is still some small RF voltage on the plate of the lower tube. There has to be or there wouldn't be any driving signal for the upper tube. The inductor is adjusted to bring the phase of the plate voltage to such a value as to reduce the miller effect in the lower triode to near zero.Cascode amplifiers are constructed using duo triodes such as the 12AT7 which was designed for use in the tuners of early TV sets. The two sections are closely matched and they are in series for DC so the quiescent plate currents will be equal. The resistor network consisting of R1 and R2 is set so the voltages across each triode are equal. This means that μ1 = μ2 and rp1 = rp2.
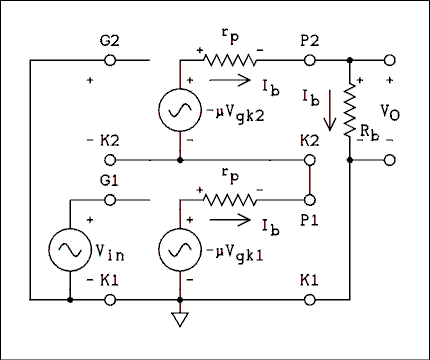
Figure 4A.21 Equivalent Circuit of Cascode Amplifier.
For a verbal description click here.
We don't need to make any distinction between μ and rp for the two triodes. First we write the loop equation in the grid of the lower triode.Vgk1 = Vin (4A.33) Now we start at ground and write the equation around the grid circuit of the upper triode.-Vgk2 + μ Vgk1 + Ib rp = 0 (4A.34) Now we start at ground and write the equation around the main plate circuit loop. Because the two triodes are in series, Ib1 = Ib2 so there is no need to notate them separately.-&mu Vgk1 - Ib rp - μ Vgk2g - Ib rp - Ib Rb = 0 (4A.35) Now we solve equation 4A.34 for Vgk2 and substitute into equation (4A.35)Vgk2 = μ Vgk1 + Ib rp = 0 (4A.36) Substituting equation 4A.33 into equation 4A.37 gives-mu Vgk1 - Ib rp - μ (mu Vgk1 + Ib rp) - Ib rp - Ib Rb = 0 (4A.37)
-μ Vin - Ib rp -μ (μ Vin + Ib rp) - Ib rp - Ib Rb = 0 Now we multiply the parentheses through by μ, collect Ib terms and factor Ib out as a negative quantity.-μ Vin - μ2 Vin -Ib (rp + μ rp + rp + Rb) = 0 Now we factor out -Vin and at the same time factor out rp inside the parentheses.-Vin (μ + μ2) -Ib (rp [μ + 2] + Rb) = 0 Let's factor out μ so we don't have to deal with that μ2 term.-Vin (μ [μ + 1]) -Vo / Rb (rp [μ + 2] + Rb) = 0 (4A.39) To get the output voltage into the equation and eliminate Ib we write equation 4A.40 and substitute it into equation 4A.39.Vo = Ib Rb Now we divide through by -Vin, the parentheses on the right, and multiply by Rb.Ib = Vo / Rb (4A.40)
-Vin (μ [μ + 1]) = Vo / Rb (rp [μ + 2] + Rb) (4A.41)
Vo / -Vin = Rb (μ [μ + 1]) / (rp [μ + 2] + Rb) And finally we multiply through by -1 to obtain,Vo / Vin = Av = -Rb (μ [μ + 1]) / (rp [μ + 2] + Rb) (4A.42) The minus sign is because the amplifier inverts the signal and therefore the gain is a negative number.Example 4A.11.
Calculate the gain of a resistance coupled cascode amplifier using a 12AX7 with a 220 k ohm plate resistor and a 470 k ohm resistor in the grid of the following stage. For the 12AX7, μ = 100, and rp = 80 k ohms.Solution:
Referring back to Example 4A.1 the value of Rbc is 150 k ohms. This is the value to be used for Rb in equation 4A.42.Av = -Rb (μ [μ + 1]) / (rp [μ + 2] + Rb)
Av = -150 k x 100 x 101 / (80 k x 102 + 150 k) = -182
Cascode Versus Pentode in Audio Service.
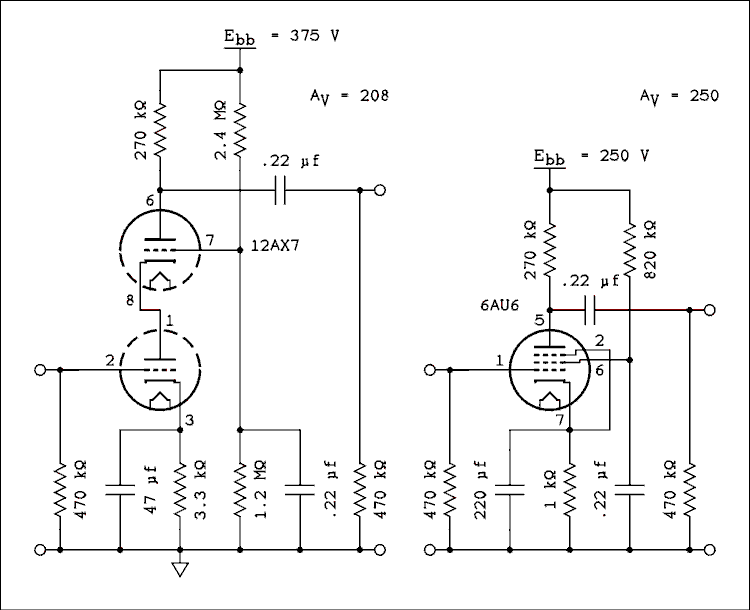
Figure 4A.22 Comparison of Cascode with Pentode Amplifier.
For a verbal description click here.
The figure shows a direct comparison between a cascode amplifier using a 12AX7 and a pentode amplifier using a 6AU6. The parts count is comparable. 1 tube and 3 capacitors for each. The cascode has one more resistor than the pentode but resistors are cheap. True it uses a higher Ebb voltage than the pentode but that could be corrected with a different design.The pentode design was taken intact from the resistance coupled amplifier chart. The capacitors were computed for a 1 cycle per second corner frequency.
The design of the cascode began with the RCAC data. The 12AX7 data for Ebb = 250 volts and the plate and cathode resistors shown gives 128 volts as the quiescent plate voltage. Subtract the approximate 1 volt drop across the cathode resistor and we are real close to half of the Ebb across the tube and half across the plate resistor. With a cascode we make that 1/3 across each tube and 1/3 across the plate resistor and increase the Ebb to 375 volts. Then we calculate the voltage divider in the grid of the top triode to place 1/3 of the supply voltage on the grid. A similar design could be worked out for 250 volts using plate characteristics or a breadboard.
The difference between the gain of the pentode and the cascode only amounts to 1.6 dB. Distortion in the 6AU6 is, by the chart, 1.1% at 25 volts output. The cascode might be a viable solution when high gain and low noise are needed, provided you don't need a lot of output. The measured gain is 200 and here are the distortion figures.
Vo Distortion 25 8.3% 10 2.8% 2 0.56% A cascode is not usable for a high gain high output amplifier. It should have lower noise than a pentode but I don't have time to build a fully shielded version of it to accurately measure the noise output. If one is working close to the noise floor obviously one is not going to be operating at a high level of output so in this application distortion should not be an issue. Noise shouldn't be an issue until the input voltage gets under 1 millivolt. At that level the output voltage would be 200 millivolts and the distortion would likely be unmeasurable.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.9 Problems.
- Use the plate characteristics for the 6SL7 and (a) place a load line on the graph for a plate supply voltage of 400 volts and a resistor of 220 k ohms. (b) Place bias lines on the graph to determine the standard value cathode resistor to give a plate voltage as close as possible to 265 volts. (c) Place an AC load line on the graph for a following stage grid resistor of 470 k ohms. (d) Determine the gain from the AC load line. Note. You will need to print out the plate characteristics to have something to draw on. The best one to print may be Figure 4A.5 as what is drawn on it is all above 2 mA and will be out of your way.
- A 12AU7 has a 100 k ohm resistor as a plate load. The following stage grid resistor is 470 k ohms. For a 12AU7 the amplification factor is 17 and plate resistance is 7700 ohms. What is the voltage gain of this stage?
- A 6SN7 has a plate load of 47 k ohms and an unbypassed cathode resistor of 1 k ohm. There is no following stage grid resistor as this is in a Williamson amplifier phase inverter. The amplification factor is 20 and plate resistance is 7700 ohms. What is the voltage gain of this amplifier?
- It is desired to have a 12AX7 amplifier with a gain as close to 10 as possible. The load resistance is 39 k ohms. Select a cathode resistor to give this gain. The parameters for the 12AX7 are, μ = 100, and rp = 80,000 ohms.
- Design a 6SL7 amplifier from the sample page of a resistance coupled amplifier chart reproduced above. The only requirements are that Rcf must be 470 k ohms, the gain must be between 52 and 53, and the distortion must be less than 0.6%. In your answer state the values of, Ebb, Rb, Rk, (give 0 if zero bias is selected), Esig, Gain, and % Distortion.
- A 12AT6 has a gain of 50. The plate to grid capacitance is 2.0 pf and the input capacitance is 2.2 pf. What is the total input capacitance of the amplifier?
- A 6S4 is a 9 pin triode with a plate dissipation of 7.5 watts which is quite a lot for a small triode. Its amplification factor is 16 and its plate resistance is 3600 ohms. If this triode is used in a cathode follower where the total resistance in the cathode is 2500 ohms, what is (a) the voltage gain, and (b) the output impedance, including the cathode resistor?
- A 6C4 is used as a grounded grid amplifier. The plate resistor is 47 k ohms, the cathode resistor is 1 k ohm, and the following stage grid resistor is 220 k ohms. The tube parameters are μ = 17, and rp = 7,700 ohms. What are (a) the voltage gain, and (b) the input impedance including the cathode resistor.
- A 6SL7 is to be used in a cascode amplifier. The plate resistor is 220 k ohms and the following stage grid resistor is 470 k ohms. What is the gain? Tube parameters are, μ = 70, rp = 44,000 ohms.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.
4A.10 Answers to problems.
- (a) The red line on the graph is the correct load line.
(b) There are two approaches to this problem. One is the estimation method and the other is the limits method. The estimation method goes this way. 265 volts is approximately half way between the -3 and -4 curves. So lets try -3.5 volts and see what happens. The current corresponding to 265 volts is about 0.62 mA. The trial Rk is then,
Rk = 3.5 v / 0.62 ma = 5,645 ohms.
The closest standard value is 5.6 k ohms. Then we check this with a bias line for 5.6 k ohms.
3 / 5.6 k = 0.536 mA
4 / 5.6 k = 0.715 mAWe mark these values on the -3 and -4 grid voltage lines and connect them with a line. Where the bias line and the DC load line cross is the Q-point of the tube. It is always a good idea to check the adjacent values of 4.7 k and 6.8 k.
The limits method goes this way. The desired operating point is between -3 and -4 grid voltage. So we check the cathode resistor where the load line crosses these grid voltage lines.
Rk-min = 3 v / 0.74 mA = 4054 ohms, and
Rk-max = 4 v / 0.51 mA = 7843 ohms.There are 3 10% standard values between these limits. They are, 4.7 k, 5.6 k, and 6.8 k ohms. It is always a good idea to try all three just to be sure. The correct resistor is 5.6 k ohms.
(c) As has been worked in an example, the parallel combination of 220 k ohms and 470 k ohms is 150 k ohms. The current where the DC load line crosses the bias line for 5.6 k ohms is 0.63 mA.
Lower right end of AC load line = EbQn + IbQ x AC load.
Lower right end of AC load line = 264 v + 0.63 mA x 150 k ohms = 358 Volts.Anchor the lower right end at 358 volts and rotate the line until it passes through the point where the DC load line and bias lines cross. Stretch it as far as you can and draw the line. Note. I did these lines on a computer screen. I had to have the image zoomed in pretty far to read the graph. The length of the AC load line was limited by the zoomed area of the graph.
(d) The gain along the AC load line for grid voltages from -3 to -4 volts is 47.
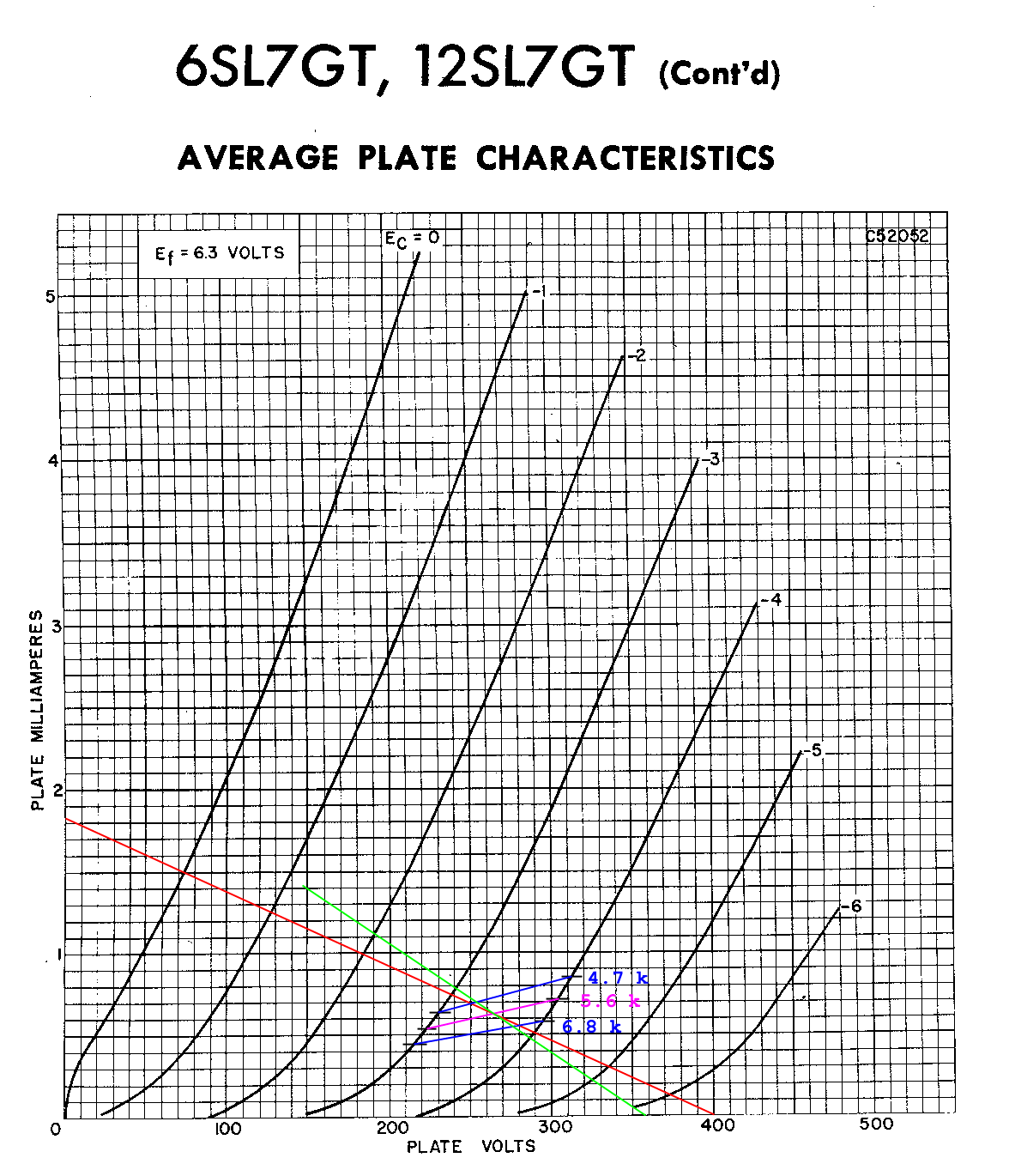
Figure 4A.23 Graphical solution to problem 1.
For a verbal description click here.
- -15.5.
- -12.4.
- 2.7 k ohms.
- There are two possible answers.
Self bias. Ebb = 250 V, Rb = 470 k ohms, Rk = 4.7 k ohms, Esig = 0.1 v, Gain = 52.5, and %Dist = 0.5.
Zero bias. Ebb = 250 V, Rb = 470 k ohms, Rk = 0, Esig = 0.1 v, Gain = 52.5, and %Dist = 0.4.
- 104.2 pf
- (a) 0.868, (b) 195 ohms.
- (a) 15.0, (b) 721 ohms.
- 262.
Back to Fun with Transistors.
Back to Fun with Tubes."
Back to Table of Contents.
Back to top.