How to Pathfind: the Approach in Theory
By William R.C. Smith

The term "pathfinding" refers to the process by which a path is found through an area. The human brain performs pathfinding tasks almost constantly. In order to allow a computer to perform a pathfinding operation, the method my which a path is found must be reduced to a few simple rules. It may seem hard to believe that complicated actions such as finding a path through a maze can be reduced to a computerized step-by-step process. This process is explained below, showing exactly how a path can be found using only these rules.

First we must present the computer with a maze:

This is not really a maze yet, but it gives us an area to work with, complete with a startpoint and endpoint.

Now we can add some walls to make the maze more interesting:

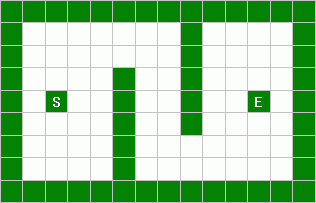
With these walls in place, the best path is clearly no longer a straight line between the start and endpoints. We can be sure now that the computer must do some work to find the best path of squares (also referred to as "nodes") from the start to the end.

Next, we find the distances of the nodes from the startpoint. The startpoint's distance from itself is of course zero. In this figure, all the nodes around the startpoint have been highlighted in red:

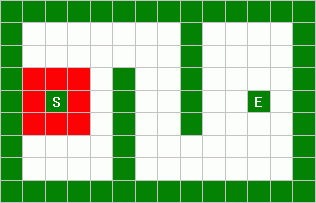
These nodes are one unit away from the startpoint. Therefore we can label them all with a "1" as shown:


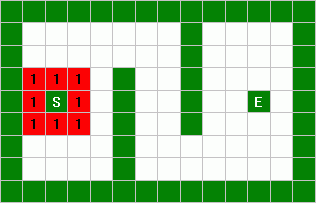
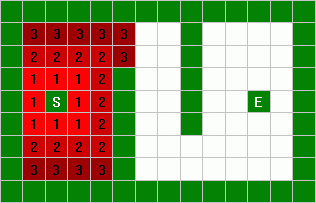
Then we find all nodes that touch, or surround a "1" node, and label them "2", because they are 2 units away from the startpoint.

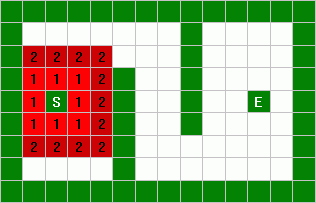
This process is repeated with 3's and 4's:
 

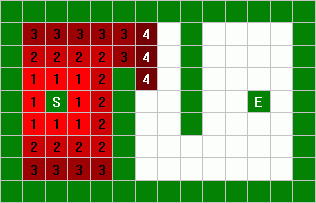
The nodes are labeled with their distance from the startpoint until the endpoint is reached:

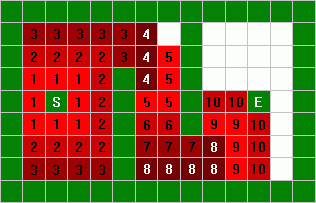
As you can see in this diagram, the endpoint is 10 units away from the startpoint. That is, the best path to the endpoint will be 10 units long.

Now the computer has the 'lay of the land' of the maze, and can find the best path. To do this, the computer starts at the endpoint, and works its way back. The computer looks all around the endpoint (with a distance of 10 units) for a node with a lower value. It finds a node to the lower left with a value of 9, which is less than 10, so that node must be the second to last node in the path.

The computer now looks at all the nodes surrounding the current "9" node, looking for a node with a lower value. It finds a node to the lower left with a value of 8, so that is the next node in the backwards path.

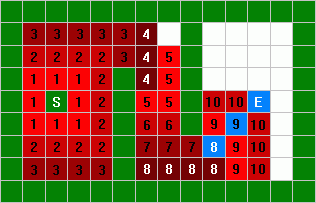
If this pattern is continued, the computer can trace a path from the endpoint all the way back to the startpoint:

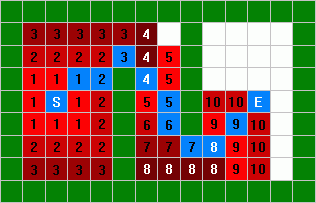
Only the blue nodes matter, because they make up the final path. All the red unused nodes can be forgotten:

All that is left is the best path between the startpoint and the endpoint: A successful pathfind!

This set of concrete rules can be applied to much larger and more complicated mazes. The only restriction to the speed of the pathfind is the size of the maze and the amount of processing power the computer has available to it.

This path was computed through this maze using the same instructions described above: