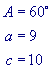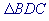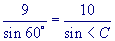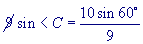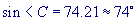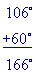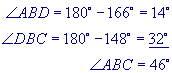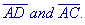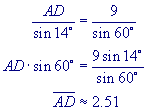First, you must label your triangle correctly! Each angle gets a letter (A, B, or C). To label the sides of a triangle, label it the lower case letter of the opposite angle (a, b, or c). Now you are ready to take these rules into ACTION!
What is the Ambiguous Case anyways?
Definition: When the sine rule results in more than one solution for given data.
With the given data use the Sine Rule to solve for all parts of the first triangle, this should be pretty easy because we've done this before.
When you are given 2 sides and an angle opposite one of the sides, you have what is called the ambiguous case. Also, you will need to find the height in order to determine if it qualifies for the special ambiguous case. The adjacent side of the angle must be larger then the opposite side of the angle, while the height should be greater then the adjacent side and less then the opposite side.
After solving for the first triangle, you will need to swing the opposite side over to form a new triangle. The two sides and the angle will be the same, but you must find the new information! To find your new angles use sine or cosine. To find angle "C," you must take the original value you find from your first triangle and subrtact it from 180.
EXAMPLE
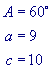
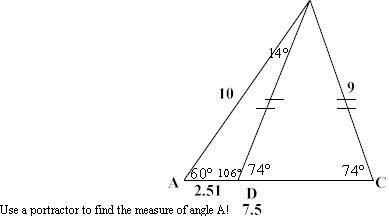
*Note: on the picture it says use a protractor, however ignore this!
Given two sides and an angle opposite one of the sides. We have the ambiguous case. Always find the right-most angle first!
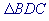
will always be isosceles. ALWAYS!
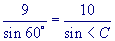
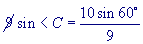
This is the point where you will know if you have NO TRIANGLE. Sine canít be greater than 1!
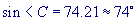
Inverse Sine in the TI-83:
This is how you put the values into the TI-83. Notice you only need to place a parenthesis after the 60.
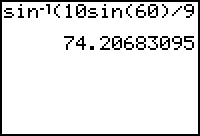

is the supplement of 74 degrees

is 180-74 = 106 degrees
This is where you determine whether you have one triangle or two triangles!
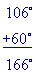
The solutions are
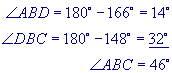
We need
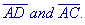
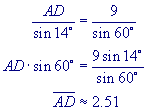

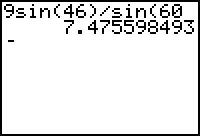
Phew! That was the most difficult lesson ever, but we did and we were so excited when we had finished!