A function is a relation in which no two ordered pairs have the same first element (or every X relates to exactly 1 Y).
To determine if a relation is a function, just follow three easy steps.
- Sketch the graph of the relation
- Visually check to see the number of times a vertical line would cut the graph.
- If the vertical line cuts at one place over the entire graph, then the relation is a function. However, if there is any place where the vertical line would cut at 2 or more places for one X value, then it is not a function.
example: (0,0), (8,9), (5,5), (4,2)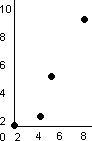
The relation is a function.
The equation for a function is often written as f(x)=equation. F(x) is read as "f of x".
 Back to Relations
Back to Relations
*My apologies for the way <(or equal to) is written. I have been unable to locate the proper symbol (the < with a bar underneath), and the portion "or equal to" is an important part of the problem. Again, my apologies.
This information is taken from the chapter Functions 1 in the IB Mathematical Studies textbook.