# First law of thermodynamics

# First law for a cycle:

Both heat transfer and work transfer may cause the same effect on a system. They both are different forms of energy in transit. Energy that enters a system as heat may leave as work or vice versa.

Consider a closed system ( ) undergoing a cycle between two states 1 and 2.

Let it be brought to state 2 by adding some work to it by rotating the paddle wheel, and returned to state 1 again by transferring heat to the surrounding. It has been found that the amount of this work transferred is always proportional to heat transferred. If the cycle involves many heat and work quantities, same result will be found. So,

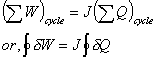
Where, J is called Joule’s equivalent.

When heat and work both are measured in same unit, value of J will be 1.

This is the first law of thermodynamics for a closed system undergoing a cycle. It is a general law of nature since no violation of it has ever been demonstrated.

# First law for a closed system undergoing a change of state.

Consider a system undergoing a cycle, in which it changes from state 1 to state 2 through a process A and returns from state 2 to state 1 through process B.

Now for a cycle, we have

For a cycle made up of two process A and B,

Now consider another cycle using process C and B, then similarly,       

Now subtracting the second from the first equation, we get

On rearranging,

Since, A and C represents arbitrary process between states 1 and 2, the quantity  is same for all processes between states 1 and 2. Therefore,  depends upon only initial and final states, and not on the path followed, so it is a point function and differential of the property of the mass. This property is the Energy of the mass, E.

On integration we get,

₁Q₂ = E₂-E₁ + ₁W₂.

This is the general expression of first law for a process.

The property E represents all the energy contained by the system at given state. If we separate the bulk kinetic energy and potential energy for the property E, remaining all the energy is called the internal energy U,

So, E = U + KE + PE

In differential form,

dE = dU + d (KE) + d(PE)

So, first law for change of state may be written as

dQ = dU + d(KE) + d(PE) + dW

# Internal Energy a property

U is an extensive property and so is KE and PE. Whereas, KE and PE are the stored macroscopic energy, U is the microscopic energy composed of translational, rotational, vibrational, chemical, electronic, nuclear, etc. energy possessed by the molecules of a substance.

  # Internal energy for Ideal Gas:

Joules’ experiment:

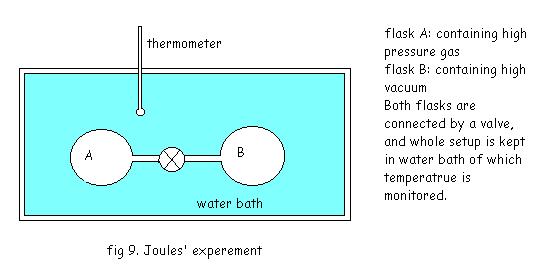
In the setup in the fig. The valve is opened after thermal equilibrium is attained, and the gas in the flask expands against the vacuum in flask B finally filling the both flasks. No, change in the temperature of the bath was detected during or after the process, hence there was no heat transfer in the process, also any work transfer.

So, from first law it can be concluded that the change in internal energy is zero.

Since there was change in pressure and volume of the system, internal energy is not the function of these properties.

The relation between the internal energy U and the temperature can be established by a property called the constant-volume specific heat.

Specific heat is the amount of heat required per unit mass to raise the temperature by one degree. Neglecting change in KE and PE and assuming a simple compressible substance and Quasi-equilibrium process, first law can be given as:

For constant volume, the work (PdV) is zero. So, the specific heat is,

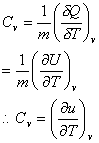
Since, internal energy of an ideal gas is not a function of volume, for ideal gas

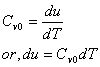                                                Where, C_v0 is the specific heat for ideal gas.

  # Enthalpy

Consider a control mass undergoing a Quasi-static constant- pressure process. Neglecting change in KE and PE, we have,

For a constant pressure process

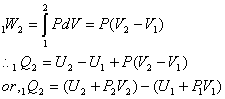
For, this very restricted case, heat transfer is given by change in the quantity U+PV between initial and final states. Since, this combination is also a property and is defined as,

H = U + PV

For, per unit mass,

h = u + Pv

so, for constant pressure process, heat transfer is equal to change in enthalpy. This is by no means a general result. The significance and use of enthalpy is not restricted to the special process just described. In cases, where the combination u + Pv appear, will be represented by enthalpy.

  # Enthalpy for ideal gas:

From definition of enthalpy and the equation of state for ideal gas, we can write

                        h = u + Pv

            or,        h = u + RT

Since, R is a constant and u is a function of temperature only, we have,

              h = f(T)

The relation between enthalpy and temperature can be established by the definition of Constant Pressure specific heat,

For constant pressure process, specific heat,

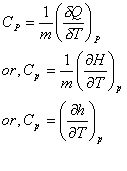
Since enthalpy of ideal gas is not a function of pressure, we can write

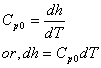                                                                                   Where, C_po is the specific heat for ideal gas.

# First law analysis for a control volume

  A control volume is a volume in space in which one has interest for a particular study or analysis.

Mass, heat and work can cross the control surface and the mass and its properties can change with time in the control volume.

  # Conservation of mass in control volume

The rate of change of mass inside a control volume can be different from zero if we add or take a flow of mass out as

                        Rate of change = +in – out

For several possible flows,

This equation is termed as continuity equation.

  # First law of thermodynamics for control volume

 For control mass, we have the first law as,

as rate equation, we have,

Consider a control volume that involves rate of heat transfer, rates of work transfer and mass flows. Since we cannot create or destroy energy, so any rate of change of energy must be caused by rates of energy in or out of the control volume.

Since heat and work transfer are already included we need explanation about the energy associated with the mass flow rates.

The fluid flowing across the control surface (which envelops the control volume) enters or leaves with an amount of energy per unit mass as,

 Relating to the state and position of the fluid.

Whenever a fluid mass enters a control volume at state i, or exits at state e, there is a boundary movement work associated with that process. Fluid mass enters the control volume as it is pushed by the surrounding against the local pressure with a velocity, giving the control volume a rate of work in the process.

So, the flow work,

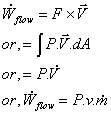
So, the flow work per unit mass is Pv and total ener4gy associated with the flow of mass is,

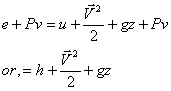
So, first law of thermodynamics for control volume becomes,

For, general control volume we may have several (n) entering or (m) leaving mass flow rates so, for that case, the final form or the first law becomes,

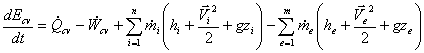
# Steady state steady flow process

Here we establish the first law for control volume for the long-term steady operation of devices like turbines, compressors, nozzles, boilers and condensers.

  SSSF Assumptions

1.        The control volume doesn’t move relative to the co-ordinate frame. (No work associated with the acceleration of the control volume.)

2.       The state of mass at each point in the control volume doesn’t vary with time. (This implies,

3.       The mass flux and its state remain constant with time at the inlets and outlets.

4.       The rate of heat and work transfer across the system boundary remains constant.

So, according to the assumptions the first law of SSSF devices will be,

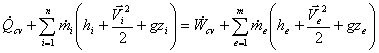
For models having only one inlet and outlet, the continuity equation becomes,

And the first law will be,

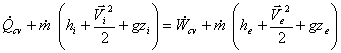
or,       

First law applied to SSSF devices:

1.       Heat Exchanger  
 It is a Device in which heat from one flowing fluid is transferred to another flowing fluid inside a control volume.

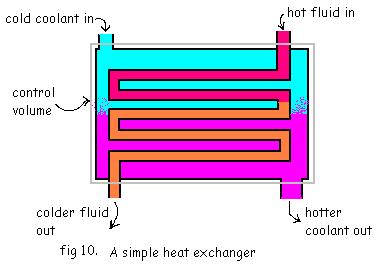
In the ideal heat exchanger

1.        The fluids flowing will have very low pressure drop

2.       There is no means of doing any shaft, electrical etc work through the control volume.

3.       Change in K.E. and P.E. of the fluids is very small.

4.       No heat transfer to or from the surrounding.

 So, for the heat exchanger the continuity equation will be,

And the energy equation will be,

2. Nozzle:  
It is a device to generate a high velocity fluid stream at the expense of its pressure.

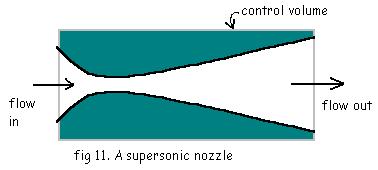
In an ideal nozzle,

1.        The fluid pressure will be dropped and velocity increases significantly.

2.       Neither Work nor Heat crosses the system boundary.

3.       No change in P.E. of the fluid takes place.

4.       K.E. at the inlet is usually small and can be neglected.

So, the continuity equation will be,

And the energy equation will be,

3. Diffuser:  
It is a device constructed to decelerate a high velocity fluid in a manner that results in a increase in pressure of the fluid (opposite to Nozzle). So, its continuity equation and the energy equation will be same as of the Nozzle.

4. Throttle  
It is a device in which a fluid flowing in a line suddenly encounters a restriction in the flow passage (may be plate with a hole, capillary tube).

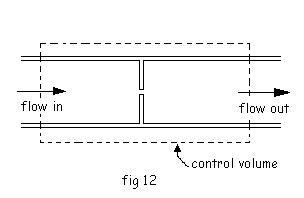
In an ideal throttling device,

1.        Abrupt pressure drop in the fluid occurs

2.       Some increase in velocity will be there but can be neglected because of its very low value.

3.       No work, no change in P.E. no heat transfer to or from the surrounding.

So, the first law reduces to

            h_i= h_e

So, throttling is a constant enthalpy process.

5. Turbine  
It is a rotary SSSF Machine whose purpose is the production of shaft work in expense of pressure of the working fluid.

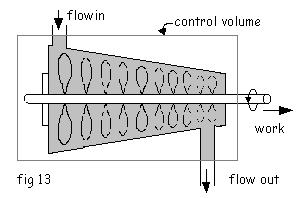
In an ideal turbine

1.        Change in P.E. and K.E. of the flow are negligible.

2.       Heat rejection form the turbine is negligibly small and is undesirable

3.       The turbine process is assumed to be adiabatic

Hence, the first law reduces to

6.  Compressor/ Pump  
It can be a reciprocating or a rotary device whose purpose it to increase the pressure of the fluid by putting in some shaft work through external means. Devices fulfilling this purpose for liquid are termed Pumps and those for gases are termed Compressors. Theoretically, these devices work exactly in opposite to that of turbine. So,

1.        Change in P.E. and K.E. of the flow are negligible.

2.       Heat rejection form the turbine is negligibly small and is undesirable

3.       The turbine process is assumed to be adiabatic

Hence, the first law reduces to

7. Boiler  
It is a device whose purpose it to increase the pressure of a fluid by putting heat through some external means.

In an ideal boiler

1.        Change in K.E. and P.E. of the flow are negligible.

2.       There will be no work interaction with the surrounding.

Hence, the first law for an ideal boiler will be,

# Uniform State Uniform Flow Process

This USUF processes occurs in the devices in which there is provision for change of state of mass of the working fluid. An ideal bottle filling process is an example of USUF process.

Assumptions

1.        The control volume remains constant relative to the co-ordinate frame.

2.       The state of the mass within the control volume may change with time, but at any instant of time the state is uniform throughout the entire control volume.

3.       The state of the mass crossing each of the areas of flow on the control surface is constant with time although the mass flow rates may be time varying.

  The overall USUF process occurs within a span of time t.

Continuity equation at any instant of time is;

Now integrating over time t, we get,

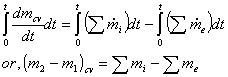
This is the continuity equation for USUF process.

Similarly,

We have Energy Equation at any instant of time;

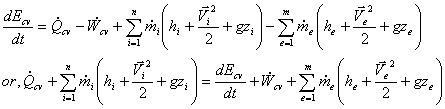
Since, in USUF process, state within the control volume is uniform at any instant of time, we can write,

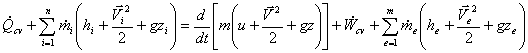
Now integrating over time t, we get

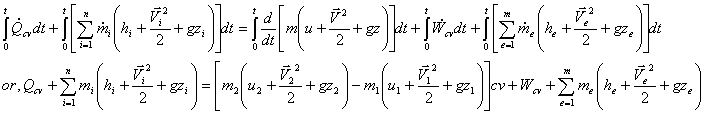
This is the first law of Uniform State Uniform Flow process for period of time t.