algebraic formulas Note: Firefox browser does not display Greek-letter symbols properly. Internet Explorer does.
The most important math skill is the ability to manipulate
and solve
algebraic
formulas. Note that there is a difference between finding a general
solution and evaluating or finding a specific solution.
Finding a general solution to an algebraic expression.
Ohm's law can serve as an example: V = IR[where V is voltage, I is current and R is the restance in an electrical circuit.]
In the listed form, Ohm's law is said to be "solved for V"
because
V
stands alone on one side of the equal sign.
We can solve this equation for I if we divide both sides fo the equation by R; this yields I = V/R,
or we can divide the original form by I to "solve for
R",
R
= V/I.
A second example is the pendulum equation, T = 2p\/( l / g ) , where T is the period of time for one complete swing of the pendulum, l is the length of the pendulum, and g is the acceleeration due to gravity, g = 9.81 m/s2 near the surface of Earth.
Let's say that we want to find how long a pendulum should be if we want it to swing back and forth once every 10.0 seconds. The "unknown variable" to be solved for is not by itself on one side of the equal sign. So we must first find the general solution for l.
Many students wish to plug in numbers immediately, without doing the algebraic solution first. these students error in two ways. Most importantly, they miss out on the general pattern of the formula that helps them to understand the process. These students short-circuit the most powerful learning toool involved, and have difficulty progressing to more advanced levels of mathematical thinking. Secondly, many students see the square root sign and believe they must take a square root. In fact, algebra will reveal they must do just the opposite, and find the square of a number (the inverse of finding the square root).
Let's follow the process. First, we must "isolate the radical". We can do this by dividing both sides of the equation by 2p. This yields T/2p = \/( l / g ) .
Then we square both sides, yielding T2/(2p)2 = l / g .
Now we multiply both sides by g. l = gT2/(2p)2
This is the general solution that yields the length
of any pendulum
for any swing period.
Finding a specific solution to an algebraic formula.
Now that we have the general solution, we simply plug in the numbers and calculate the answer to get the specific solution.
l = (9.81 m/s2)(10.0s)2 / 4p2
Checking our units, we see that the seconds-squared in the denominator cancels the seconds-squared in the numerator. This leaves meters, the correct units for length, as required.
Now, using our calculators, we should find that l = 24.8
meters, a very
long pendulum! This should not surprise us too much, however. Our general
formula shows that the length of the pendulum is proportional to
the
square of the swing period, so the length of the pendulum grows
much
faster than the swing period.
Graphing Data Copyright: David Carpenter 2000
Fitting Lines and Curves to Data
Graphs are often used to present information to other people. Scientists use them also to understand information for the first time. If there is a shape to the data when it is graphed, that shape tells the scientist


This data hints at being shaped like a broad upward sloping line if you sort of look at it from a distance [figure 2]. If you draw a line through the center of the broad line, you get the information that the scientist really wants. The position and slope of the center of the line shows the type of formula that represents the data. The breadth of the wide line is a measure of how much error is in the experiment.
Whatever you do, DO NOT CONNECT THE DOTS! [We only connect the dots for that other purpose of graphs, presenting information, or when the data is both very precise and accurate, and when the curve or line that represents the data is smooth and continuous.] Rather, try to cover the data with the thinnest possible "bar", then draw a line down the center of this bar. [See figures 3 and 4.]


Many mathematical functions do not represent straight lines, but curved ones. Frequently this is obvious from the data. The trick here is to make a smooth curved line through the data points, trying to minimize the distance between the data points and the curve. It's basically the same procedure as for straight lines, except with a curved ruler. Stores sell sets of "ship curves" or "French curves" for making smooth curving lines on your graphs. Sometimes plastic rulers set on their edge can be bent to match the curve of the data and used to draw an approximations to the proper curve.
Why do scientists graph data and fit lines or curves to the data? They do this because lines and curves can be formed also by graphing equations. If you find the right equation that matches the data line or curve, that equation is a formula for that data. You can use the formula instead of new experiments and data to predict future results. That's where most of the formulas in scientific papers and in science books come from!
Choosing Axes
Rule #1: In experiments, one variable often depends on another. For example, the distance a car can go depends on how much gasoline is in the gas tank. If there is more gas, the car can go farther. Since the distance depends on the amount of gas, distance is called the “dependent variable”, and is graphed on the vertical or “y” axis. Since the amount of gasoline in the gas tank is chosen freely by the experimenter, the amount of gas is called the “independent variable”, and is graphed on the horizontal or “x” axis.
Rule #2: When time is one of the variables, it is normally chosen to be graphed on the horizontal or “x” axis. The slope of the line or curve on the graph then corresponds to the speed (or rate of change) of the dependent variable.
Choosing Scales
Rule #1: Make each mark or block on the graph worth the same numerical value. If each block represents 0.1 on a given axis, they all should. [Some students will equally space their data along the horizontal axis, regardless of numerical value differences, as is making a comparison bar graph. In so doing, they destroy any ability to see mathematical relationships between the variables represented by the axes. This makes the graph useless, and should be avoided.]
Rule #2: The value of each block must be easily read in decimals, since most data is read that way. If every 3 blocks represents a value of 40, it is difficult to make or read the graph. Each block should represent either tenths, fifths, halves, or if necessary, quarters of a decimal value.
Rule #3: Make the used portion of the graph as
large as
possible. This provides
more precision in making and reading the graph, which allows for great
accuracy. To do
this, it is not necessary for the horizontal axis scale to be the same
as the vertical axis
scale. It may also be beneficial to start each axis near the
smallest data values, moving the
graph origin well off the page. This lets you make the used
portion
of the graph larger
and easier to use. However, sometimes this should be avoided
when you know that the
origin is a valid data point.
Deriving Formulas from
Graphs
Copyright: David
Carpenter 2000
The shape of the line or curve that best fits the data from an experiment determines the type of formula that can be made. This formula will show the relationship between the variable graphed vertically and the one graphed horizontally.
When the data graphs as a straight line, the formula follows the form y = mx + b, where y is the dependent variable from the vertical axis of your graph, x is the independent variable from the horizontal axis of your graph, m is the slope of the line, and b is the y value where the line crosses the y axis. If b = 0, then the line will pass through the origin, and the relationship is called a direct proportion (if the slope is positive, going up from left to right).
The slope can be determined by seeing how much the y value changes for a corresponding change in x. If the y value increases by 6 for every increase in x of 2, the slope is found by dividing the change in y by the change in x. For this example, the slope is 6/2 = 3. In general, we use the formula:
slope = m = Dy/Dx
where the Greek letter delta, D, represents the change in the variable. Dy represents how much the y variable changes for the corresponding change in x, Dx.
If a distance vs. time graph is made to represent the motion of an object moving at constant speed, a linear (straight-line), direct proportion graph is produced.
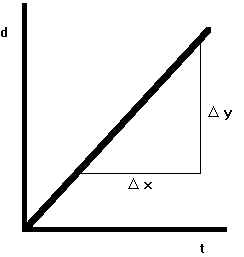
The formula that matches this graph is found from y = mx. Here, y represents distance and can be replaced with d. Likewise x is replaced with t. The slope, m, is therefore Dd/Dt, the definition of speed (v). This yields the equation, d = vt.
If this activity is preceded by an activity such as in the previous section, where the line representing the distance vs. time graph would be found by doing the best possible match to scattered experimental data, than the entire process is complete. A formula is derived from a graph, which is in turn derived from experimental data.
Non-linear formulas
If the data is not easily fit to a straight line, the formula that represents it must also be different. There are two frequent forms.
One of these is
represented
by a graph where
the y value grows faster with increasing x.
The graph curves upward from a straight-line
orientation, with ever increasing slope.
This general form is probably best fit by a
polonomial equation of the form
y
= kxn, or by an exponential
equation
of the form
y = kx.
[k
and n are constants.]
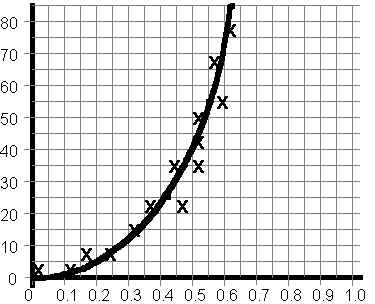
The second
form is represented
by a line that curves down from the y-axis and then
out without ever touching or crossing the
x-axis.
This is the graph of a formula where y
decreases as x increases and vice versa.
This is known as an inverse relation, and is best
fit by an equation of the form y = k/xn.
[k
and n are again constants.]

"Pre-Calculus"
or "Function
Analysis" couses typically teach methods for making a
more precise determination of the formulas
represented
by non-linear graphs. This is
beyond the scope of the Physics 1
curriculum.
Students are, however, expected to
recognize data as representing exponential or
inverse functions in general from the way
that their graphs curve.
Scientific Notation Copyright: David Carpenter 2000
Scientific Notation is a way of writing numbers that makes understanding and using these numbers easier
The
number 360,000
is the product of 36 x 10,000. 10,000 is ten times itself, four
times, or 10 x 10 x 10 x 10
or 104.
360, 000 is therefore
36 x 104. This
last way of
expressing the number is the product of
significant
numerals and a place holder power of
ten. This is scientific notation.
In the standard form of scientific notation, exactly one numeral is to the left of the decimal point. Since 36 is equal to 3.6 x 10, then 360,000 is equal to 3.6 x 10 x 104, or 3.6 x 105.
For other examples:
1730 is equal to 1.73 x 103
9,000,000 is equal to 9 x 106
0.0041 is equal to 4.1 x 1/1000 or
4.1 x 10-3.
Common Errors using Scientific Notation with Calculators
Students often make mistakes when using scientific notation with calculators because many calculators display numbers such as 4 x 103 without the 10. Typically, a calculator display will show 4 x 103 as 4 03. This leads to two different types of common errors.
The first occurs because many calculators do not display the 10, even though they calculate it. Students who then multiply by 10 before using the exponent key will incorrectly make the number 10 times larger than it should be, because the calculator will automatically insert another exponent base of 10.
For example, 3.6 x 105
should be entered as [3] [.] [6] [EE][5], and is displayed as
3.6 05.
[3][.][6][x][1][0][EE][5] is interpreted by the calculator as 3.6 x 10
x 105, or
3.6 x 101+5,
or 3.6 x 106,
ten times too
large. The second common error occurs when students
confuse the [EE] key with the
[yx]
key.
It’s easy to see why this happens, since calculators usually display
scientific
notation in a form that looks like yx.
For example, 2000 is written in scientific notation as 2 x 103. The calculator displays this a 2 03. This looks like 23. But 23 is equal to 2 x 2 x 2, or 8. And 8 does not equal 2000 ! This error is easily avoided if students use the [EE] (or [EXP] on some calculators) key.
Students who borrow unfamiliar
calculators
should always check the calculator
protocol. We can do this by checking how
the calculator deals with a similar problem that
is simple enough for us to solve in our
heads.
The way of entering the problem into the
calculator that yields a correct
answer for the
simple problem should also be correct for
the more complicated problem. If a method
doesn’t solve the simple problem correctly, it
won’t work for the real problem
either!
Always use this simple procedure. In this way,
most “calculator errors” can be avoided.
Dimensional
Analysis
Copyright: David
Carpenter 2000
Dimensional analysis is the process of doing a mathematical operation (such as multiplying or dividing) with units. The rules are the same as for algebraic variables.
Therefore: kg m2/s2/m2 = kg/s2 because m2 can be factored out of both the numerator and the denominator.
[ kg = kilogram, m = meter, s = second, N = newton ]
Dimensional analysis helps us to get the correct units at the end of a problem.
In Newton's 2nd Law, a = F/m, where a is the acceleration of an object, F is the applied force causing that acceleration, and m is the mass of the object. The units of acceleration should be m/s2. However, if we actually solve a problem where a force of 7.0 N is applied to a 2.0 kg object, we find that
a =F/m = 7.0 N/ 2.0 kg = 3.5 N/kg.
We wanted our units to be m/s2, but instead we have N/kg. Are they the same? Or have we revealed a mistake in our method?
If we remember the definition of a newton (N) of force, we know that 1 N = 1 kg m/s2. This implies that 3.5 N/kg is really the same as 3.5 kg m/s2 / kg. The kg in the numerator cancels out the kg in the denominator, leaving the expected m/s2. Thus we end up with the correct units. [We also get confirmation that are formula and method is likely to be correct as well.]
Dimensional Analysis is also important
when doing
unit conversions, as in converting
12 km/h/s, representing an increase of speed
by 12 kph every second, to units of m/s2.
Since 1000 m = 1 km and 1 hour =
3600 seconds,
multiplying by (1000m/1 km)
doesn't
change the value of the number, because (1000m/1
km) = 1. Also, (1 h/3600 s)
= 1.
So:
12 km/h/s = 12 km/(h*s) = (12km/h*s)(1000m/1
km)(1 h/3600
s) = 3.3 m/s2.
Vector Addition in Two
Dimensions
Copyright: David
Carpenter 2000
vector: a quantity with both size ("magnitude" or amount) and direction.
If two cars collide, one moving at 60 kph and the other at 55 kph, is it a serious accident? The answer to this question does not depend only on their speeds, but also on their directions. A head-on collision between these two cars would be serious indeed. But if the 60 kph car overtakes the 55 kph car from the rear, it will only be a "fender-bender".
To study the effects of physical
quantities where
direction is important, we need a
mathematics of vectors. Some of the basic
rules for this will be outlined here.
Coordinate Transformations
Transformation Equations
polar
coordinates
=> rectangular coordinates
x = r cosf
y = r sinf
rectangular coordinates => polar
coordinates
r = \/(x2 + y2)
f = arctan(y/x)
Suppose a vector is given that is of length 10 and at an angle of 30o (counter-clockwise from the positive x-axis). To make this example more real, lets assume that it is a force vector, representing a force of 10.0 N. This force vector would push an object both upward and to the right. How much upward and how much to the right? To find out, we use the transformation equations for converting from polar to rectangular coordinates.
How much to the right can be calculated from x = r cosf, where r = 10.0 N and f = 30o.
Then x = (10.0 N) cos(30o) = (10.0 N)(0.8660) = 8.66 N is the amount to the right.
And from y = r sinf, y = (10.0 N) sin(30o) = (10.0 N)(0.500) = 5.00 N is the amount upward.
To understand both the purpose and procedure in the above example, I have mixed coordinate and vector notation. Since the example deals with a force, the logical variable representing this should be F. To label the corresponding parts of F in the x, y and r directions, we can use the coordinate labels as subscripts. Thus we get Fx, Fy, and Fr.
Then x = r cosf becomes Fx = Fr cosf. Calculating with these is exactly the same. Only the names of the variables have been changed.
[Likewise, the
corresponding transformation
equation for velocity vectors becomes vx =
vrcosf.
If we
are simply transforming
coordinates
on a graph, we can use the original version of the equations.]
Vector Resolution
Vector resolution is the process of breaking apart (resolving) a vector into perpendicular parts. In many cases, the process is identical to changing from polar to rectangular coordinates.
Suppose we have a vector of length 8 at 30o.

The x-component of this vector can be
found from
x
= r cosf = 8cos30o
= 8(.8660) = 6.9.
The y-component of this vector can be found from
y = r sinf = 8sin30o
= 8(.5000) = 4.
Thus a vector of length 8 at 30o can
be resolved into an x-component vector of length 6.9
and a y-component vector of length 4.
Vector Addition
Vector addition is the process of combining the effects of two or more vectors. There are two common methods. One method involves resolving all the vectors into their x and y components, adding and subtracting these components, and then transforming the answer back into polar coordinates. This is the method to be discussed here. [The second method involves a coordinate rotation, followed by use of the law of cosines, followed by a return rotation back to the original coordinates.]
Suppose the vector from the above example is added to (or combined with) a vector with r = 6 at 45o. Then this new vector can also be resolved into two component vectors, x2 and y2. [The original vectors components become x1 and y1.]
Then x2 = r2 cosf2 = 6cos45o = 4.2 and y2 = r2 sinf2 = 4.2.
If we now add the x-components, we will
get the
x-component of the "resultant". This
resultant, R, is the "vector sum" of the two
original vectors.
xR = x1 + x2
= 6.9 + 4.2 = 11.1
Likewise for the y-components,
yR = y1 + y2
= 4 + 4.2 = 8.2
Converting this resultant to polar
coordinates:
r = \/(x2
+ y2) = \/(11.12
+ 8.92) = 14.2
f = arctan(y/x)
= arctan(8.9/11.1)
= 39o
If these are all force vectors, then the resultant can be expressed as FNET = 14.2 N @ 39o.
Example Problem:

Add the two force vectors in the diagram to obtain their resultant vector. First label the two vectors: let's name the 4.0 N vector number 1, and the other number 2, using these designations as subscripts throughout. Then r1 = 4.0 N, and F1 = 4.0 N @ 50o.
Then using the transformation equations:
x1 = r1 cosf1
= 4.0cos50o =
2.57
y1 = r1 sinf1
= 4.0sin50o = 3.06
x2 = r2 cosf2
= -5.0cos30o = -4.33
y2 = r2 sinf2
= 5.0sin30o = 2.50
xR = x1 + x2
_________________________________________________________
yR = y1 + y2
xR = -1.76
yR = 5.56
Dropping the negatives and substituting xR and yR into the rectangular-to-polar transformation equations.
r = \/(1.762
+ 5.562) = 5.83
f = arctan(5.56/1.76)
= 72o
However, xR is negative and yR is positive, indicating that the resultant is in the second quadrant, where the reference angle q (measured counter-clockwise from the positive x-axis) is q = 180o - f.
This yields q
= 180o - 72o = 108o, and FNET
= 5.83 N @ 108o.
Precision, Accuracy,
Significant
Figures and Rounding
Copyright: David Carpenter 2000
Significant Figures
There are two types of numerals
in ordinary
numbers: significant figures and place
holding zeros. Place holding zeros are
the zeros that go away when you convert to
scientific notation.
34,000 = 3.4 x 104 0.0078 = 7.8 x 10-3
Not all zeros are place holding zeros, some are significant, as in the zero in 307. Conversion to scientific notation yields 3.07 x 102. All non-zero numerals are significant.
Examples of numbers with 2 significant figures:
48 .0032 5.7 5200
Examples of numbers with 5 significant figures:
23,789 54,043 3.9009 .0034021
Some numbers are considered to have an infinite number of significant figures, such as those that are part of exact formulas.
C = 2pr v = \/(2ad)
In both of these expressions, the 2
represents
an exact 2, with an infinite number of
significant figures. [These exact formula
values are recognizable from variable values by
the fact that they are not found from
measurements.]
Other numbers are limited by the
precision of the measurement method, or of the
calculating device. Slide rules were
typically only accurate to about three
significant
figures, modern calculators usually
display eight to ten significant figures.
[But the value displayed by the calculator is only as
precise as the numbers used in the
calculation.
An “about” number can not be multiplied
by an “about” number to get an “exact” number,
no matter what the calculator displays!]
The significant figures possible with a measuring
device depend on the size and marking of
the scale.
Rules for keeping the correct number of significant figures:
1. For addition and subtraction, the answer should be no more precise than the least precise value being added or subtracted.
45.387
5.8 <== least precise number, to tenths place
.092
+ .23
51.5 <== answer to tenths place
2. For multiplication and division, the answer should have no more significant figures than the term with the least number of significant figures.
(4892 x 38 x 521)/389 = 250,000
^
^
2
places
2 places
For numbers such as 250,000, it is impossible to be sure whether or not the zeros are significant or not, except by context, or by denotation with either a bar below significant zeros, or by ending with a decimal point. Non-zero numbers in parenthesis to the right of a decimal may not be significant.
Examples:
27
2 significant figures.
421
3 significant figures.
402
3 significant figures.
680
at least 2 significant figures, maybe 3, judge from context.
680.
3 significant figures, the decimal point shows that the zero is
significant.
23.2
3 significant figures.
23.20
4 significant figures, this zero is unnecessary if not significant.
0.00048
2 significant figures.
0.0005
1 significant figure.
4.82(527)
3 significant figures, and the measurement precision exceeds its
accuracy.
Precision, Accuracy and Rounding
Many people think that these two terms mean the same thing, but they do not.
Precision is how fine of a
measurement that
the measuring instrument is marked
off for. A typical meter stick or metric
ruler has millimeter marks as its smallest marking.
A yard stick’s smallest marks may be 1/8
inches.
By estimating between the marks we can
measure to half millimeters and to 1/16 of
an inch with these tools. This is the limit of our
precision with meter sticks and yard
sticks.
But if we use these measuring tools in a
sloppy fashion, say by letting the position of
the end slip, the measurements will not be
accurate to anywhere near a millimeter or an
1/8 of an inch.
Accuracy is how correct or true that a measurement is. If I estimate the width of a room to be 4 meters, and it is, than that is an accurate, but not precise measurement. If I let the ends slip on my meterstick, and measure the width of the room to be 4.2165 meters, that is a precise but inaccurate measurement. Only if I am very careful, I can get an accuracy that equals my precision when using a meter stick.
This all becomes very important
when considering
the validity and economics of
scientific research. Often it is easy to
make accurate measurements such as when using a
ruler to measure a small rectangular block.
Several repeated measurements are likely to
read the exact same value. If you repeated
the measurement a thousand times, you would
achieve no greater accuracy. You would
only waste your time (and perhaps, your
employer’s money).
But equally often we try to
measure things
that are difficult to measure accurately.
An example might be the measuring of the length
of a room with an ordinary ruler. It is
very difficult not to make errors of a couple
of millimeters (or of an 1/8 inch or so) when
moving the ruler to position after
position.
We might try to make our final measurement
to a fraction of a millimeter, but in fact, our
answer maybe several centimeters off! Now if
we made the measurement 1000 times and averaged
the results, we might improve our
accuracy to only one or two centimeters.
Circumstance will determine whether or this
repetition is worthwhile. But accuracy
can only be improved by repeating measurements
and averaging only when the precision is finer
than the accuracy.
Another example of when repeating and averaging measurements is when using a stopwatch. The typical digital stopwatch is more precise than it is accurate. The typical stopwatch displays with a precision of 1/100 of a second intervals. But the human reaction time for starting and stopping the watch is about 0.2 seconds. Since the precision is 20 times finer than the accuracy, repeating and averaging can yield more accuracy.
When reporting data, it is important not to report more accuracy than you have. People who read your reports will judge your accuracy based on the number of significant figures in your data. It is therefore imperative that you round off numbers to the last place value that is known to be accurate.
Calculations and conversions can
never increase
your accuracy, although in
everyday life people often make this
mistake.
The most amusing to me is to find 4 inch
paint brushes labeled in metric as 101.6
mm.
Some calculator-happy person at the factory
did a direct conversion and did not round off,
as though every 4 inch paint brush on the
shelf was exactly four inches wide to the nearest
1/254
of an inch (not a single spread or
bent hair in the lot)! In scientific
literature,
this would be a deception and a lie. The
proper thing to do would be to round off to the
accuracy of the measurement. In this
case, they are 100 mm brushes.
A
similar misrepresentation
occurs with normal body temperature. A healthy
adult’s body temperature is about 37o
Celsius, but varies substantially about this value.
Even at two significant figures, this is an
approximation.
A calculator conversion of 37o
Celsius to Fahrenheit yields the familiar 98.6oF.
Magically, a number that was
approximate to two significant figures becomes
accurate to three significant figures simply
by converting to a different measuring
system?
I don’t think so! [What would happen if
you converted back and forth several
times???]
To quote 98.6oF is a common, but
dishonest, misrepresentation of the
accuracy.
Normal body temperature is about 99oF
(two significant figures).
Applied Problem
Links
return to Hayes Physics