This chapter, like all the others, has just two ideas in it; the second one builds on the first. One is kind of complicated to understand; the other isn't bad at all. Let's take the harder one first.

Actually, a sampling distribution is only hard to understand when you're reading the definition. If you see one in action, the whole thing gets clearer. Let's start with that pesky definition, then look at an actual sampling distribution, then we'll look at the definition once again. You'll be surprised how much easier these things are to understand once you've made one.

The Definition: A sampling distribution is a frequency distribution of values of a statistic computed for all possible samples of size N drawn from a population, sampling with replacement. As a rule, sampling distributions are theoretical distributions.

See what I mean? I'll bet this didn't make much sense to you. Let's take it one step at a time.

The way we usually sample is without replacement; you draw out a case and put it in your sample, then draw out another, etc. Once a case is drawn, it can't be drawn again because it is removed from the population from which you're sampling. Well, sampling with replacement is different in that after you draw a case out, you then place it back in the population so that you might draw it again--and again--and again. To make a sampling distribution, you sample with replacement.

You'll draw all possible samples of a given size from the population; sample size is (as usual) N. This means you're drawing a sample for each possible combination of N cases in the population.

Once you've drawn all these samples, you compute some statistic, often the mean, for each sample. Then you make a frequency distribution of all the means (or whatever) you found for all the samples you drew. This frequency distribution is the sampling distribution.

Making a Sampling Distribution of the Mean: The definition was the hard part; now let's look at an actual sampling distribution from a very small population (It's a nightmare doing one from a big population, which is why these things are theoretical, not empirical; who'd want to do a real one?) and see what all this is about. Let's use for our example the one given in Comprehension Check 5.3 on page 124 in your textbook. There's a typo in this problem; it says there are five cases in the population, but there are really only four. Here's what your author tells you about this problem (with my correction):

It helps to be systematic about all of this:

Suppose the first case you draw has an IQ of 100. Write that down, then put the case back into the bag (replacement), stir it up, and draw again. Suppose you draw 100 again. This is legal when sampling with replacement; so you have a possible sample here. The sample contains 2 cases: 100 and 100. Make a note.

Now suppose you draw 100 first, put it back in, and draw 105. This is your second possible sample: 100 and 105. (You should note here that the order of the draw doesn't really matter; it's handy when I'm trying to describe to you what might happen, but in fact whether the 100 or the 105 is drawn first is irrelevant. This is still just one possibility; if we drew 105 first, then 100, this would be a repeat of what I've just described, not a new possible sample. Only the content of each sample matters, not the order of draw.)

So now suppose you draw 100 first, put it back in, then draw 110. Third possible sample: 100 and 110.

And now suppose you draw 100 first, put it back in, then draw 115. Fourth sample: 100 and 115.

Now we've exhausted all the possible things that could happen when one case drawn is 100; the other one could be 100 (again), 105, 110, or 115. So let's move on to the possibilities when 105 is one of the cases drawn.

Well, if you draw 105 first, then put the case back in and draw again, you might draw out 100 next. This sample, 105 and 100, is identical to the second sample you drew above (100 and 105). Not unique, so it is a duplicate and doesn't count as one of your possible combinations. Already noted.

What if you draw 105 first, put it back in, then draw 105 again? This could happen when sampling with replacement, couldn't it? It's a legitimate possibility, so we have another possible sample here: 105 and 105.

We could draw 105, then 110. New possibility: 105 and 110.

Then there's 105 and 115. And that's all the possibilities when 105 is one of the cases drawn.

When you start figuring out combinations with 110, remember that you've already had the combination 100 and 110, as well as 105 and 110. That leaves only 110 and 110, 110 and 115. And then when you work on 115, remember we've already drawn 115 and 100, 115 and 105, and 115 and 110. That leaves 115 and 115--your last possible sample, bringing us to a grand total of ten possible samples.

And that should be that! Let's collect in one place all the possible samples of size N=2 you can draw from the population 100, 105, 110, and 115. Here they are:

Now, what was the next step? Since this is a sampling distribution of the mean, we need to compute the mean for each sample. Here are our samples again, this time with the means added below each in bold print:

So how are we doing? We've drawn our samples in the approved manner. We computed a mean for each sample. What's left to do? Well, a sampling distribution is a frequency distribution of these means, so I guess we have to make a frequency distribution. Here goes:

Not very exciting, is it? Let's take a look at the distribution graphed:

Now you try constructing the sampling distribution of the mean for samples of size N=3. This means you go through all the same steps: draw all possible samples (this time N=3) from this population, sampling with replacement; compute the mean for each sample; and set up a frequency distribution of the means. Don't forget to graph your result. HINT: you should have 20 samples. (You should know in advance that there is a point to all of this; I'm not just torturing you.) Don't look on until you've finished; the answers follow.

The Definition Revisited: OK, let's return to that definition of a sampling distribution. It should make a lot more sense, now that you've constructed two of them. Here it is again:

A sampling distribution is a frequency distribution of values of a statistic computed for all possible samples of size N drawn from a population, sampling with replacement.

All right, this is a frequency distribution of values of a statistic, the mean. We computed the means for all possible samples of a certain size (N=2 for the first one, N=3 for the second); and we sampled with replacement. There it is; it does make more sense now, doesn't it?

Characteristics of Sampling Distributions: So now, having done all this work, I want you to begin noticing some things.

Shape: The first is the general shapes of the two graphs you've drawn. They're both kind of skimpy on plotted points, but they sort of resemble the normal distribution we studied in the last chapter--symmetrical, bell-shaped, unimodal. The second distribution you drew is closer to normal than the first one; that's because you have more and larger samples. While our samples were too small to get a really normal distribution, large samples do give us just that. This brings us to the first rule of sampling distributions: if the sample size is large enough sampling distributions are ALWAYS normal, no matter what the shape of the original population's distribution. The more non-normal the original population, the bigger the samples have to be in order to see a normally-shaped sampling distribution; but generally samples of 50 or more give pretty normal sampling distributions, no matter what the shape of the population distribution. Think about the shape of the population distribution for the examples you just did; it's not even sort of normal:

Despite this, the sampling distributions at least try for normal.

This is a handy characteristic of sampling distributions. It means all the things you learned about normal distributions (including areas between the mean and various points found in the Table of Areas) are also true of sampling distributions.

Mean: Another thing you might notice just by eyeballing it, although it also works out mathematically if you want to take the time, is that the mean of the sampling distribution of the mean is the same as the mean of the original population. This is true no matter how small your samples; it even works for your little population and samples. Check it out with the two examples you did above.

Standard Deviation: You can tell at a glance that the means of all the samples you drew are not the same. Even though they were drawn from the same population and even though there was nothing wrong with your sampling technique, the means are somewhat different. Why? Our old friend, sampling error. Remember that the act of sampling produces error, simply because samples don't contain all the cases the population does. (If they did, there wouldn't be much point in sampling, would there?)

The issue here is that the sample means show variability--differences from one to another. The way we get a feel for the variability of a sampling distribution is to compute variance and then standard deviation for the distribution. Here's where the words start to tangle us up; we're talking about computing the standard deviation of the sampling distribution of the mean. Try saying that three times fast. We're in luck, however, because statisticians have come up with a slightly easier to remember name for this; it is standard error of the mean. Its symbol is . The standard error of the mean IS the standard deviation of the sampling distribution we just constructed. It is the roughly the average deviation of all those sample means from the true population mean (which is the mean of the sampling distribution too).

AND, the good news is that we don't have to go through all the usual steps from Chapter 3 to find this number. To compute the standard error of the mean, we need to know the population standard deviation and the sample size. With these, we use the following formula to find standard error of the mean:

Now you'll notice by looking at the formula that the standard error of the mean gets larger when the population standard deviation is larger. Makes sense when you think about it that the more variable the population, the more variable will be the means of samples drawn from it. You can also tell by looking at the formula that the standard error of the mean gets smaller when the sample size is larger. Again this makes sense, since you divide by the square root of N.

Since variability in the sampling distribution is an indication of how much sampling error there is (because it is caused by sampling error), the smaller it is, the better. In general, we don't like error, whatever the cause, because it decreases the accuracy of our work. So anything that makes it smaller is a good thing. We can't do anything about the size of the population standard deviation; here a high standard error is simply a reflection of a highly variable population. But we can do a great deal about sample size when designing research; bigger samples are better. You'll hear this many times during this course. In general, when doing research, the larger the sample size, the better the result.

Well, this is all well and good if we happen to know the population standard deviation. What if we don't? Can you think of an alternative? How about a good estimate of the population standard deviation? What would that be? Think Chapter 3 here: we could use the corrected standard deviation, couldn't we? It's intended as an estimate of the population figure, isn't it? (You see, there is a purpose to everything if you wait long enough.) When we use a corrected standard deviation in our computation, we end up with an estimated standard error of the mean. Here's the formula:

Central Limit Theorem: These three characteristics of sampling distributions--the normal shape, the mean equal to the population mean, and the procedure for computing their standard deviations--are all gathered into a rule called the central limit theorem. This theorem describes the shape, the mean, and the variability of a sampling distribution.

Sampling Distribution of the Proportion: A proportion is simply the decimal value of the fraction of cases in a particular category. For example, if ½ of cases are Catholic, the proportion of Catholics is 0.5. You know that from the work you did in Chapter 4.

Let's think about proportions where there are only two categories into which cases can fit, for example, married and unmarried, men and women, drivers and non-drivers. Say we assign a value of 1 to married and 0 to unmarried. Then the proportion of married people is the same as the mean of the sample. Let me show you what I mean. Here's your sample of 10, with a value of 1 or 0 assigned to each case, based on whether the cases are married:

The number of married cases is 6. The proportion of married cases (p) is . Now compute the mean score for the sample.

1 + 1 + 1 + 0 + 1 + 0 + 1 + 0 + 0 + 1 = 6

The proportion and the mean are the same thing! This means that if we make a sampling distribution of the proportion, we are really computing a sampling distribution of the mean. That means that all the things we just said about the sampling distribution of the mean with the central limit theorem are also true of the sampling distribution of the proportion. Same thing, precisely! This comes up later. (It also means that we can apply all the stuff on confidence intervals which follows to nominal scale variables, as long as they have only two categories.)

Working with Proportions: For the record, p represents the proportion of cases assigned a value of 1. The proportion of cases assigned a value of 0 is designated as q, and should be equal to 1 - p. Go back to our example with married and unmarried people. The mean (proportion of cases assigned a 1) or p was 0.6. That means that the proportion of cases assigned a 0, q, should be 1 - p or 1 - 0.6 = 0.4. Go ahead and work out the proportion of cases that were unmarried; you'll find it does indeed equal 0.4.

Here's another handy bit of information. You can find the variance (s²) of the group using the following formula:

This will save a lot of time over the traditional method for computing variance. Do remember that variance is NOT standard deviation (s), but the square of standard deviation (s²). More trouble is caused by people mixing up variance and standard deviation than I can even describe. Don't be one of those people mixing them up.

Have you ever been watching the evening news and heard the results of a poll? You know, they ask 2000 Americans, "Are you in favor of the Republican tax plan?" Then they report the results as 47% in favor, 44% opposed, 9% undecided. Well, if you look closely at the bottom of the screen as the results are posted, you'll see a statement that the results are reported as accurate plus or minus three per cent.

This does not mean that the pollsters are unsure exactly what per cent of the 2000 people are "in favor" or "opposed." Those numbers are reported correctly. What it does means is that the only way to find out what all Americans think of the tax plan is to ask all Americans, not just 2000 of them. Of course, asking all Americans is not generally a reasonable task; this is why we rely on samples in the first place. Nonetheless, a sample will never give us a perfectly accurate picture of the population, no matter how carefully it is drawn--sampling error again. However, the statisticians who did the poll of 2000 people are pretty darned sure that the real number who favor the tax plan is within three percentage points of the 47% they reported. How sure? Generally 95% sure. So there is a 95% probability that the actual number of all Americans who favor the plan is between 44 and 50%--that's 47%3%. That range--from 44-50%--is what's known as a confidence interval. The level of confidence for that particular confidence interval is 95%, which is kind of a standard; most statistical results are given at that level--if it's different, they'll say so.

Confidence Intervals: So a confidence interval is a mathematical estimate of the likelihood and degree to which you're wrong when you generalize from a sample to a population. This has to do with inferential statistics--using sample data to draw conclusions about the population from which the samples are drawn. We know that these sorts of conclusions are never (except by pure dumb luck) exactly right--sampling error rears its ugly head again.

The confidence interval is a range constructed around your sample mean, which has a known probability of containing the actual population mean. It is generally not reported as a range like 44-50%, but is most often shown like the poll results for the Republican tax plan. The sample mean is reported along with a margin of error, which constitutes the confidence interval.

Interval Estimation: Part of being honest with statistics is to admit you could be wrong, then to estimate the likelihood you're wrong, and to estimate how far wrong you most likely are. The process of figuring out at some level of confidence (usually 95%) how far wrong you may be is called interval estimation. This is the procedure you're about to learn. And compared to sampling distributions, it's a breeze.

The 95% Confidence Interval for the Population Mean: Theory. Let's start with the most commonly used confidence interval, 95%. Think about the sampling distribution of the mean. We know it includes the means of every possible sample of size N. We also know its mean is the same as the population mean. Now consider how we might define an area that includes 95% of the area under the curve--right in the middle. It would look like this:

This blue area would include the means of 95% of the possible samples you could draw from the population. Only 5% of sample means are outside the area--2.5% in each "tail."

How far away from the population mean would we have to go to include this blue area? Well we can figure it out in terms of z-scores by using the Table of Areas, couldn't we? Think about what we're working with; we know the areas in each portion of the graph, don't we? 0.9500 is blue--0.4750 on either side of the mean; then there is 0.0250 in each tail.

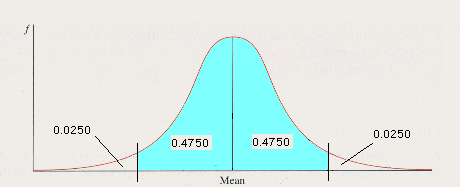
So we can look in the Table of Areas in the (B) Column for 0.4750 or in the (C) Column for 0.0250. Whatever z-score matches these areas defines the blue area above, doesn't it? Look it up. You should find a z-score of 1.96, which means that z=+1.96 defines the right-hand border of our blue area and z=-1.96 defines the left-hand one. This means that the blue area is between 1.96 standard deviations below and 1.96 standard deviations above the population mean.

Now, follow this reasoning carefully. This is a sampling distribution, so a standard deviation is a standard error. In a sampling distribution of the mean, 95% of sample means are found within 1.96 standard errors of the population mean; that's what we just figured out, isn't it? Therefore, if we draw an area around each individual sample mean in the distribution from 1.96 standard errors below it to 1.96 standard errors above it, for 95% of sample means that area would include the population mean.

You can demonstrate this for yourself. Take a piece of paper and draw a line on it exactly as long as the baseline under our 95% blue center area on the diagram above. Cut the paper off to the length of that line and fold it in half; when you open it again, the crease you've make marks the center point. This center point represents the sample mean. Now slide the paper back and forth along the baseline, noting when the sample mean (center point) is inside the 95% area and when it is not. Do you see that as long as the sample mean stays inside the blue area, one end or the other of your paper also overlaps the population mean? So as long as your sample mean stays inside the blue 95% area, your paper, which represents the confidence interval, overlaps the population mean. And 95% of the possible sample means you can get are inside the blue area. This demonstrates that an area sized to reach from 1.96 standard errors above the sample mean to 1.96 standard errors below the sample mean has a 95% chance in including the population mean.

So, if we build a confidence interval around our particular sample mean that is 1.96 standard errors wide on either side of it, we have a 95% chance that that confidence interval will include the population mean. Think about the definition of a confidence interval-- a range constructed around your sample mean, which has a known probability of containing the actual population mean. There we go! The range will be 1.96 standard errors; it will be constructed around the sample mean; and it will have a known (95%) probability of containing the population mean. That's what we need.

The 95% Confidence Interval for the Population Mean: Practice. So, how do we go about actually defining this 95% confidence interval? Let's look at an example:

Say you've used the College Readiness Inventory to test the college readiness of 100 high school seniors. On the CRI, the population standard deviation is 7. Our sample showed a mean score of 37. What will we do about constructing the 95% confidence interval?

Well, we know we need to go 1.96 standard errors to either side of our sample mean. To do this we need to know the sample mean, which is given as 37, and we need to know how big a standard error is. You have the formula for computing standard error of the mean. Here it is again:

So to compute standard error of the mean, we also need to know the population standard deviation, which is given as 7, and the size of N, which is given as 100. Let's solve it:

And now we need to figure out how far above and below the sample mean we go for 1.96 standard errors:

So our confidence interval is from 1.37 points below the sample mean to 1.37 points above it. As mentioned above, the standard method for writing confidence intervals is to list the sample mean, then the size of the confidence interval, like this:

Even though we don't write the confidence interval as a range of values, it's good to keep in mind just what this means. We're saying that we're 95% sure the actual population mean is between 35.63 and 38.37. That's pretty close!

If you want a formula for figuring out 95% confidence intervals, it would look like this:

95% confidence interval =

The 90% Confidence Interval for the Population Mean: You can figure out how to construct a 90% confidence interval in the very same way you figured out the 95% interval. If we draw a sampling distribution of the mean, mark 90% of the area under the curve, and label the areas for each section, we can then use the Table of Areas to find the z-score we need:

When you look up the z-score we need for this level of confidence, you find there is a tie between z=1.64 and z=1.65. Time for another executive decision; you should know that the generally accepted choice is 1.65, so that's what we'll use.

So to construct the 90% confidence interval around our sample mean of 37 in the CRI example above, we do the following:

Same standard error as before, isn't it? But it should be, shouldn't it? We're using the same sample from the same population; the population standard deviation and sample size haven't changed. The only difference in constructing the 90% confidence interval from the way you constructed the 95% confidence interval is that the number of standard errors--the z-score--will be smaller.

So we figure out how big 1.65 standard errors are, and we have the interval size all worked out. This means the interval size is 1.16, so the 90% confidence interval will be 371.16. If you want a formula, it would be the following:

The 99% Confidence Interval for the Population Mean: Now try on your own to figure out the 99% confidence interval for our CRI example. The work to demonstrate the answer follows:

The Table of Areas gives the z-score which has 0.4950 in the (B) Column and 0.0050 in the (C) Column as 2.58--actually here's another tie between 2.57 and 2.58; convention has us using 2.58. So the formula, if you need one, for finding the 99% confidence interval is as follows:

99% confidence interval =

And the confidence interval for our example is 371.81.

Other Levels of Confidence: The most frequently used levels of confidence are the three for which you've just found z-scores. You can use the Table of Areas to find the z-scores for any other level of confidence you need. Just follow the same steps:

1) Turn the level of confidence from a percent into a proportion and split it in half.

2) Look up the z-score for that result in Column (B) of the Table of Areas.

Interval Estimation Using Estimated Standard Error of the Mean: All of the examples thus far deal with populations whose standard deviation is known; but, in real life, we know this is often not the case. We've already talked about how to compute standard error when the population standard deviation isn't known: that's when you use corrected standard deviation to compute an estimated standard error of the mean.

Try this example: On the Physicians' Compassion Index, a sample of 62 general practitioners achieved a mean score of 79, with a standard deviation of 8. Construct the 95% confidence interval for the population mean. The answer follows.

First we need to estimate the standard error of the mean; this will be an estimate because we don't know the population standard deviation, so will have to use an estimated population figure. This requires correcting the sample standard deviation, which is given as 8. How do we do this?

Remember that standard deviations cannot be corrected directly; you must find the variance, correct that, then find the corrected standard deviation from that. There is no shortcut for this procedure. Well, computing the variance (s²) from the standard deviation (s) is fairly straightforward; we simply square standard deviation. 8² = 64. Now the way to correct variance is to divide the sum of squares (which we divided by N to get variance) by N - 1. How do we get the SS? If we divided SS by N to get s², then multiplying s² by N should get us back to SS, shouldn't it? (64)(62) = 3968. Now that we have SS, we just need to divide by N - 1, or 61, to find corrected variance; the result is 65.

There is a formula for correcting variance, which will be provided to you when you take the test. It's simply a mathematical statement of the steps we just finished. Here it is:

The square root of this is corrected standard deviation: 8.06. This gives us the number we need to put into the formula for estimated standard error of the mean:

And now, with our estimated standard error of the mean, we can construct the confidence interval; it is 792.00.

The most common problems I see with this procedure are related to three things. The first is confusing variance and standard deviation--happens all the time; I've already warned you about this, but another reminder is still a good idea. The second comes with forgetting to use a corrected standard deviation. The sample standard deviation is NOT the same and it will give you an incorrect answer. The third problem is from trying to correct the standard deviation directly. It CAN'T BE DONE. You simply must square it to get variance and correct that.

Interval Estimation When N is Small: We've been operating under the assumption that our sampling distribution is a normal distribution. That's why we've been getting z-scores from the Table of Areas; its full name is Table of Areas Under the Normal Curve. That means the values we've been using work only if the curve for which we're getting areas is a normal one, doesn't it? Think back to the Central Limit Theorem; it says the sampling distribution is normal only when samples are large enough. How large is "large enough?" It also tells us that the magic number is N = 50. Sampling distributions flatten out for smaller sample sizes--the smaller the sample, the flatter the curve.

What does that mean for us? Well, let's take a look at a flattened curve:

To get 95% of the area under this curve, we're going to have to go out from the mean further than 1.96 standard errors--we need a bigger z-score. Using the table of areas to get our z-score will underestimate the size of the confidence interval, giving us a narrower interval than we should have. We need a new source for a z-score, one that takes into account this flattening effect of smaller samples on the sampling distribution. Fortunately there is such a source.

Look in Appendix B of your textbook for Table 2: Critical Values of t. This table, among other things, gives us z-scores from these flattened curves, but you have to know how to read it.

Turn to page 403 in the textbook and use it to follow this discussion. To enter this table, you need a level of significance, so you know which column to use in finding your z-score. Note that this table uses significance level instead of confidence level; no matter, they're related. Significance is the proportion of the area under the curve found in the tails outside the confidence area we colored in blue when we did our examples. So you know how to find this: for a 95% confidence level 0.9500 of the area was blue and 0.0500 was found in the tails. So the significance level is 0.05. For a 90% confidence level, the significance level is 0.10; and for 99%, it is 0.01. Note that there are two sets of column headings, one for the One-Tail Test and one for the Two-Tail Test. You don't need to worry about One- and Two-Tail Tests until we get to Chapter 6; but since we're interested in the total area under both tails, we'll use the headings that go with Two-Tail Tests.

The other piece of information you need to enter this table is degrees of freedom (df), so you know which row of the table to read. Degrees of freedom is directly related to sample size (This is how we account for the fact that different Ns give us different degrees of flattening.); df = N - 1. So if your sample size is 12, df = 11. Notice that for dfs over 30, the table lists numbers at intervals--40, 60, etc. If you need a df that doesn't appear on the table, the rule is that you go to the next lower number--which is actually higher up on the table. So if your N = 40, making your df = 39, you must use df = 30 to enter the table. No matter that 39 is closer to 40 than 30, the rule says you must use the next lower number listed.

So to find your z-score, you enter the table at the proper significance level and degrees of freedom, follow the correct row and column to the point at which they intersect, and use as a z-score the number you find at the intersection. Let's do a couple of examples:

If your sample on the CRI had been N = 25, then to construct the 95% confidence interval, you'd enter the t Table at the 0.05 significance level (Remember, we're looking under Two-Tail Tests.) and df = N - 1 = 24. The value of t you will use for your z-score is 2.064. To construct the confidence interval you will use 2.064 in place of the 1.96 from the Table of Areas you used when sample size was N = 100. If you need a formula, here it is:

95% confidence interval =

Note that the confidence interval is wider, as it should be with a flatter sampling distribution.

For the 90% confidence interval, you would enter the table at the 0.10 significance level and df = 24 to find a z-score of 1.711; the confidence interval would be 371.20. And for the 99% confidence interval, you enter the table at 0.01 and df = 24 to find 2.797; the confidence interval is 371.96.

Interval Estimation When N is Small AND the Population Standard Deviation is Unknown: This can happen, and it involves remembering to deal with both problems, one at a time. You must go to the t Table for your z-score; and you must correct the sample standard deviation by the method just shown, using it to find the estimated standard error of the mean.

The size of a confidence interval is of interest. Ideally, the interval would be small; that would mean that our results were highly accurate. For example, in the poll mentioned earlier, it would be great if pollsters could report to the public that 47% of Americans favored the Republican tax plan with a margin of error of only 0.5%. That would mean that the actual per cent of the population favoring the plan is between 46.5 and 47.5%. This is highly precise information!

On the other hand, what if the poll results had a margin of error of 25%? That would mean that the actual per cent of the population favoring the tax plan is between 22 and 72%--hardly useful information! Most of us could make that good a prediction by sheer guesswork. Generally speaking, the smaller the confidence interval, the better. Of course, since there are no free lunches in statistics, there are trade-offs; to attain a really narrow confidence interval, you must give something up. Let's take a look and see what this means.

Level of Confidence: Look at the differences in width among the confidence intervals you've constructed for the CRI example: At 99%, the interval is 3.62 (2 X 1.81) points in width; at 95%, it is 2.74 (2 X 1.37) points; and at 90%, it is 2.32 (2 X 1.16).

It looks as though one way to get a narrower interval is to go with a lower level of confidence. So, if we don't mind being less sure of ourselves, we can get a very narrow interval indeed. For example, if we want a margin of error of only 0.5 points on the CRI, we'll pay for that gain with a lower level of confidence. How low? Well, you can figure it out if you wish, but the confidence level would sink to about 25%. The problem is, I don't think the news organizations that paid for the poll would be very impressed when you tell them your numbers are likely to be wrong 75% of the time! We're probably not willing to pay that high a price for a narrow confidence interval.

The converse is also true: to be very very sure of yourself, you will sacrifice interval size. High levels of confidence mean a much larger confidence interval, sometimes too wide to offer any useful information. So we try to strike a balance between a reasonable level of confidence and a reasonable interval width, trading off one for the other.

Fortunately the relationship between interval width and confidence level is not a linear one. The following graph shows you what I mean:

Let's talk about what this means. Up to about a 95% level of confidence, you don't pay a whole lot in interval width to get a higher level of confidence; see how slowly the line goes up as confidence level increases? But above 95%, the cost of additional confidence is high in terms of interval width; the intervals get wider very fast as confidence level increases even a little. This shows clearly why 95% confidence is a popular level; it's close to the break point where the graph turns steep--where the cost of additional confidence may not really be worth it any more.

Data Variability: We considered this factor back at the beginning of the chapter. The more variable a population, the higher will be the standard error of the mean. Higher standard errors mean wider intervals. When we talked about this before, we agreed that there isn't much you can do about data variability, and that's fairly true. There is one thing to be done, though; and that is to use as precise a measuring instrument and measuring procedure as we can. Reducing measuring error minimizes data variability.

This relationship is linear, meaning that an increase in variability will produce the same effect on interval size, whether variability is high or low. Here's the relationship:

Sample Size: The last factor that influences interval width is sample size. We've already considered this--when we considered the effect of sample size on the standard error of the mean. Larger samples decrease the standard error, so larger samples decrease the width of the confidence interval. This relationship is nonlinear.

Here we are again, where increasing sample size pays off big in terms of a narrower interval when sample sizes are small to begin with. However, after a certain point, further increases in sample size, while they increase the work a great deal, don't pay off too well at all in narrower intervals. Once samples are really large, it takes a big increase in N to get much improvement in interval width, while we can get a big improvement in width with just a modest increase in N when the sample is small.

You may safely ignore the section in Chapter 5 called "Selecting an Appropriate Sample Size," on pages 139-140. I plan to do so.

You've finished Chapter 5. If you haven't gone through the Comprehension Checks in the chapter, I encourage you to do so. Once you've worked your way through these and checked your answers, try the Review Exercises at the end of the chapter. Remember, the answers for these are provided in your book too. This gives you many opportunities to practice and to check your understanding.

When you've finished all of the practice problems in the textbook, request a Chapter 5 worksheet via e-mail. It will be sent along with answers, so that you may check your work. When you feel ready, request the test.