Double Intergrals

7.7

Double Intergrals are when you want to take the antidervative of a function of two variables.
This is actually not that hard - if you can do anti-dervatives of functions of one variable, you can do it with two.

The Problems

There are two types of problems.

Type One

So some things to notice about this problem. First off, there are 2 of the integral signs,and both have numbers. There is also a "dx" and a "dy". You need all of these things to do the problem.

The First Intergral Sign (The one with the -1 and 1) goes with the dx (The last part) and the second intergral sign goes with the dy (The first part)

You can change this problem by rewriting it like this:

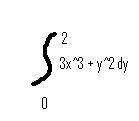
As you can see, I ignored the first intergral sign and the dx.
I kept the dy in this problem because the order went dy dx. If the order was dx dy I would keep the dx. You always keep the first one

IF you remember from partial dervatives, we treat one letter as a number and the other as a variable.
the "dy" tells us that "y" will be our variable.

So we intergrate with respect to y and get:

3x^3 *y + 1/3 y^3