| ROCKET PROPULSION |
Thrust
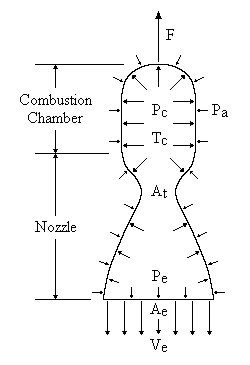
The figure to the right shows a combustion chamber with an opening, the nozzle, through which
gas can escape. The pressure distribution within the chamber is asymmetric; that is, inside the
chamber the pressure varies little, but near the nozzle it decreases somewhat. The force due to
gas pressure on the bottom of the chamber is not compensated for from the outside. The resultant
force F due to the internal and external pressure difference, the thrust, is opposite to
the direction of the gas jet. It pushes the chamber upwards.
To create high speed exhaust gases, the necessary high temperatures and pressures of
combustion are obtained by using a very energetic fuel and by having the molecular weight of the
exhaust gases as low as possible. It is also necessary to reduce the pressure of the gas as much
as possible inside the nozzle by creating a large section ratio. The section ratio, or expansion
ratio, is defined as the area of the exit Ae divided by the area of the throat At.
The thrust F is the resultant of the forces due to the pressures exerted on the inner
and outer walls by the combustion gases and the surrounding atmosphere, taking the boundary
between the inner and outer surfaces as the cross section of the exit of the nozzle. As we shall
see in the next section, applying the principle of the conservation of momentum gives
Conservation of Momentum
The linear momentum (p), or simply momentum, of a particle is the
product of its mass and its velocity. That is,
If we have a system of particles, the total momentum P of the system is the sum of
the momenta of the individual particles. When the resultant external force acting on a system
is zero, the total linear momentum of the system remains constant. This is called the principle
of conservation of linear momentum. Let's now see how this principle is applied to rocket
mechanics.
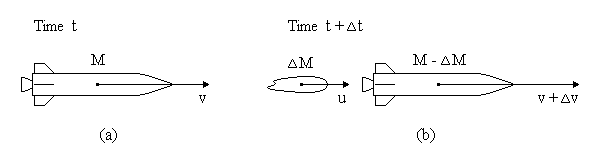
Consider a rocket drifting in gravity free space. The rocket's engine is fired for time
The figure below-left (a) shows the situation at time t. The rocket and fuel have a
total mass M and the combination is moving with velocity v as seen from a particular
frame of reference. At a time Because there are no external forces, dP/dt=0. We can write, for the time interval
In rocketry, the basic thrust equation is written as
U.S. Customary Units: In the United States, many engineers still commonly use a system in
which the base units are the units of length, force, and time. These units are respectively,
the foot (ft), the pound (lb), and the second (s). The unit of mass,
called a slug, is a derived unit and is defined as the mass which receives an
acceleration of 1 ft/s2 when a force of 1 lb is applied to it. In the study of
dynamics, where forces, masses, and accelerations are involved, we shall have to express the
mass m in slugs of a body of which the weight W has been given in pounds. That
is, m=W/g where g is the acceleration of gravity (g=32.2 ft/s2).
In the preceding section we saw that Newton's second law may be expressed in the form
When several forces act on a particle, the impulse of each of the forces must be considered.
When a problem involves a system of particles, we may add vectorially the momenta of all the
particles and the impulses of all the forces involved. When can then write
Consider a rocket of initial mass M which it launched vertically at time t=0.
The fuel is consumed at a constant rate q and is expelled at a constant speed Ve
relative to the rocket. At time t, the mass of the rocket shell and remaining fuel is
M-qt, and the velocity is v. During the time interval Integrating the above equation from t=0 to t=t gives the distance traveled by
the rocket during the burn. We obtain
The term -gt in equation (2.13) is the result of the earth's gravity pulling on the
rocket. It should be pointed out that in practice the value of g decreases with
increasing altitude, however, letting g equal the acceleration of gravity at ground level
(32.2 ft/s2 or 9.81 m/s2) yields a close approximation. Also note,
-gt is directed vertically downward. If a rocket's trajectory is at an angle other than
vertical, -gt should be replaced by -gtsin(ta), where ta is the tilt angle,
i.e. the angle between the earth's surface and the rocket's thrust vector. For a rocket drifting
in gravity-free space or in earth orbit, -gtsin(ta)=0 and can thus be omitted. Equation
(2.13) then becomes
For many spacecraft maneuvers it is necessary to calculate the duration of an engine burn
required to achieve a specific change in velocity, As stated earlier, the equations derived in this section neglect the effect of air resistance.
Drag forces can have a significant influence on a rocket moving through an atmosphere.
Isaac Newton stated in his third law of motion that "for every action there is an equal and
opposite reaction." It is upon this principle that a rocket operates. Propellants are combined
in a combustion chamber where they chemically react to form hot gases which are then accelerated
and ejected at high velocity through a nozzle, thereby imparting momentum to the engine. The
thrust force of a rocket motor is the reaction experienced by the motor structure due to
ejection of the high velocity matter. This is the same phenomenon which pushes a garden hose
backward as water flows from the nozzle, or makes a gun recoil when fired.
Thrust is the force that propels a rocket or spacecraft and is measured in pounds,
kilograms or Newtons. Physically speaking, it is the result of pressure which is exerted on the
wall of the combustion chamber.
F = q x Ve + (Pe - Pa) x Ae
where q is the rate of the ejected mass flow, Pa the pressure of the ambient
atmosphere, Pe the pressure of the exhaust gases and Ve their ejection speed.
Thrust is specified either at sea level or in a vacuum.
(2.1) p = m x v
Newton expressed his second law of motion in terms of momentum, which can be stated as "the
resultant of the forces acting on a particle is equal to the rate of change of the linear
momentum of the particle". In symbolic form this becomes
(2.2) F = dp / dt
which is equivalent to the expression F=ma.
t and, during this period, ejects gases at a constant rate and
at a constant speed relative to the rocket (exhaust velocity). Assume there are no external
forces, such as gravity or air resistance.
t later the configuration has
changed to that shown below-right (b). A mass M has been ejected
from the rocket and is moving with velocity u as seen by the observer. The rocket is
reduced to mass M-M and the velocity v of the rocket is
changed to v+v.
t
(2.3) 0 =
where P2 is the final system momentum, figure (b), and P1 is the initial system
momentum, figure (a). We write
P / t = (P2 - P1) / t
(2.4) 0 = {[(M -
If we let M) x (v + v) + (M x u)] - [M x v]} / t
t approach zero, v/t
approaches dv/dt, the acceleration of the body. The quantity M
is the mass ejected in t; this leads to a decrease in the mass
M of the original body. Since dM/dt, the change in mass of the body with time, is
negative in this case, in the limit the quantity M/t
is replaced by -dM/dt. The quantity u-(v+v) is Vrel,
the relative velocity of the ejected mass with respect to the rocket. With these changes,
equation (2.4) can be written as
M x (dv/dt) = (u - v) x (dM/dt), or
(2.5) M x (dv/dt) = Vrel x (dM/dt)
The right-hand term depends on the characteristics of the rocket and, like the left-hand term,
has the dimensions of a force. This force is called the thrust, and is the reaction force
exerted on the rocket by the mass that leaves it. The rocket designer can make the thrust as
large as possible by designing the rocket to eject mass as rapidly as possible (dM/dt
large) and with the highest possible relative speed (Vrel large).
(2.6) F = q x Ve + (Pe - Pa) x Ae
where q is the rate of the ejected mass flow, Ve is the exhaust gas ejection speed,
Pe is the pressure of the exhaust gases at the nozzle exit, Pa is the pressure of
the ambient atmosphere, and Ae is the area of the nozzle exit. The product qVe,
which we derived above (Vrel x dM/dt), is called the momentum, or velocity, thrust. The
product (Pe-Pa)Ae, called the pressure thrust, is the result of unbalanced pressure
forces at the nozzle exit. As we shall see latter, maximum thrust occurs when Pe=Pa.
Equation (2.6) then becomes F=qVe and the nozzle is said to be adapted.
International System of Units (SI units): In this system, the basic units are the units of
length, mass, and time, and are called respectively, the meter (m), the kilogram
(kg), and the second (s). The unit of force in a derived unit. It is called the
newton (N) and is defined as the force which gives an acceleration of 1 m/s2
to a mass of 1 kg.
Impulse & Momentum
F = dp/dt
Multiplying both sides by dt and integrating from a time t1 to a time t2,
we write
F x dt = dp
The integral is a vector known as the linear impulse, or simply the impulse, of
the force F during the time interval considered. The equation expresses that, when a
particle is acted upon by a force F during a given time interval, the final momentum
p2 of the particle may be obtained by adding its initial momentum p1 and the
impulse of the force F during the interval of time.
F dt = p2 - p1, or
(2.7) p1 + F dt = p2
(2.8) P1 +
For a time interval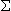 
F dt = P2
t, we may write equation (2.8) in the form
(2.9) P1 +
Let us now see how we can apply the principle of impulse and momentum to rocket mechanics.
(F x t) = P2
t,
a mass of fuel qt is expelled. Denoting by u the
absolute velocity of the expelled fuel, we apply the principle of impulse and momentum between
time t and time t+t. Please note, our derivation
neglects the effect of air resistance.
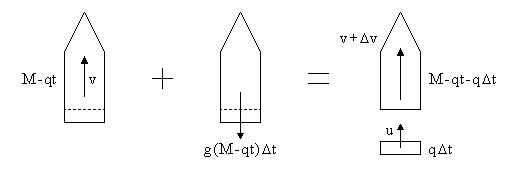
(2.10) (M - qt) x v - g x (M - qt) x
We divide through by t = (M - qt - qt) x (v + v) + qt x u
t and replace u-(v+v)
with Ve, the velocity of the expelled mass relative to the rocket. As t
approaches zero, we obtain
(2.11) -g x (M - qt) = (M - qt) x (dv/dt) - (q x Ve)
Separating variables and integrating from t=0, v=0 to t=t, v=v, we obtain
(2.12)
which equals
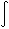dv = 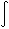[(q x Ve) / (M - qt) - g ] dt
(2.13) v = Ve x LOG[ M / (M - qt) ] - g x t
(2.14) d = Ve x { t + t x LOG[ M / (M - qt) ] + M x LOG[ (M - qt) / M ] / q } - g x t2 / 2
(2.15) v = Ve x LOG[ M / (M - qt) ]
v.
Rearranging variables in the preceding equation yields
(2.16) t = M x [ 1 - ( 1 / EXP[
V / Ve ] ) ] / q
