Analysis of the Optical Image Quality by means of Spot Diagrams
Reviewed in the October, 1997 issue of Sky & Telescope (Software Showcase p.65)
written by Ivan Krastev
The following material is a short description of computer program (SPOTDGR) that realizes analysis of optical image quality by means of spot diagrams. With this program, I wish place in the hands of amateur astronomers and telescope makers powerful tools to analyze of telescope systems. As a telescope maker, you will be able to analyze telescope systems and custom optics. This program will help you and will make you on optical expert. After you have start it, the analysis of the spot diagrams will make sense to you. SPOTDGR is a short and simple program (only 60 lines), that every telescope maker can use it for own high quality applications (for example - multi spot diagram, random spot diagram, best focus fit, aberration curves plot, optical layout, etc., see Fig.4). The basis of the program is the procedure RayTrace (line 100-280), that uses a numerical method described by Max Herzberger in his book 'Modern geometrical optics', [Ref.1]. SPOTDGR is a powerful raytracing program, that can trace unlimited number of rays through axially symmetric systems, with refracting and reflecting, flat, spherical and aspherical (parabola, hyperbola, ellipse), up to 25 optical surfaces.
CapabilitiesThe program will run on any IBM PC compatible and most work-alike. SPOTDGR runs from MS-DOS QBASIC.
Input data
The input data are as follows:
1. Number of the optical surfaces* Sk 2. Diameter of objective (entrance pupil) Diam 3. Focal length of system w 5. For each surface enter : a) radius of curvature r b) eccentricity e c) distance to the next surface d d) refractive index n * Including the focal plane. ** All dimensions in [mm].
The telescope maker must adhere strictly to the sign conventions. Before starting program, we must be sure to understand the sign conventions we will use, namely:
. Light entering the optical system travels from left to right.
. Distances from left to right are signed positive; those from right to left, negative.
. Curvatures with the convex side to the left are signed positive; otherwise, they are negative.
. The sign of the refractive index is the same as the sign of the direction in which light travels in the medium.
. In the case of reflection, therefore the signs of the refractive indices are reversed, so that n' = -n.
. Surfaces are numbered in the sequence, that they are hit by the rays.
I have chose to use the conic deformation parameter, also called the eccentricity e. The values of e are as follow:
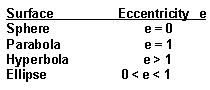
If the surface is a flat, enter e = 0 (also r = 0).
The input data appears for Newtonian and Cassegrain telescope as follows:
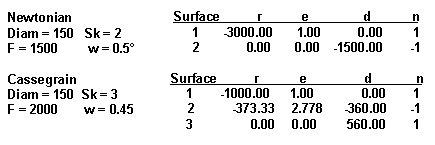
The telescope maker must enter also always as follow:
. number of surfaces plus one (the focal plane).
. for the first surface (entrance pupil); axial distance d = 0.
. for the last surface (focal plane); radius of curvature r = 0 and eccentricity e = 0.
Initialization
The initialisation parameters in program (line 40) are as follows:
dF - defocus (default dF = 0). Begin by entering the defocus dF = 0, and search for a better focal position (dF = 0) in subsequent analyses. The spot diagram will lie on this plane of defocus.
Cs - width of plotting screen (default Cs = 0.075). If we enter 0.025, the full width of the plotting screen will represent 0.025 mm. If the plotting screen width is too small (large) the analysis will have to be repeated with a larger (smaller) plotting screen.
Hi - radius vector increment (default Hi = 10).
Ti - polar angle increment (default Ti = 10).
The meaning of the last two parameters is shown in Fig.1. The lowers values of Hi and Ti determines obviously the large number of rays at the entrance pupil.
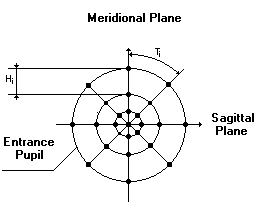
Fig.1 Regular concentric distribution of the rays at the entrance pupil.
AnalysisThe purpose of every amateur astronomer is to design telescope system, that create spot diagram with minimal diameter on focal plane, i.e. spot diagram size smaller than Airy disk for visual use (criteria for resolution by Rayleigh), and smaller than 0.025 mm (middle diameter of photographic emulsion) for photographic use.
For scale SPOTDGR shows two bars; a bar 0.025 mm long to left on the screen, and a bar equal to Airy disk diameter to right on the screen, so that quick estimate of the spot diagram is possible. The analysis of the spot diagram is possible on focal (paraxial or Gaussian) plane (dF = 0) and on plane, that lie near from the focal plane (dF <> 0).
ConclusionThe program SPOTDGR (BASIC and PASCAL source code) is stored to SpotDgr.ZIP file. Fig.2 and Fig.3 show the spot diagrams of Newtonian and Cassegrain telescope (see Input data). Fig.4 shows the power of SPOTDGR. The multi spot diagram is created with SPOTDGR that is simple modified. The last Fig.5 was created with program written with programming language PASCAL.
Download archive: SpotDgr.ZIP (10K) See also: Raytrace Applet
Reference[1] Max Herzberger, 'Modern geometrical optics', Research Laboratories 'Eastman Kodak Company', Rochester, New York, 1958, Interscince Publishers Inc.
Notice:This article was published in bulgarian astronomical magazine "Andromeda", November issue, 1999 by Astronomical Association Sofia, Bulgaria.
Please mail your comments or questions about this article to Ivan Krastev, Schulweg 3/2/3, A-2340 Moedling, AUSTRIA or send an e-mail to I.KRASTEV@KABSI.AT.
List of program SPOTDGR.BAS:1 'PROGRAM SpotDgr – written by Ivan Krastev
10 DEFSNG A-Z
20 DIM R(25), E(25), D(25), N(25), P(25), Q(25)
30 DIM X(25), Y(25), Z(25), XI(25), ETA(25), ZETA(25)
40 PI = 3.141592653#: HI = 10: TI = 10: DF = 0: CS = .075 'Initialization
50 GOTO 500
100 'PROCEDURE - Max Herzberger Ray Trace
110 X(1) = H * SIN(THETA * PI / 180): Y(1) = H * COS(THETA * PI / 180): Z(1) = 0
120 XI(1) = 0: ETA(1) = -SIN(W * PI / 180): ZETA(1) = COS(W * PI / 180)
130 P(1) = X(1) * ZETA(1): Q(1) = Y(1) * ZETA(1)
140 FOR K = 1 TO SK - 1
150 B = 1 / R(K): A = B * ((P(K) ^ 2) + (Q(K) ^ 2)): C = (ZETA(K) ^ 2)
160 DD = C + B * ((P(K) * XI(K)) + (Q(K) * ETA(K)))
170 QT = SQR((DD ^ 2) - A * B * ((N(K) ^ 2) - E(K) * (C) ^ 2))
180 Z(K) = A / (DD + QT): TT = 1 + B * Z(K) * E(K): RR = (TT ^ 2) - B * Z(K) * (TT - 1)
190 IF (N(K) / N(K + 1)) < 0 THEN QTP = -QT: PSI = -2 * QT / (RR * C): CR = CR + 1
ELSE QTP = SQR((QT ^ 2) + RR * C * ((N(K + 1) ^ 2) - (N(K) ^ 2))): PSI = (QTP - QT) / (RR * C)
200 ALPHA = PSI * (P(K) - (Z(K) * XI(K))): BETA = PSI * (Q(K) - (Z(K) * ETA(K)))
210 XI(K + 1) = XI(K) + (B * ALPHA): ETA(K + 1) = ETA(K) + (B * BETA)
220 ZETA(K + 1) = SQR((N(K + 1) ^ 2) - (XI(K + 1) ^ 2) - (ETA(K + 1) ^ 2))
230 IF (SK > 2) AND (FIX(.5 * CR) > 0) THEN ZETA(K + 1) = -ZETA(K + 1)
240 P(K + 1) = P(K) + (TT * ALPHA) - (D(K + 1) * XI(K + 1))
250 Q(K + 1) = Q(K) + (TT * BETA) - (D(K + 1) * ETA(K + 1))
260 X(K + 1) = P(K + 1) / ZETA(K + 1): Y(K + 1) = Q(K + 1) / ZETA(K + 1)
270 NEXT K
280 RETURN
500 'Main Program
510 INPUT "Number of Surfaces Sk -> ", SK
520 INPUT "Clear Diameter Diam -> ", DIAM
530 INPUT "Focal Lengt of System F -> ", F
540 INPUT "Half Field Angle w -> ", W
550 PRINT "Surface R E D N"
560 FOR K = 1 TO SK
570 LOCATE 6 + K, 3: PRINT K
580 LOCATE 6 + K, 12: INPUT "", R(K)
590 LOCATE 6 + K, 25: INPUT "", E(K)
600 LOCATE 6 + K, 35: INPUT "", D(K)
610 LOCATE 6 + K, 45: INPUT "", N(K)
620 NEXT K
630 CLS : SCREEN 2
640 RAIRY = 1.2197 * .000555 * F / DIAM
650 D(SK) = D(SK) + DF: THETA = 0: SCALE = 200 / CS
660 LINE (100, 100 - (SCALE * .0125))-(100, 100 + (SCALE * .0125))
670 LINE (540, 100 - (SCALE * RAIRY))-(540, 100 + (SCALE * RAIRY))
680 LOCATE 1, 35: PRINT "Spot Diagram": LOCATE 13, 5: PRINT "0.025 mm": LOCATE 13, 70: PRINT "Airy Size"
690 WHILE THETA <= 180
700 H = 0: GOSUB 100 'Max Herzberger Ray Trace
710 X0 = X(SK): Y0 = Y(SK): H = .5 * DIAM
720 WHILE H > 0
730 GOSUB 100 'Max Herzberger Ray Trace
740 DX = X0 - X(SK): DY = Y0 - Y(SK)
750 PSET (320 + (2 * SCALE * DX), 100 - (SCALE * DY))
760 IF THETA <> 0 AND THETA <> 180 THEN PSET (320 - (2 * SCALE * DX), 100 - (SCALE * DY))
770 H = H - HI
780 WEND
790 THETA = THETA + TI
800 WEND
810 K$ = INKEY$: IF K$ = "" THEN 810
820 SCREEN 0, 0, 0
830 END 'Main Program
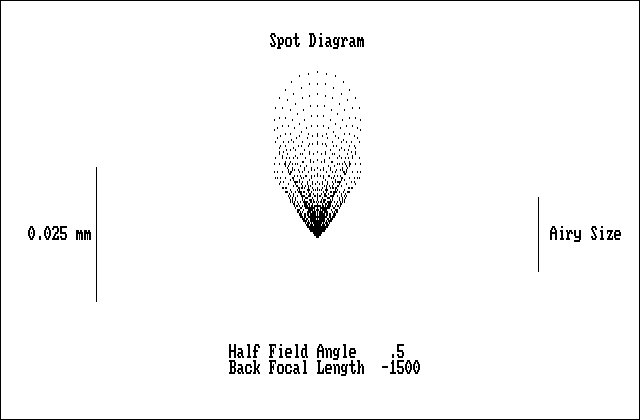
Fig.2 Spot Diagram of 150 mm Newtonian Telescope System, f/10, w = 0.5° and dF=0
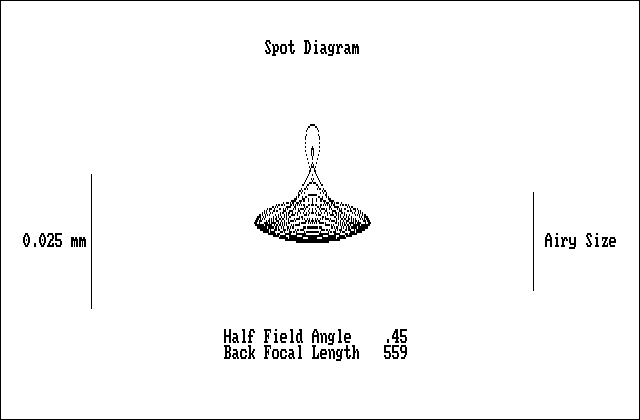
Fig.3 Spot Diagram of 150 mm Cassegrain telescope system, f/13.3, w = 0.45° and dF = -1
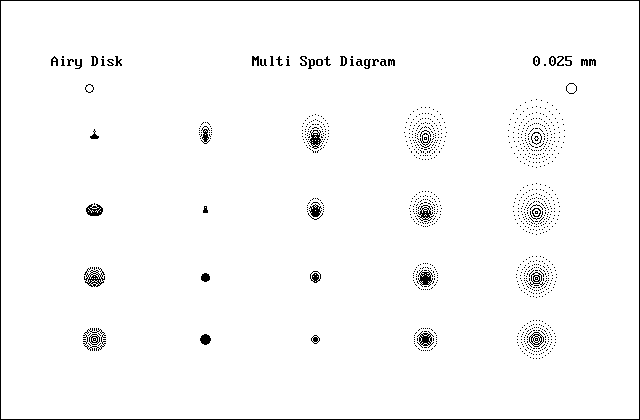
Fig.4 Multi Spot Diagram of 150 mm Cassegrain Telescope System, f/13.3 – created with modified SPOTDGR
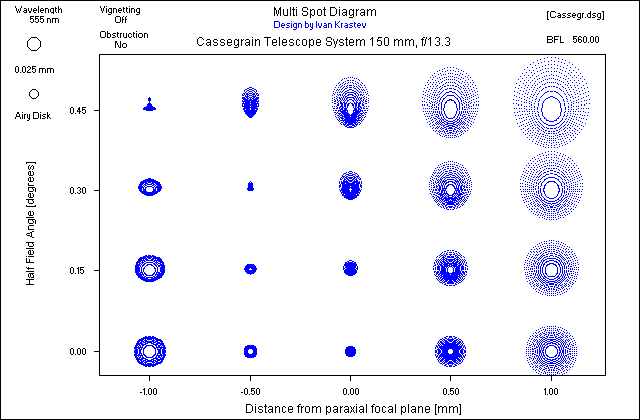
Fig.5 Multi Spot Diagram of 150 mm Cassegrain Telescope System, f/13.3 – created by SPOTDGR written with PASCAL programming language
Last Revised:
July, 2001