Due to the nature of this topic, the ostrich saga must be discontinued...now we will use the example of a soaring baseball as our projectile.
When a projectile is in motion, certain things apply to its motion. Its horizontal movement, left to right, is constant until the object is affected by an outside force like friction or air resistance, which will not be considered in the following example. The vertical movement, up and down, is constantly accelerating at -10 m/s/s. In our example, the baseball is thrown upwards at 30 m/s and to the right at 5 m/s.
The following diagram shows the path of the ball's motion through the air. This path is also commonly known as the parabola. After this diagram there will be a lot of writing and explanation because of the complicity of the topic, so enjoy!
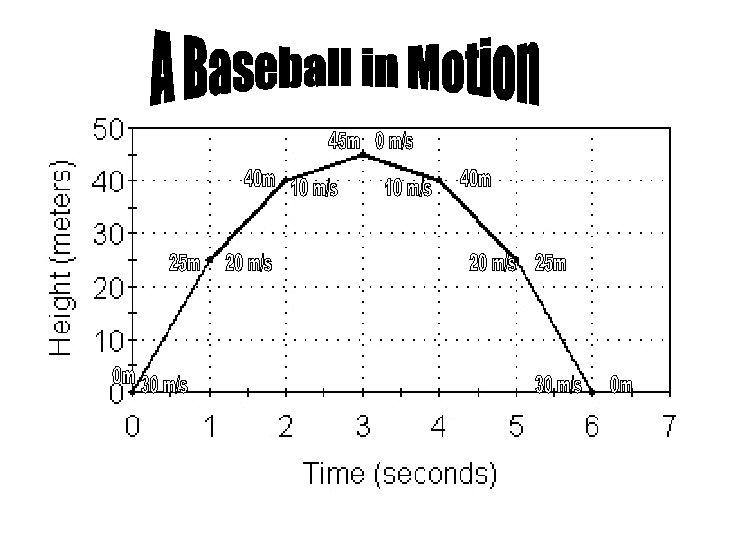
This ball was thrown up at 30 meters per second vertically, so let's focus on that velocity before continuing. The ball's speed decreases at 10 meters per second for six seconds. We get the time 6 seconds from the fact that it would take 3 seconds to reach its peak in height, and low point in speed at 0 m/s, and it would take an additional 3 seconds to arrive back on the ground, landing at 30 meters per second. Because of its consistent acceleration, the ball is at 20 meters per second after 1 second, 10 meters per second after 2 seconds, 0 meters per second after 3 seconds, -10 meters per second after 4 seconds, -20 meters per second after 5 seconds, and -30 meters per second after 6 seconds, at which point it collides with the ground some distance away from the throw. The concept of vertical velocity is best understood when a diagram such as that above is utilized. You can look at the diagram and see what the vertical velocity of the ball's motion is at each point and the effect that gravity has upon the ball during the trip. Now, let us continue onward to horizontal velocity and how far the ball would've travelled away from the launch/throw.

The horizontal velocity, when air resistance and friction is ignored, is much different than the horizontal velocity, in that there aren't any forces at work upon it other than that which launched it, or started it off. As seen in the diagram, the horizontal velocity did not change from its 5 meters per second the whole flight. This is because there is nothing working against it. This leads me to the explanation of how far the projectile, or baseball, landed away from the throw by the end of the flight. The formula for distance is a tad complicated. First, you must find the average speed of the object.
The average speed formula is the quantity of INITIAL VELOCITY + FINAL VELOCITY divided by two. In our example, the initial velocity of the first second is 30 meters per second. Add that 30 meters per second to the final velocity of 20 meters per second to get 50 meters per second. Now, divide that sum by 2 to get the average speed/velocity of the first second. The average speed for the first second is 25 meters per second. Now that we have the average speed formula, let's put it to some use.
To find out how far up the baseball went just do this:
(30 meters per second+0 meters per second)/2·3=45 meters
Well, would you look at that...with one simple formula, we were able to figure out how high up the ball went, and we didn't even have to use the diagram, even though it is a good source of reference. To find the horizontal distance, just multiply that 5 meters per second by 6 seconds. Because the velocity is unchanging, it's pretty easy to figure out. We can see that the baseball went a total of 45 meters maximum up in the air and 30 meters away from the throw. With that information alone, we are able to find out the general path of the ball. At the point where the ball was the highest, it was 15 meters away and 45 meters up. Now we have a very easily visualized parabola and path followed by the ball.

Now that that has been stated, we can figure out even more. In a parabola, we can calculate the average speed in the curve by using the equation for finding the length of the hypoteneuse of a triangle, the Pythagorean Theorem. This equation is a2+b2=c2.
Since horizontal movement is constant throughout the parabola, you can just take it once, square it, and use it over and over again as the b2value. Vertical movement always decreases by 10 meters per second, but that won't matter unless you just know a starting verticle velocity. So if the vertical velocity is 30 meters per second and the horizontal velocity is 5 meters per second, you would do 302+52 to get the value of C2. To get the value of the hypoteneuse, just find the square root of C2. In this case, the problem goes as follows:
900+25=925
The square root of 925=30.4. As a matter of reference, we will be rounding all values to the nearest tenth when necessary.
Now, direct your attention below to yet another table showing the different velocities and when they occured:
| Time (seconds) |
Velocityup (meters per second) |
Velocityside (meters per second) |
Velocity (meters per second) |
|---|---|---|---|
| 0 | 30 | 5 | 30.4 |
| 1 | 20 | 5 | 20.6 |
| 2 | 10 | 5 | 11.2 |
| 3 | 0 | 5 | 5 |
| 4 | -10 | 5 | -11.2 |
| 5 | -20 | 5 | -20.6 |
| 6 | -30 | 5 | -30.4 |
Using this table, we could recreate the diagram without using an example in front of us. With the use of the diagram and the chart, we can visualize the path of the flying ball very easily and with much celerity.

Now that we have covered the technical things, we will explain projectiles in motion...in motion.
If a cart is moving at a constant speed, and a ball is launched from it, the ball will make an arch and land at the launcher because prior to the launch, the ball had a constant speed horizontally, and when it's fired into the air, the ball will land on the same launcher that it was launched from as long as the launcher continues its previous motion from before the ball was launched. That was a bit of a mouthful, but reasonable. The vertical speed of the ball, and the length & height of the arch depends upon the force exerted by the launcher.
Now, about them angles...we won't have any exact measurements for you because there are too many to count, but we will give a general explanation of them and their pertinence to parabolas and flight paths. When an object is launched at different angles, it will go different distances. For instance, when launched directly up (90º) it will not go very far, in fact, if there isn't any horizontal velocity, the ball will not travel horizontally at all. When shot at a 0º angle, it will also not travel horizontally at all because it will immediately hit the ground. Those two angles correspond because they produce the same outcome. The angle between those two angles (45º) produces the greatest distance out of all the angles under the sun. In fact, such angles as 15º and 75º produce similar outcomes because they are an equal distance away from the 45º mark.
Well folks, that's all...to go back to the main page, click here. From there you can go anywhere else on the site.
If you wish to go to the official site for major league baseball, click here.
Thank you for visiting our site, and we hope to make another, hopefully, less complicated, website for you in the future. BYE!