Theory: As per the LCAO-MO theory, the electronic wavefunction Y_el of a molecule is assumed to be an antisymmetrised product of the occupied spin-orbitals (SOs) formed out of the occupied molecular orbitals (MOs). Here each of the MO is assumed to be a linear combination (LC) of atomic orbitals (AOs) corresponding to the constituent atoms. However, in the H₂⁺ molecular ion there is only one electron, and so here the electronic wavefunction Y_el is identical, in its spatial part, with the  lone occupied MO. This means that here the purely electronic energy E_el is same as the MO energy e of that MO.

As per the simplest MO theory of the H₂⁺ ion (also of the H₂ molecule), the two lowest-energy MOs are assumed to be linear combinations of the two 1s AOs i.e., the 1s_a & 1s_b AOs centred, respectively, on the two H nuclei a & b: thus the MO f equals (c_a 1s_a+c_b 1s_b). However, it would be grossly unrealistic to think of these contributing AOs as simply those of the contributing H-atoms: each contributing AO must have a (non-unity) orbital exponent (i.e., effective nuclear charge) k {i.e., 1s_a = k^3/2 p^–1/2 exp(–kr_a) and 1s_b = k^3/2 p^–1/2 exp(–kr_b) in atomic units} so that each generated MO f shows proper limiting behaviour as the internuclear distance R tends to zero (transforming the H₂⁺ species to He⁺ atomic ion having nuclear charge 2), or tends to infinity (separating one H-atom from an H-nuclei). Thus the exponent k must be a function of the distance R: k must equal 2 as R equals 0, must equal 1 as R equals infinity, and be somewhere in between 1 and 2 for intermediate values of R, such as the distance corresponding to the given molecular ion. 

Solving the secular equation that arises from the linear variation theory treatment for this LCAO-MO problem, we get the approximated energy e₁ of the 1st (i.e., lowest-energy) MO as e₁ = (H_aa+H_ab)/(1+S_ab). This MO itself is f = c_a(1s_a+1s_b). Here H_aa, H_ab and S_ab are defined as H_aa = ∫1s_aĤ_el1s_adv, H_ab = ∫1s_aĤ_el1s_bdv and S_ab = ∫1s_a1s_bdv, the dv = r²sinq dq.df.dr  being the volume element and Ĥ_el = –0.5+1/r_a+1/r_b (in atomic units) being the purely electronic Hamiltonian. As here the MO energy e₁ equals the purely electronic energy E_el, so we get the electronic energy U (inclusive of internuclear repulsion V_NN) is U (= E_el+V_NN) = (H_aa+H_ab)/(1+S_ab) + 1/R (here V_NN = 1/R -- in atomic units). From the form of the nuclear Schrodinger equation, we known that this energy U is also called the internuclear potential energy deciding the nuclear motions. Now, performing the three integrations defined above, it can be shown that the aforesaid integrals are expressible by the following simple relations, finally leading to values of U as a function of only R and k {noting that U = (H_aa+H_ab)/(1+S_ab) + 1/R, as mentioned above}:

Overlap integral    S_ab = (1 + k*R + k*k*R*R/3) * exp((-1)*k*R)
Coulomb integral    H_aa = 0.5*k*k - k - 1/R + (k+1/R) * exp((-2)*k*R)
Resonance Integral  H_ab = (-0.5)*k*k*Sab - k*(2-k)*(1+k*R)*exp((-1)*k*R)

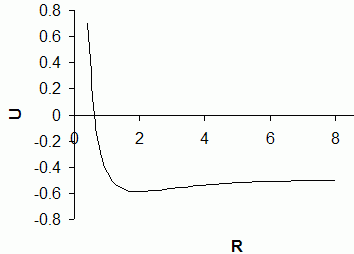
Now the value of the optimum orbital exponent k for any given distance R is obtained by again applying variation theory, this time numerically, as the value that would result in the minimum possible value of U for the given distance R. This has been done here using a small computer-program (enclosed herewith) written in Visual FoxPro 6 programming environment, in which the exponent k is varied within 1 and 2, first in steps of 0.01 and then in steps of 0.0001, and the value of k that has resulted in the minimum value of U is identified. The program then repeats this procedure for another value of the distance R. The program output displaying the (R, k) values ranging from (0.4, 1.8327) to (8, 1.0000) in steps of 0.2 atomic unit (Bohr) in R is also enclosed herewith. Using this list of (R, k) values, the values of S_ab, H_aa, H_ab and U are obtainable as functions of the internuclear distance R (using the aforementioned expressions). Now from the U vs. R plot (as shown in figure), quite realistic values for the bond-length (equilibrium internuclear distance) R_e (i.e., the value of R for which U is minimum) and for the equilibrium bond-dissociation energy D_e (the difference between U values at R = R_e and at R = a) may be obtained.

Procedure: This set of long and complicated calculation requires the use of a programmable calculator, such as the Assam-Calcu computer-software (available free of cost from many sources within the Internet). Within the Assam-Calcu command interface, one first runs the commands R = 0.4 and k = 1.8327, and then runs (after duly typing in) the above three expressions for S_ab, H_aa and H_ab one by one, and finally the aforementioned expression for U, thereby getting the value (0.7012) of U for R = 0.4. Next, one would similarly enter R = 0.6 and the corresponding appropriate (listed) value for k into Assam-Calcu, and then would just re-run the last four commands (either as recallable individual old commands, or better via the appropriate re-run command which may be generated by invoking the corresponding wizard) regarding calculation of S_ab, H_aa, H_ab and U. The new value of U (-0.0001) for R = 0.6 is thus obtained. Now one needs to repeat the above process (the same re-run command may be just recalled as an old command and used, there's no need to invoke the command-generating wizard again) for all other values of R (starting from 0.8 and up to 8.0) for which k is available within the aforesaid list. {To jot down current values of all the variables (R, k, S_ab, H_aa, H_ab, U) from one screen, the List Variables button should be clicked.} After these calculations are over, the required plot of U vs. R is to be drawn, and then the R_e and the D_e value estimated therefrom.