1. Matching The Loop Antenna

The Magnetic B Field or loop antenna is relatively inefficient as we saw in the previous analysis. The radiation resistance is small compared to the loops ohmic loss. It is therefore necessary to transfer as much energy as possible into this ohmic loss in order to maximize radiation efficiency, and through antenna reciprocity, the antenna's reception capability.

How then can we estimate the loop antenna's ohmic resistance?  The loop is essentially a single turn solenoid or "coil". It may be square, rectangular or circular, but square geometries are the most practical for fabrication, and other than this, there seems to be little reason to adopt any particular geometry over another. Printed Circuit Board (PCB) antennae are likely to be most cost effective, especially in miniature receiver or transmitter applications.

We begin with some useful formula for estimating the resistance of wires at radio frequencies and then inductance of wires in various geometries

2. DC Resistance of Copper Wire

 We begin with the published resistivity of copper

    …(1)

 so that the total resistance of a length l of copper wire with radius r becomes

…(2)                         

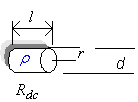
 If we consider a 40 mm length of 1 mm diameter copper wire we find that .

3. AC Resistance of Copper Wire

The resistance of a conductor tends to increase with frequency as the current flowing through it tends to crowd towards the outer surface. This sets up an exponential radial distribution in current density J given by

…(3)

where  refers to the distance from the outer surface to some internal position and  is defined as a “skin depth”, which identifies where the majority of conduction occurs. This “skin depth” coefficient d is usually predicted as

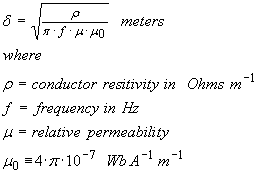            …(4)

or alternatively, since , and for copper wire where

            …(5)

If we assume that , then the skin depth  for copper wire will be . This depth will usually be far less than the wire diameter, but  does define the average depth current flows over (which can be shown by integrating equation (3). The effective area A_e of the wire can interpreted as a cylindrical segment towards the outer surface of the wire

Given this interpretation

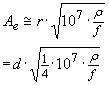…(6)

Providing f is sufficiently high so that skin depth issues dominate, the ac resistance for a length l of wire with diameter d = 2 r will be

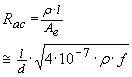  …(7)

Using the previous example 40 mm length of 1mm diameter copper wire with a DC resistance of 852 we find that this increases to  at a frequency of 150 MHz, i.e. almost 50 times higher at VHF!

4. Inductance of Magnetic Loop Antenna

We will now estimate the inductance of several loop geometries,

4.1. Inductance of straight round wire

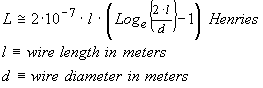
In this example, 40 mm of 1 mm diameter copper wire will have an inductance of 21.51 nH.

4.2. Inductance of Square Loop

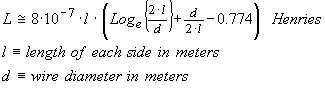
Let us now imagine this 40 mm length of 1 mm diameter wire bent into a square shape so that  in this equation. The new inductance will be 18.17 nH. A slight reduction has occurred, presumably because opposing side segments have magnetic fields in opposition.

4.3. Inductance Of Circular Loop

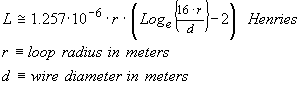
Now let’s imagine the same length of wire bent into a circle. In order to retain a circumference of 40 mm its radius will need to be 6.366 mm. The predicted inductance will therefore be 20.99 nH. We note that this is slightly higher than the square loop, as each opposing magnetic side segment is maximally distant from each other. The total inductance is still less than the original straight wire example.  

5. Impedance Of Square Loop Antenna

 We will concentrate on square loop antennae, as these are usually easier to fabricate than circular versions. We recall that

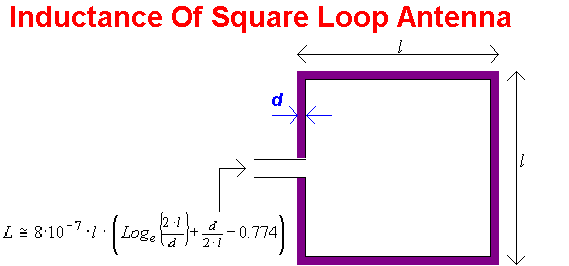
 The inductive reactance component of the loop will therefore be

…(11)

 Again, a square with a side segment length of 10 mm made from 1 mm diameter copper wire will have an inductive reactance of 17.13 Ohms at f = 150 MHz.

We recall from equation (7) that   where l represented the total wire length, so that the modified expression with l representing the side segment length must be,

…(12)

The ac resistance at f = 150 MHz will be 40.08 , which will be in series with the radiation loss component . From the previous chapter this was predicted to be  where  represents the fractional length of one side compared to a wavelength. The radiation resistance at a given frequency is therefore

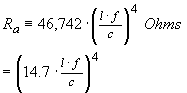            …(13)

Continuing with the example, the radiation resistance of a 10 mm square loop will be 29.2  at f = 150 MHz. This is significantly less than the ohmic loss, as would be expected for an electrically small loop antenna.

The equivalent loop antenna reactance will therefore be

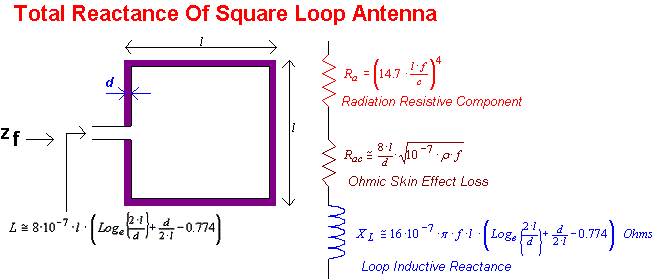
The maximum achievable “Q” of the loop can be defined as the inductive reactance divided by the ohmic losses associated with its conductor,

Recalling the ohmic loss resulting from the skin effect mechanism

…(14)

And the loop inductive reactance

…(15)

We predict the maximum achievable Q of the loop to be

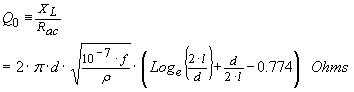…(16)

This suggests that the maximum achievable Q for a small square loop antenna with 10 mm side segments made from 1 mm wire to be 408.6. In practice, other losses will be dominant, such as dielectric loss and effective series resistance associated with resonating capacitors. A more practical total Q prediction will be in the order of 200 ~ 300.

Return to Magnetic B Field Antenna

or Kaleidoscope Comms