![]() Questão: Determine, diretamente por integração a posição do centróide da superfície
hachurada na Figura 1. Adote
Questão: Determine, diretamente por integração a posição do centróide da superfície
hachurada na Figura 1. Adote
![]() e
e

![]() Questão: Determine, diretamente por integração o momento de inércia em relação ao eixo
Questão: Determine, diretamente por integração o momento de inércia em relação ao eixo
![]() para a superfície
hachurada na Figura 1. Adote
para a superfície
hachurada na Figura 1. Adote
![]() e
e

![]() Questão: O carretel apresentado na Figura 2 foi gerado a partir do giro do trapézio FGHI em
torno do eixo AB. O sólido é constituído de material homogêneo cuja massa específica é igual a
Questão: O carretel apresentado na Figura 2 foi gerado a partir do giro do trapézio FGHI em
torno do eixo AB. O sólido é constituído de material homogêneo cuja massa específica é igual a
![]() .
Admitindo que y=4cm, w=2cm, a = 0,5 b = c = 2cm e
.
Admitindo que y=4cm, w=2cm, a = 0,5 b = c = 2cm e
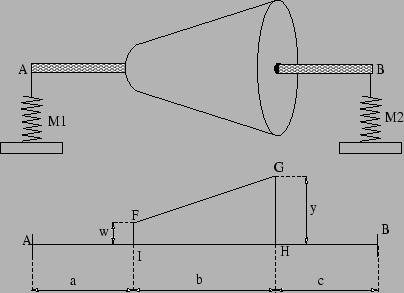 , determine as reações nos apoios A e B.
Determine também a relação linear entre as constantes elásticas das molas M1 e M2 para que as ordenadas
dos pontos A e B sejam iguais, ou seja, para que o eixo AB permaneça na horizontal.
, determine as reações nos apoios A e B.
Determine também a relação linear entre as constantes elásticas das molas M1 e M2 para que as ordenadas
dos pontos A e B sejam iguais, ou seja, para que o eixo AB permaneça na horizontal.
![]() : Sabendo que
: Sabendo que
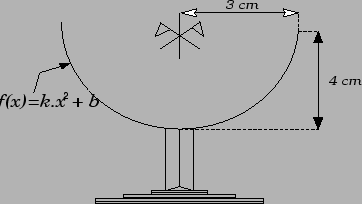 determine quantos mililitros cabem na taça cuja seção
transversal está apresentada na figura abaixo.
determine quantos mililitros cabem na taça cuja seção
transversal está apresentada na figura abaixo.
![]() Questão:Preencha corretamente a tabela abaixo, informando as medidas de inércia das figuras
indicadas na coluna da esquerda. Admita
Questão:Preencha corretamente a tabela abaixo, informando as medidas de inércia das figuras
indicadas na coluna da esquerda. Admita
![]() e
e
 . Admita que as seções da penúltima e da
última linha são construídas a partir da soldagem do perfil C, indicado na tabela. Assuma que
. Admita que as seções da penúltima e da
última linha são construídas a partir da soldagem do perfil C, indicado na tabela. Assuma que
![]() e
e
 são respectivamente paralelos aos eixos
são respectivamente paralelos aos eixos
![]() e
e
![]() indicados nas figuras e passam pelos
centróides das seções. Após preenchida a tabela indique, justificando sua indicação, qual dos três perfis
oferece maior resistência a rotação em torno do eixo cartesiano
indicados nas figuras e passam pelos
centróides das seções. Após preenchida a tabela indique, justificando sua indicação, qual dos três perfis
oferece maior resistência a rotação em torno do eixo cartesiano
![]()
![]() Questão: Um reservatório cilíndrico é sustentado por três barras conectadas a um pilar central conforme
mostra a Figura 8.4. Determine o valor das forças compressivas nas barras que ligam o reservatório ao
pilar central, considerando apenas o peso da água, nas seguintes situações: a) Reservatório com 25 % de sua capacidade,
b) Reservatório com 75 % de sua capacidade e finalmente, c) Reservatório com 100 % de sua capacidade. Admita:
1-Massa específica da água =
Questão: Um reservatório cilíndrico é sustentado por três barras conectadas a um pilar central conforme
mostra a Figura 8.4. Determine o valor das forças compressivas nas barras que ligam o reservatório ao
pilar central, considerando apenas o peso da água, nas seguintes situações: a) Reservatório com 25 % de sua capacidade,
b) Reservatório com 75 % de sua capacidade e finalmente, c) Reservatório com 100 % de sua capacidade. Admita:
1-Massa específica da água =
![]() ; 2-Aceleração da gravidade = 10
; 2-Aceleração da gravidade = 10
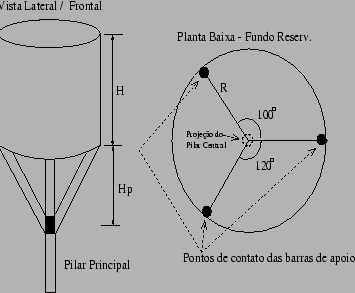 ; 3- Raio da base do reservatório =
2,5 metros ; 4- H = 5 metros e finalmente 5- Hp = 3 metros
; 3- Raio da base do reservatório =
2,5 metros ; 4- H = 5 metros e finalmente 5- Hp = 3 metros