Chapter One

The Basics

Lines:
	Slope: m = rise/run = @y/@x = (Y2-Y1)/(X2-X1)
		Explanation: The general equation for finding the slope of a line.
	
	Point-slope: y-y1 = m(x-x1)
		Explanation: Used to find the slope of a line when only a point it goes 
			     through is given.
	
	Slope-intercept: y = mx + b
		Explanation: Gives you the slope of a line with y-intercept at b.


Functions:
	Function: a rule which assigns to each element x in the domain, a single element 
		  y in the range.

	Domain: the domain of a function f is the set of all real numbers for which f is 
		defined. 

	Range: the range of a function is all of the y values that result from the input 
	       of the domain.

	Even functions: 
		An even function is a function which has symmetry about the y-axis.  
			f(-x) = f(x)

	Odd Functions:
		An odd function is a function which has symmetry about the origin. 
			f(-x) = -f(x)

	Exponential functions:
		An exponential function is f(x) = ax, where a = a positive real number 
		other than 1.


Rules for Exponents:
	1.  ax • ay = ax+y
	2.  ax / ay = ax-y
	3.  (ax)y = (ay)x = axy
	4.  ax • bx = (ab)x
	5.  (a/b)x = ax/bx

	Exponential Growth / Decay:
		Exponential growth can be described with the equation y = k • ax, when k > 1 and a >1.
		Exponential Decay uses the same equation, but  0 < a < 1.  


Functions and Logarithms:
	One-to-One function: A type of function that assigns a different element in the 
	range to each element in the domain so that no two domain elements map to the 
	same range element.  Tested with horizontal line test.


Logarithms:
	Base a logarithms are represented by the equation y = logax, which is the inverse 
	of the base a exponential function y = ax (a>0, a --? 1).
	
	Other logarithms:
		logxx = ln x
		log10x = log x


Properties of Logarithms:
	Inverse Properties:
		Base a: alogax = x, logaax = x, a > 1, x > 0
		Base e: elnx = x, ln ex = x, x > 0

	Other Properties:
		Product rule:  logaxy = logax + logxy
		Quotient Rule:  logax/y = logax – logay
		Power Rule: logaxy = y logax

	Change of Base Formula:
		logxx = ln x / ln a 

***NOTE: This can be used to evaluate a base a logarithm function on your calculator.


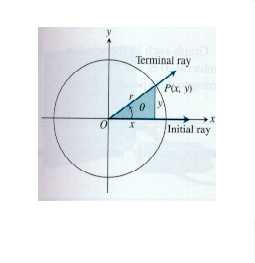
Trigonometric Functions:
	Sine:  sin q = y/r	
	Cosine: cos q = x/r
	Tangent: tan q = y/x
	Cosecant: csc q = r/y
	Secant: sec q = r/x
	Cotangent: cot q = x/y

     


Periodic / Period:
	A function is periodic if there is a positive number h so that there is a point 
	or points where f(x+h) = f(x).  The smallest of these is the function’s period.  


Transformations of Trigonometric Graphs:
	Like all other functions, trigonometric functions can also be even or odd.  

	This is a model to explain all of the transformations possible for a trigonometric 
	function:  
		y = a f(b(x+c)) + d
			a = vertical stretch or shrink; reflection about the x-axis.
			b = Horizontal stretch or shrink; reflection about y-axis.
			c = horizontal shift
			d = vertical shift


Inverse Trigonometric Functions:
 	 Function	    Domain	         Range        .
	y = sin-1x	  -1 ≤ x ≤ 1	    0 ≤ y ≤ π
	y = cos-1x	  -1 ≤ x ≤ 1	    - π /2 ≤ y ≤ π /2
	y = tan-1x	  - ∞ < x < ∞   - π /2 < y < π /2          
	y = sec-1x	  |x| ≥ 1	    0 ≤ y ≤ π , y ¹ π /2
	y = csc-1x	  |x| ≥ 1	    - π /2 ≤ y ≤ π /2, y ¹ 0
	y = cot-1x	  - ∞ < x< ∞	    0 < y < π