|
Torque and Rotational Inertia
Introduction
According to Newton's Second Law for linear
quantities
F = ma
Relating angular acceleration to tangential linear
acceleration
aT = r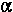
If we combine the two
equations
F = mr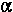
If we multiply both sides of the equation by
r
Fr = 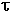 = mr2 = mr2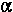 For a Single Particle
For a Single Particle
mr2 represents the rotational inertia of the particle and is called
the moment of inertia.
For rigid bodies that has many particles at different distance from the axis of
rotation 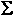 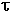 = (
= (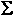 mr2) mr2) 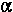
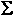 mr2 is the
Moment of Rotational Inertia of the object and has the symbol I. There is
a chart for different shape objects at the bottom of this page. Moments of Inertia mr2 is the
Moment of Rotational Inertia of the object and has the symbol I. There is
a chart for different shape objects at the bottom of this page. Moments of Inertia
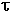 = I
= I
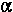
I can also be calculated using the radius of gyration,
k. It is an average radius.
I = MK2
Table of Contents
Problems
| 1. |
An oxygen molecule consist of two oxygen
atoms whose total mass is 32 amu and whose moment of inertia about an axis
perpendicular to the line joining the two atoms, midway between them, is
1.9 x 10 -46 kg . m2. Estimate the
effective distance between the atoms. Moments of Inertia
|
| 2. |
In order to get a uniform spherical
satellite spinning at the correct rate, engineers fire four tangential
rockets that are equally spaced around the cylinder and creating torque in
the same direction. If the satellite has a mass of 2500. kg and
a radius of 3.50 m, what is the required constant force for each
rocket to achieve 45.0 rpm in 4.00 minutes? Moments of Inertia
|
| 3. |
A grinding wheel is a uniform cylinder with
a radius of 8.25 cm and a mass of 750. g. Calculate (a) its
moment of inertia about its center, and (b) the applied torque needed to
accelerate it from rest to 2500. rpm in 9.50 s if it is known to
slow down from 1250 rpm to rest in exactly 1 minute. Moments of Inertia
|
| 4. |
A softball player swings a bat, accelerating
it from rest to 4.25 rev/s in 0.25 s. Approximate the bat as a
2.5 kg uniform rod of length 89 cm, and compute the torque the player
applies to one end of the bat. Moments of Inertia
|
| 5. |
A small 1.33 kg ball on the end of an
extremely light rod is rotated in a horizontal circle of radium 85.5
cm. Calculate (a) the moment of inertia of the system about the
axis of rotation, and (b) the torque needed to keep the ball rotating at
constant angular velocity if air resistance exerts a force of 0.0750 N on
the ball. Moments of Inertia
|
| 6. |
A day-care worker pushes tangentially on a
small hand-driven merry-go-round and is able to accelerate it from rest to
a spinning rate of 35.0 rpm in 10.0 s. Assume the
merry-go-round is a disk of radius 2.25 m and has a mass of
750. kg. Two children, 30.0 kg each, sit opposite each other on
the edge. Calculate the torque required to produce the acceleration,
ignoring friction. What force is required? Moments of Inertia |
Table of Contents
Answers
| 1. |
An oxygen molecule consist of two oxygen
atoms whose total mass is 32 amu and whose moment of inertia about an axis
perpendicular to the line joining the two atoms, midway between them, is
1.9 x 10 -46 kg . m2. Estimate the
effective distance between the atoms. Moments of Inertia
|
|
1 kg
32 amu x -------------------------- = 5.3 x 10 -26 kg
6.02 x 10 26 amu
This is a two body system where
 = (
= ( mr2) mr2) = (m r2 + mr2)
= (m r2 + mr2) = 2mr2
= 2mr2 = I = I Solve for r.
Solve for r.
I
1.9 x 10 -46 kg . m2
r = ( ---- ) 1/2
= ( ------------------------- ) 1/2 =
6.0 x 10 -11 m
2m
5.3 x 10 -26 kg
Distance between molecules = 2r = 2 x 6.0 x 10
-11 m = 1.2 x 10 -10 m
|
|
|
| 2. |
In order to get a uniform spherical
satellite spinning at the correct rate, engineers fire four tangential
rockets that are equally spaced around the cylinder and creating torque in
the same direction. If the satellite has a mass of 2500. kg and
a radius of 3.50 m, what is the required constant force for each
rocket to achieve 45.0 rpm in 4.00 minutes? Moments of Inertia
|
|
45.0
rev 1
min 2 r r
------------ x --------- x ---------- = 4.71 rad s
-1
1
min 60
s 1 rev
/\ 4.71 rad s -1 - 0 rad s -1
4.71 rad s -1 - 0 rad s -1
 = ---------- = -----------------------------------
= 0.0196 rad s -2
= ---------- = -----------------------------------
= 0.0196 rad s -2
/\t
240. s
Total Force = 4 x force for 1 rocket = 4F
 =
r =
r = I = I = 4rF
= 4rF
I = 2/5 mR2
From Moments of Inertia
Chart
2/5 m R2  =
4rF
Solve for F.
=
4rF
Solve for F.
mr 2500. kg x 3.50 m x 0.0196 rad s -2
2500. kg x 3.50 m x 0.0196 rad s -2
F = ------------- =
------------------------------------------------ = 17.2 N
10
10
|
|
|
| 3. |
A grinding wheel is a uniform cylinder with
a radius of 8.25 cm and a mass of 750. g. Calculate (a) its
moment of inertia about its center, and (b) the applied torque needed to
accelerate it from rest to 2500. rpm in 9.50 s if it is known to
slow down from 1250 rpm to rest in exactly 1 minute. Moments of Inertia
|
|
(a) I =  mR2
From Moments of Inertia
Chart
mR2
From Moments of Inertia
Chart
I =  x 0.750 kg x ( 0.0825 m ) 2 = 0.00255 kg m 2
x 0.750 kg x ( 0.0825 m ) 2 = 0.00255 kg m 2
(b)
2500
rev 1
min 2 r r
------------- x --------- x ---------- = 262 rad s
-1
1
min
60 s 1 rev
1250
rev 1
min 2 r r
------------- x --------- x ---------- = 131 rad s
-1
1
min
60 s 1 rev
/\ 0 rad s -1 - 131 rad s -1
0 rad s -1 - 131 rad s -1
 fr
= ---------- = -----------------------------------
= - 2.18 rad s -2 fr
= ---------- = -----------------------------------
= - 2.18 rad s -2
/\t
60. s
/\ 262 rad s -1 - 0 rad s -1
262 rad s -1 - 0 rad s -1
 = ---------- = -----------------------------------
= 27.6 rad s -2
= ---------- = -----------------------------------
= 27.6 rad s -2
/\t
9.50 s
Sufficient torque must be applied to overcome
friction in addition to accomplish the desired accelertion.
 Total
= 27.6 rad s -2 + 2.18 rad s -2
= 29.8 rad s -2 Total
= 27.6 rad s -2 + 2.18 rad s -2
= 29.8 rad s -2
 =
I =
I = 0.00255
kg m 2 x 29.8 rad s -2 =
0.0760 m . N = 0.00255
kg m 2 x 29.8 rad s -2 =
0.0760 m . N
|
|
|
| 4. |
A softball player swings a bat, accelerating
it from rest to 4.25 rev/s in 0.25 s. Approximate the bat as a
2.5 kg uniform rod of length 89 cm, and compute the torque the player
applies to one end of the bat. Moments of Inertia
|
|
I = 1/3 mL2 = 1/3 x 2.5 kg
x 0.89 m = 0.74 kg m 2
From Moments of Inertia
Chart
4.25
rev 2 r r
------------ x --------- = 26.7 rad
s -2
1
s
1 rev
/\ 26.7 rad s -1 - 0 rad s -1
26.7 rad s -1 - 0 rad s -1
 = ---------- = -----------------------------------
= 110 rad s -2
= ---------- = -----------------------------------
= 110 rad s -2
/\t
0.25 s
 = I
= I = 0.74 kg m 2 x
110 rad s -2 = 81 m . N
= 0.74 kg m 2 x
110 rad s -2 = 81 m . N
|
|
|
| 5. |
A small 1.33 kg ball on the end of an
extremely light rod is rotated in a horizontal circle of radium 85.5
cm. Calculate (a) the moment of inertia of the system about the
axis of rotation, and (b) the torque needed to keep the ball rotating at
constant angular velocity if air resistance exerts a force of 0.0750 N on
the ball. Moments of Inertia
|
|
(a) I = mr2
= 1.33 kg x ( 0.855 m )2 = 0.972 kg m 2
Moment of Inertia of a single point.
(b)  = r
= r = 0.855 m x 0.0750 N = 0.0641 m
. N
= 0.855 m x 0.0750 N = 0.0641 m
. N
|
|
|
| 6. |
A day-care worker pushes tangentially on a
small hand-driven merry-go-round and is able to accelerate it from rest to
a spinning rate of 35.0 rpm in 10.0 s. Assume the
merry-go-round is a disk of radius 2.25 m and has a mass of
750. kg. Two children, 30.0 kg each, sit opposite each other on
the edge. Calculate the torque required to produce the acceleration,
ignoring friction. What force is required? Moments of Inertia
|
|
35.0
rev 1
min 2 r r
----------- x --------- x ---------- = 3.67
rad s -1
1
min 60
s 1 rev
/\ 3.67 rad s -1 - 0 rad s -1
3.67 rad s -1 - 0 rad s -1
 = ---------- = -----------------------------------
= 0.367 rad s -2
= ---------- = -----------------------------------
= 0.367 rad s -2
/\t
10.0 s
I =  mcylinderR2 + mchildrenR2
=
mcylinderR2 + mchildrenR2
=  x 750. kg x ( 2.25 m
)2 + 60.0 kg x ( 2.25 m )2 =
2.20 x 10 3 kg m2 x 750. kg x ( 2.25 m
)2 + 60.0 kg x ( 2.25 m )2 =
2.20 x 10 3 kg m2
 = I
= I = 2.20 x 10 3
kg m 2 x 0.367 rad s -2 =
807 m . N
= 2.20 x 10 3
kg m 2 x 0.367 rad s -2 =
807 m . N
 =
r =
r Solve for perpendicular force.
Solve for perpendicular force.
 807 m . N
807 m . N
 =
---- = --------------- = 359 N =
---- = --------------- = 359 N
r 2.25 m
|
Table of Contents
Moments of
Inertia
| Object |
Location
of Axis |
|
Moment
of Inertia |
Radius of
Gyration |
| Thin Loop of radius, R |
Through
Center |
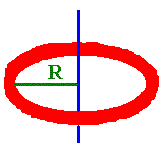 |
MR2 |
R |
| Uniform cylinder of radius, R |
Through
Center |
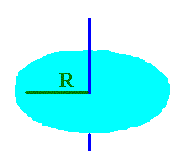 |
1/2 MR2 |
R
----
2 1/2 |
| Uniform sphere of radius, R |
Through
Center |
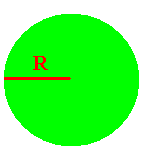 |
2/5 MR2 |
2
( -- )1/2 R
5 |
| Long uniform rod of length, L |
Through
Center |
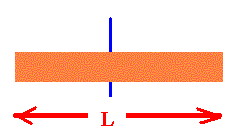 |
1/12 ML2 |
L
---------
12 1/2 |
| Long uniform rod of length, L |
Through
End |
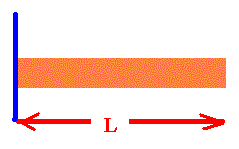 |
1/3 ML2 |
L
----------
3 1/2 |
Table of Contents
|