|
Intensity of Sound
Introduction
The loudness of a sound is related to the sounds
intensity. The intensity is measured in watt/meter2 and is
proportional to the square of the wave amplitude.
| Threshold of Hearing |
The lowest intensity of sound detected by
the human ear. It varies both with individuals and the frequency of
sound. I = 10 -12 W/m2.
|
| Threshold of Pain |
When the intensity of sound gets too great,
it creates pain in the human ear. It varies with frequency. I
= 1 W/m2. Humans still detect sound above the threshold
of pain.
|
Human ears have the ability to detect sound over an extremely
large range and some animals have an even greater range. It ranges from
the threshold of hearing, 10 -12 W/m2 to over the
threshold of pain, 1 W/m2. This is a range of over 1000
billion.
To produce a sound that is perceived as twice as loud, the
intensity must be 10 times greater.
The intensity level, 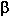 ,
is defined relative to the threshold of hearing. We commonly use dB
because the bel is too small a unit. ,
is defined relative to the threshold of hearing. We commonly use dB
because the bel is too small a unit.
I
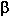 (measured in dB) = 10 log ---- (measured in dB) = 10 log ----
Io
The table below includes the Intensity Level of common
sounds.
Intensity
of Various Sounds
|
| Source of the Sound |
Intensity Level (dB) |
Intensity (W/m2) |
| Jet plane at 30 m |
140 |
100 |
| Threshold of pain |
120 |
1 |
| Loud indoor rock concert |
120 |
1 |
| Siren at 30 m |
100 |
1 x 10 -2 |
| Auto interior, moving at 90 km/h |
75 |
3 x 10 -5 |
| Busy street traffic |
70 |
1 x 10 -5 |
| Ordinary conversation at 50 cm |
65 |
3 x 10 -6 |
| Quiet radio |
40 |
1 x 10 -8 |
| Whisper |
20 |
1 x 10 -10 |
| Rustle of leaves |
10 |
1 x 10 -11 |
| Threshold of hearing |
0 |
1 x 10 -12 |
Table of Contents
Problems
| 1. |
A stereo tape recorder has a signal to noise
ratio of 58 dB. What is the ratio of intensities of two sounds whose
levels differ by this amount?
|
| 2. |
Steve standing 30. m from an airplane with
four equally noisy engines feels an intensity level of 120. dB. If
the pilot cuts off all except one engine, what intensity level does Steve
now detect?
|
| 3. |
Calculate the power output of Ashley's mouth
in a normal conversation. Assume the sound leaves her mouth in a
uniform hemispherical shape. How many of her classmates, are
necessary to create 100. W?
|
| 4. |
Jessica's Father measures a sound intensity
level of 90. dB between 9 PM and 10 PM when she is playing her
stereo. She turns off her stereo at 10 PM, but Jennifer turns on her
stereo between 10 PM and 11 PM, and her Father measures
100. dB. At 11 PM, Jessica turns her stereo up to its original
level. What sound intensity does their Father now measure? |
Table of Contents
Answers
| 1. |
A stereo tape recorder has a signal to noise
ratio of 58 dB. What is the ratio of intensities of two sounds whose
levels differ by this amount?
|
|
I
 = 10 log ---- = 10 log ----
Io
I
10 B/10 = ---- =>
I = Io x 10 B/10
Io
Ihigh
Io x 10 B high/10
10 B high/10
-------- = ---------------------- =
-------------------
Ilow
Io x 10 B low/10
10 B low/10
Ihigh
10 58/10
-------- = --------------- = 5.0 x 10 5
Ilow
10 1/10
|
|
Definition of sound levels.
To get rid of log term, you must take
the antilog of both sides. First get all nonlog terms on the
same side.
antilog X = 10 X
Set up a ratio of Intensities.
To have a noise ratio of 58 dB
B high = 58 dB and B
low = 1 dB |
|
|
|
| 2. |
Steve standing 30. m from an airplane with
four equally noisy engines feels an intensity level of 120. dB. If
the pilot cuts off all except one engine, what intensity level does Steve
now detect?
|
|
I
 = 10 log ----
= 10 log ----
Io
I
10 B/10 = ---- =>
I = Io x 10 B/10
Io
I = 1
x 10 -12 W/m2 x 10 120/10
= 1 W/m2
I new = 1 W/m2
/ 4 = 0.25 W/m2
I
0.25 W/m2
 = 10 log ---- = 10 log ----------------------- = 114 dB
= 10 log ---- = 10 log ----------------------- = 114 dB
Io
1 x 10 -12 W/m2
|
|
Start with the definition of sound
intensity.
Solve for Intensity.
Divide the intensity by 4 since only 1
engine is still running.
Calculate the new sound level. |
|
|
|
| 3. |
Calculate the power output of Ashley's mouth
in a normal conversation. Assume the sound leaves her mouth in a
uniform hemispherical shape. How many of her classmates, are
necessary to create 100. W?
|
|
I
 = 10 log ----
= 10 log ----
Io
I
10 B/10 = ---- =>
I = Io x 10 B/10
Io
I = 1 x 10 -12 W/m2
x 10 65/10 = 3.2 x 10 -6 W/m2
P = IA = 3.2 x 10 -6
W/m2 x 2 x (0.50
m)2 = 5.0 x 10 -6 W x (0.50
m)2 = 5.0 x 10 -6 W
1 person
-------------------- x 100 W = 2.0 x 10 7 people
5.0 x 10 -6 W
|
|
Intensity level equation.
Solve equation for intensity.
P = IA (check out units)
Area of a sphere = 4 r2 r2
Hemisphere would have 1/2 this area.
Power rating was for just Ashley.
|
|
|
|
| 4. |
Jessica's Father measures a sound intensity
level of 90. dB between 9 PM and 10 PM when she is playing her
stereo. She turns off her stereo at 10 PM, but Jennifer turns on her
stereo between 10 PM and 11 PM, and her Father measures
100. dB. At 11 PM, Jessica turns her stereo up to its original
level. What sound intensity does their Father now measure?
|
|
I
 = 10 log ----
= 10 log ----
Io
I
10 B/10 = ---- =>
I = Io x 10 B/10
Io
I = 1.0 x 10 -12 W/m2
x 10 90/10 = 1.0 x 10 -3 W/m2
I = 1.0 x 10
-12 W/m2 x 10 95/10 = 3.2 x
10 -3 W/m2
I total = 1.0 x 10
-3 W/m2 + 3.2 x 10 -3 W/m2
= 4.2 x 10 -3 W/m2
I
4.2 x 10 -3 W/m2
 = 10 log ---- = 10 x log -------------------------- = 96
dB
= 10 log ---- = 10 x log -------------------------- = 96
dB
Io
1.0 x 10 -12 W/m2
|
|
Intensity level equation.
Solve equation for intensity.
Calculate intensity of both stereo's.
Add intensities to get total intensity.
Calculate new intensity level. |
|
Table of Contents
|