|
Simple Harmonic Motion
Vibration or
Oscillation |
The motion of an object that regularly
repeats itself, back and forth, over the same path. Simplest form is
represented by an object oscillating on the end of a coil spring.
This motion is periodic.
|
| Equilibrium position |
The position when no external force is on
the mass.
|
| Amplitude |
The greatest displacement from the
equilibrium position.
|
| Frequency |
The number of complete cycles per
second. The mass moves from its original position and returns
to the same position with the same motion. A complete cycle is shown
below. Changing from step (b) to step (d) is not a cycle.
Although the mass is in the same position, it is moving inward in step (b)
and outward in step (d).
|
| Period |
The time required for one complete
cycle. |
1
1
f = --- = frequency and T = ---
= period
T
f
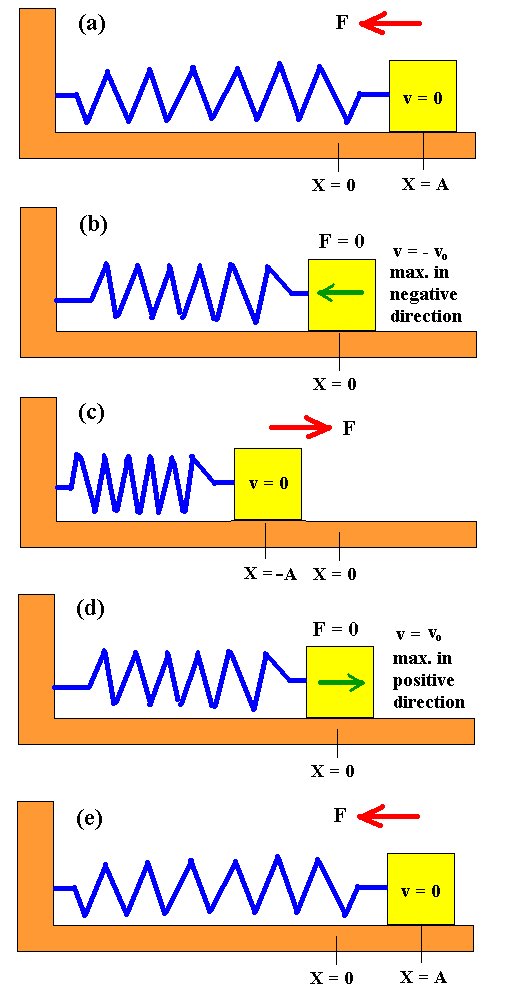
The diagram to the left illustrates the forces, displacement,
and velocities at various positions in a cycle.
In step (a), the spring has been stretched and released.
This is the instant the mass has been released. The maximum force is on
the object pulling the object inward. The object has not started moving
and it is at its maximum displacement.
In step (b), the mass has reached its equilibrium
position. There is no force on the object and it is at the maximum
velocity in the negative direction.
In step (c), the spring has reached its maximum
compression. The mass has stopped moving and reached its maximum
displacement. The force is at its maximum and is pushing the mass outward.
In step (d), the mass has reached its equilibrium
position. There is no force on the object and it is at the maximum
velocity in the positive direction.
The mass has returned to its original position.
| Simple Harmonic Motion |
The vibrating system has a restoring force
that is directly proportional to the negative of the
displacement. F = - kx
|
| Simple Harmonic Oscillator |
A system that has simple harmonic motion. |
|