"Sync or sink " (Third law of synthesis).
 

As everyone knows, good recording techniques dictates that, in an ideal configuration, no more than one microphone output should be recorded into a tape track at a time.

Why? Because phase relationships are extremely important when mixing sounds together : when two signals of identical frequency but unequal amplitude are out of phase, their summation will cause a partial cancellation of the mixed signals. Also, when two signals are of identical amplitude and 180 degrees out of phase, their summation will result in complete cancellations of the two sounds.

This fact is well known to professional TV broadcasters and recording artists. Indeed, whenever possible, audio phases should be monitored by dual channel oscilloscopes set in a X/Y configuration : Lissajous figures can show, in real time, possible deteriorations or loss in the quality of audio signals.

Phase management is also taken seriously by the Hi-Fi audio industry which, as everyone knows, emphasizes the necessity to check the phase/grounding of all loudspeakers before they are connected to a stereo system.
 
 

Lissajous figures
----------------------
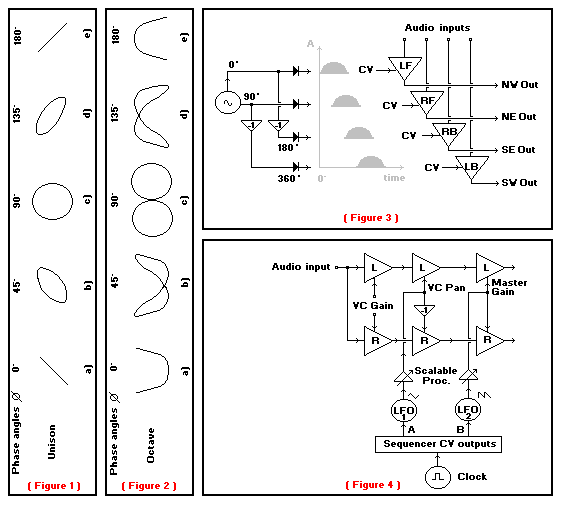
In Figure 1, a X/Y Lissajous figure, generated by a dual channel oscilloscope, shows the various angular phases of two tones in unison. Example 1a shows the configuration when both tones start at a zero degree angular moment in time.

As the phase is altered, the straight line passes through a long oblique ellipse (1b), until the difference of phase becomes a quarter of a period or 90 degrees (see 1c). Then, as the phase increases, it passes through a new oblique ellipse in another direction (1d) until it reaches the value of half-a-period or 180 degrees phase (see 1d).

In Figure 2, another Lissajous figure shows the various angular phases of two sounds, one being the upper octave of the other. Example 2a shows the configuration when both tones start at a zero angular moment in time.

Again, as the phase is altered, the cup-like form is transformed into a sort of loose rubber band configuration (Figure 2b) until the difference of phase reaches a quarter of a period or 90 degrees (notice the typical number "8" configuration in Figure 2c).
Then, as the phase increases to 135 degrees (Figure 2d), it reverses the direction of the shape in 2b,until it reaches the value of half-a-period or 180 degrees phase (Figure 2e).

Note : phase beatings and phase instability might occur when the two tones reach 45 degrees and 135 degrees phases. Phase syncing, with no beats, is achieved at zero degree and 90 degrees phase.
 

Phase Shifting

Very popular in the 60's, the Phase Shifter is a module which uses a series of 90 degrees phase shift circuits, which are set in a bucket-brigade configuration. Four circuits are needed to phase shift one stage of the original signal by a 360 degrees angle.

Typically, commercial phase shifters can deliver up to three stages of processing. In most cases, the original signal is mixed with the various processed outputs: i.e 360, 720 and 1080 degrees phase shift outputs.

Another example of dramatic Doppler and phase shifts effects, is the good old Leslie loudspeaker rotating system: complex phase shiftings and amplitude modulations(AM) are achieved in the rotating process.

In general, phases do not directly affect the overall "musical quality" of simple tones. However, during filtering, frequency-dependent phase shifts are occuring in the processed signals. For example, in an High-pass configuration, the output signal leads the input signal by 45 degrees phase, while in a Low-pass configuration the output signal lags the input signal by 45 degrees phase.
 

Spatial trajectories

Alas, a lot of e-music composition, produced nowadays, often lack a spatio-temporal quality: It is not rare to hear a CD containing a wall of sounds recorded only in Mono!. Indeed, too many e-music composers record their work with their mixing console volume pots set at maximum value and all individual panpots set at 12 o 'clock!

There is no reason to continue these bad habits : subtle sound trajectories in space add new dimensions to any e-music composition.

Thanks to the Cochlea's angular phase discrimination and the spatio-temporal qualities of interpretation of our right neo-cortex, a listener can easily determine, with precision, the spatial location of a panned sound.

Figure 3 shows the classical way to achieve a perfect rotation of a sound in a Quadraphonic field, using a sine oscillator with Quadrature outputs (the two outputs are 90 degrees out of phase).
This is easily realized with a VCF set in a ringing mode (High Q resonance, with the filter frequency set very low) and by feeding back the Band-pass output into the filter signal input. Also, two inverters are used to achieve the full 360 degrees phase shifts. Finally, the four individual outputs are half-wave rectified in a diode array and sent to the VC inputs of four VCA's..

For the lucky ones, among you, who own a Serge equal power Multi-Channel Quadraphonic mixer (QMX), patch the Low-Pass and Bandpass outputs, which are perfectly 9O° out of phase, to two scalable processors whose outputs are connected, respectively, to the horizontal and vertical VC inputs of a Quad Panner Channel (QPC). That done, set the Pan pot at 1 o'clock and the master gain pot at 12 o'clock.

As a rule, the location and trajectory speed of a sound in a stereo field or Quad space depends on the VC waveform's shape, frequency, relative amplitude and angular phase characteristics.

In order to Pan different trajectories of sounds in a stereo field one can, for example, use two different waveforms, having different frequencies and phases, to
voltage control the two VCA's. Depending on the X/Y trajectory angles and positionning in the stereo field, one can obtain good results with sine, triangular, sawtooth and, of course, with the indispensable variable slew modules.

Figure 4 shows a patch which can be used for Left/Right panning automation in a stereo field.

This is the explanation of the patch : a slow clock-driven sequencer, with at least two rows of control voltages, is used as an automated controller: Sequencer CV outputs A and B are patched to the 1 volt/oct. inputs of two LFO's having a different frequency and phase.

LFO1 triangular waveform output is sent to a scalable processor, whose output is sent to the VC pan input of a VCA (Left channel) and to a standard -1 inverter (for a 90 degrees phase shift), whose output controls the VC pan input of the second VCA (Right channel).

LFO2 sawtooth waveform output is patched to another scalable processor, whose output controls the Master gain of the two Master VCA's.

In this patch, the various potentiometers of sequencer rows A and B control the frequency of the two LFO's for each step. Also, the two scalable processors control the ratio of Left/Right angular panning (X plane) vs. the amount of master gain depth (in the Y and Z plane)

This configuration can be put to good use for smooth glides and/or dramatic trajectories of complex sounds in a stereo field.
 

André Stordeur
1.10.2003