As everyone knows, a sound is perceived when the human ear is subjected to a series of alternate compressions and rarefactions of the air,
above and below the ambient pressure, at rates of ca. 15 to 17000 times per second.

In an earlier column, called "Ear Training", we saw that it's not always easy to estimate the exact pitch of a given sound. Obviously, it is even more difficult to calculate the "virtual pitch" of a low frequency oscillator, whose frequency is less than A0= 27.5 Hz (the first key of the Grand Piano).

Hereunder, is an illustration showing virtual pitches in the lower octaves, for the values C and G, using a VCO tuned to an initial frequency
of A0 = 27.5 Hz and controlled by a standard 1 Volt/oct. keyboard. (see example 1 and 2).
 
 

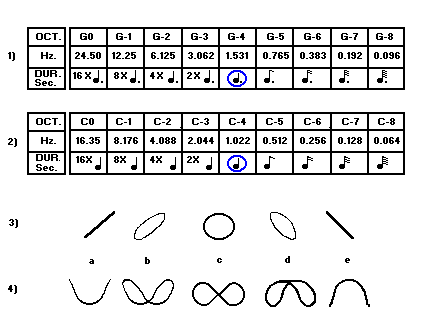
Notice, that G-4 octave has a value of 1.5 Hz. Similarly, 1 Hertz, or one beat per second, equals approximately the value of C-4 octaves. Also, notice the acceleration/decelleration factors when switching from one octave to another.

Let's take an example : What is the "virtual" pitch and harmonics distribution of a triangular LFO beating at 0.06 Hz.? Answer: the virtual pitch is C-8 octaves. Now that we know the fundamental frequency, we can easily calculate the odd harmonics of this triangular waveform (ref.chart "Composing in n Dimensions").
 

Pendular Motions
-----------------------------
In general, any waveform oscillation can be caracterized as a pendular motion: i.e the frequency of the waveform remains unchanged as
long as there is no energy loss. When the oscillation is suddenly interrupted, it becomes damped : i.e there is a gradual energy loss until oscillation stops.

For example, an LFO sine with a value of 6 Hz. (G-2 octave) can be used to control the vibrato (FM) or the tremolo (AM) of a given sound. But, other frequency ranges can be used advantageously for "growling" FM/AM effects or to instill a certain d*g*t*l flavor in an analog sound. These square waveforms, whose typical frequencies range from 12 Hz. to 24.5 Hz., are often situated at the boundaries between unpitched low frequencies and near-pitched audio
frequencies.

Evidently, knowing the virtual pitch value of a low frequency oscillator is also important for determining the right tempo for your clocking purposes. Timewise, some tempi just don't fit with the melodic aspects. Why? : Because the clock's frequency is not related to a value of C-n octaves and/or there are some minute timing deviations due to shape variations in the selected waveform used!

Depending on the caracteristics of your synthesizer, gating/triggering is achieved when using a positive -or negative- square/pulse waveform.
You can also use a triangle or sawtooth -or other variable waveforms- but, first, check if your system can be triggered by a positive or negative ramp : i.e the ascending or descending slope of the waveform determines where the trigger will occur.

Phase Relationships
----------------------
In illustration # 3, a Lissajous figure shows, in X/Y, the various angular phases of two sounds in unison. In this case, there is an oblique line if both
sounds pass through their position of rest at the same moment in time (see 3a). As the phase alters, the straight line passes through a long oblique ellipse (3b), until the difference of phase becomes a quarter of a period or 90 degrees (see 3c). Then, as the phase increases, it passes through a new
oblique ellipse in another direction (3d) until it reaches the value of half a period or 180 degrees phase (see 3d).

In illustration # 4, a Lissajous figure shows, in X/Y, The various angular phases of two sounds, one being the upper octave of the other.
For example, in illustration 4c, both sounds pass through their position of rest at he same time, while example 4b and 4d differ from that position
by 1/12 th. and example 4a and 4e by 1/4th. of the wave having the highest frequency.

In general, phase does not affect the overall quality of a sound. However, phase relationship is extremely important in mixing sounds together :
if two signals of identical frequency but unequal amplitude are out of phase, their summation will cause a partial cancellation of the mixed signals.
Also, if two signals are of identical amplitude and 180 degrees out of phase, their summation will result in complete cancellations of the two sounds.

Evidently, phase is also important in VC Panning and Cross Fading of sounds between two channels: the location and trajectory speed of a sound in a stereo field or Quad space depends on the waveform's shape, frequency, amplitude and angular phase characteristics of the controlling signals.
 
 

Andre' Stordeur
8/7/2001