 Cette partie traite de l'ALSEP, cet ensemble d'appareils de mesure que les astronautes auraient emmené avec eux, qui permettraient de faire des expériences diverses sur la lune, et d'enregistrer des données scientifiques à partir des mesures effectuées. Lien vers le document de la NASA décrivant l'ALSEP Le but de cette partie est de montrer que ces expériences n'étaient pas aussi sérieuses qu'il semble. |
 Ceci est le diagramme simplifié de l'ALSEP. Nous allons en voir plus en détail certaines parties. |
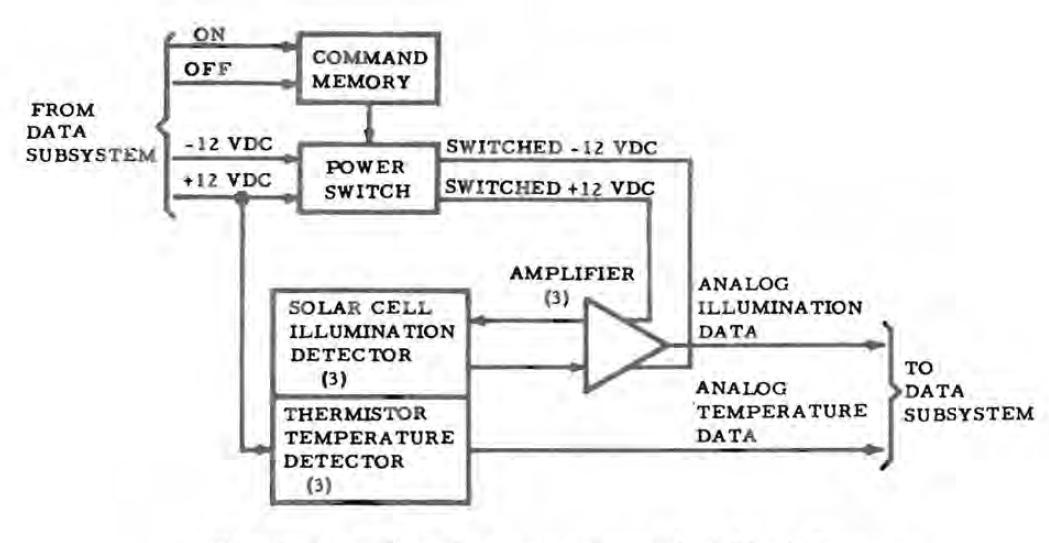 Ceci est supposé être le schéma du détecteur de poussière de l'ALSEP. |
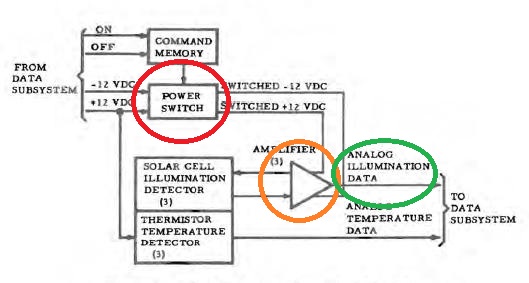 Une commande permet d'activer ou désactiver un interrupteur d'alimentation qui permet d'alimenter un amplificateur de donnée d'illumination. Mais pourquoi ne pas simplement ignorer la donnée d'illumination lorsqu'elle n'est pas désirée? |
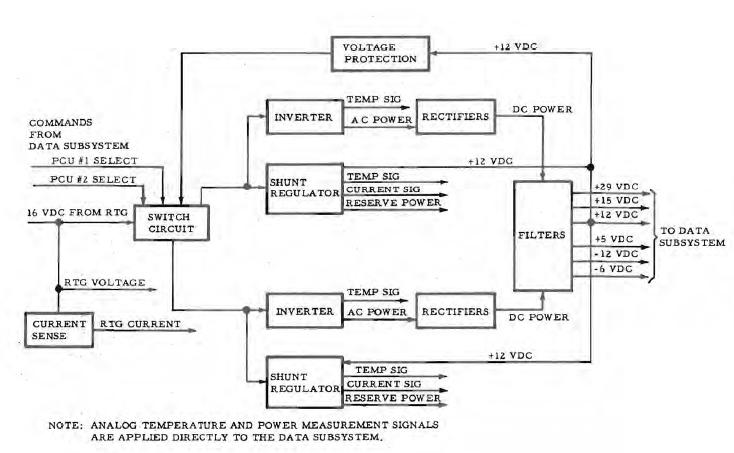 Ceci est le diagramme de fonction de génération de puissance de l'EPS. |
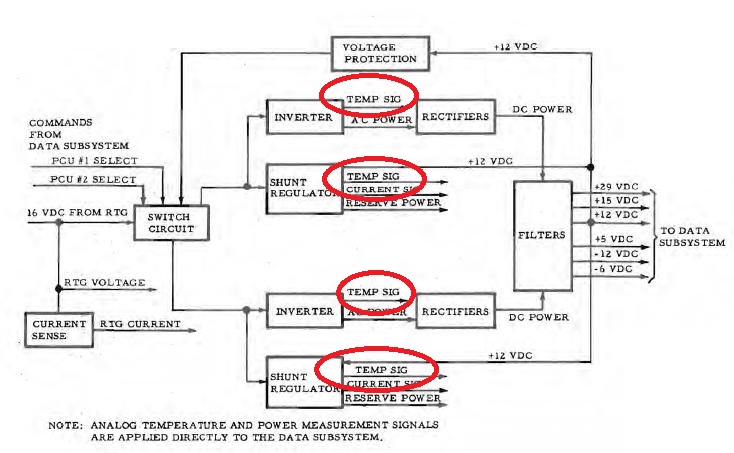 Ce que je voudrais savoir est comment un régulateur de shunt ou un inverseur peuvent générer un signal de température (cerclés de rouge). |
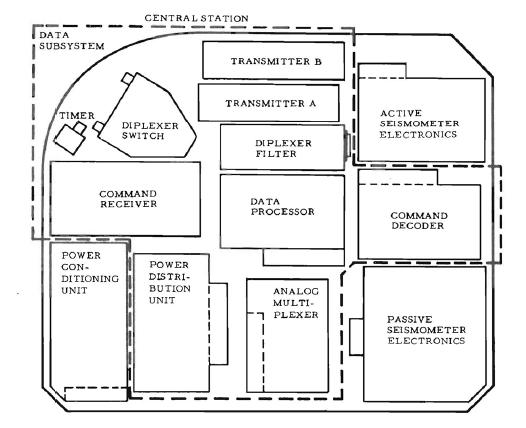 Ceci montre l'emplacement des composants du sous-système de données. |
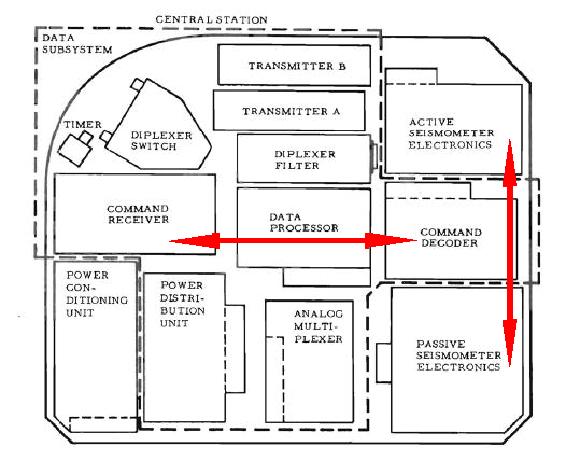 Normalement, les composants devraient être placés de manière logique, ce qui signifie que les composants qui ont un rapport entre eux devraient être proches l'un de l'autre. Pourtant, le décodeur de commande qui suit le récepteur de commande en est séparé par le processeur de données qui n'a pas de rapport direct avec le récepteur de commande. Puis les seismomètres actif et passif, qui sont tous deux des appareils de mesure, sont séparés par le décodeur de commande, ce qui place le bloc électronique du seismomètre actif plus loin du multiplexeur analogique auquel, comme le seismomètre passif, il est relié. |
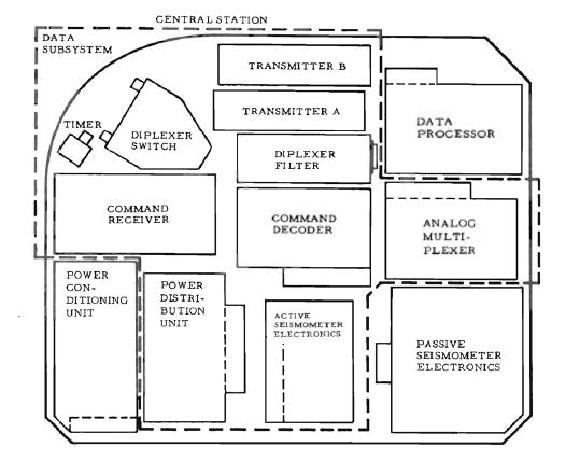 Sur ce diagramme corrigé, je montre une disposition plus logique des blocs de la station centrale. |
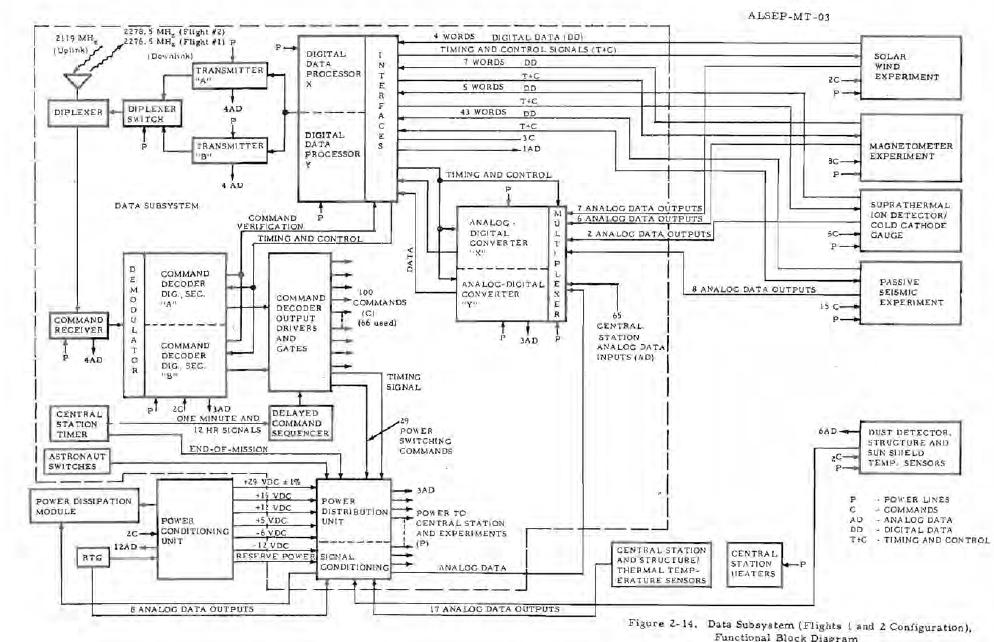 Ceci est le diagramme fonctionnel du sous-système de données. |
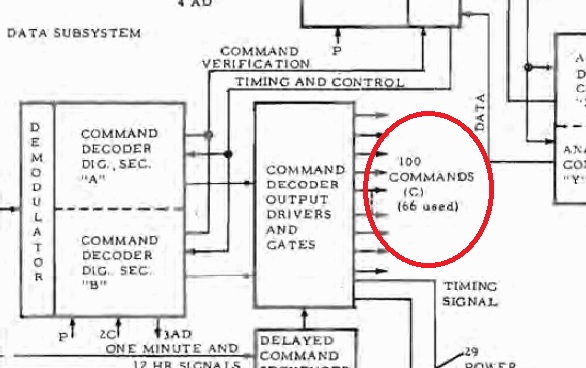 Le décodeur de commande peut fournir jusqu'à 100 commandes, dont 66 sont effectivement utilisées. Pourtant, pour encoder 66 commandes, il faut 7 bits, et, avec 7 bits, il est possible d'encoder jusqu'à 128 commandes. Alors, pourquoi restreindre à 100 le nombre de commandes possibles? Ils donnent l'explication suivante dans la documentation de l'ALSEP: "Le décodeur de commande est capable d'accepter 128 commandes différentes et est prévu pour fournir 100 commandes aux utilisateurs de l'ALSEP; Tous les codes de commande sauf les suivants sont disponibles pour les utilisateurs: 0, 1, 2, 4, 8, 14, 16. 22,24,32,29,41,49,63, 64, 78, 86, 88, 95,103,105, 111, 113,119, 123, 125. 126, 127." Mais, pourquoi est-ce que certains numéros ne peuvent être utilisés comme commande? Ces numéros interdits ne sont même pas consécutifs! S'il était vraiment nécessaire de réserver des commandes pour un usage spécial (lequel?), ces commandes devraient au moins avoir été consécutives! Ils disent aussi ceci dans la documentation: "Il a été prévu d'incorporer au décodeur de commande un maximum de 114 commandes discrètes qui ont été allouées comme suit: a. Expérimentations 62 b. Distribution de puissance 29 c. Unité de conditionnement de puissance 2 d. Processeur de données 5 e. Décodeur de commande 2 f. Disponible pour de besoins de test 14" Mais pourquoi le décodeur de commande aurait-il besoin de numéros de commande pour lui-même? La fonction du décodeur de commande est de décoder des commandes, il n'a pas l'usage de commande pour lui-même! |
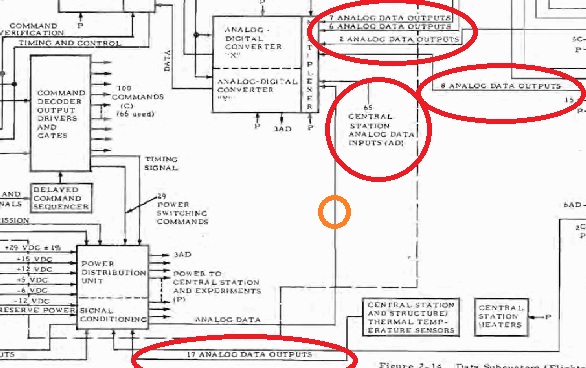 Si nous comptons les sorties analogiques de données rentrant dans le multiplexeur analogique, nous obtenons: 76+2+8+17+65=105. (Il y a 17 sorties, cerclées d'orange, venant de la station centrale, en passant par le bloc de conditionnement de signaux) |
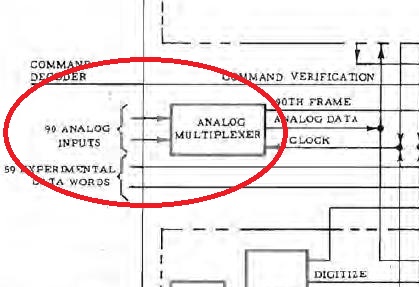 Pourtant, dans le diagramme du processeur du sous-système de données, seules 90 sorties analogiques sont indiquées rentrant dans le multiplexeur analogique. Où sont passées les 15 autres? |
 Les appareils d'acquisition reçoivent des informations numériques depuis la station centrale; ceci signifie qu'ils sont capables de décoder cette information numérique et d'exécuter l'information qu'elle contient. Mais, si ces appareils ont l'intelligence pour décoder une information numérique, ils pourraient aussi avoir l'intelligence pour encoder de l'information numérique. Ceci signifie qu'ils pourraient multiplexer leurs données analogiques, les convertir en digital, et les sérialiser dans un message numérique qu'ils pourraient envoyer à la station centrale. Quel est l'avantage d'envoyer les données sous forme numérique? D'abord cela permettrait de réduire le cablage, car le message numérique pourrait être envoyé sur un fil unique au lieu d'avoir à envoyer les données sur autant de fils qu'il y a de données à envoyer, et vu la longueur du cable de connexion, moins il y a de fils, mieux c'est; eventuellement le cable d'envoi de l'information numérique pourrait être doublé par sécurité. Puis, cela permettrait l'éviter la dégradation des données qui sont envoyées vers la station centrale; l'envoi de données analogiques à travers un si long cable a beaucoup de chance de résulter en perte de signal qui pourrait affecter les données analogiques, et les modifier; ceci pourrait être évité par l'envoi de message numérique. |
 Ceci est le diagramme fonctionnel du décodeur de commande du sous-système de données. |
 Il y a d'abord un bit de registre à décalage (cerclé de vert) qui rentre dans le comparateur de parité (cerclé de bleu), ce qui est normal, mais le train sérialisé de bits NRZ (cerclé de rouge) rentre également dans le comparateur de parité, ce qui est beaucoup moins normal. Normalement, le bit de parité du registre à décalage devrait être comparé avec un calcul de parité effectué sur les autres bits du registre à décalage. Le signal NRZ ne représente pas spécifiquement une parité, il représente une succession rapide de bits (encodés sur trois niveaux). |
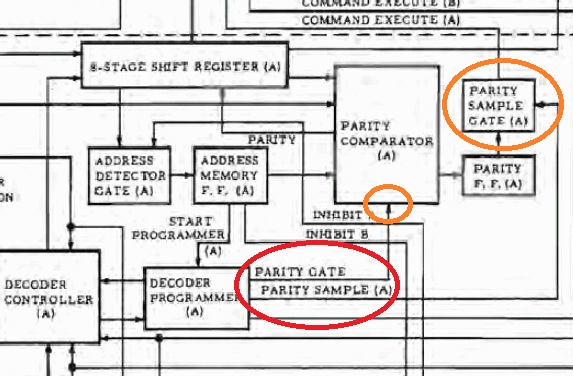 Puis le programmateur du décodeur génére deux signals, "parity gate" et "parity sample", qui permettent de valider la comparaison de parité. Mais ces deux signaux sont inutilement rendondants; l'un des deux aurait suffi à valider la comparaison. |
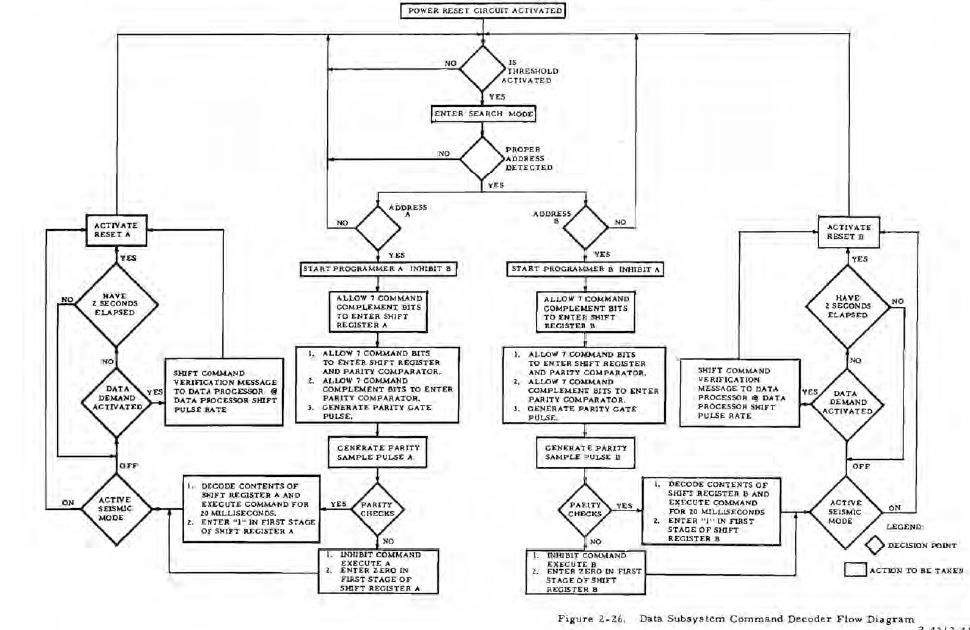 Ceci est l'organigramme du décodeur de commande du sous-système de données. |
 Cet organigramme fait d'abord une détection de l'adresse de la commande pour voir si elle est correcte, ce qui signifie que ce doit être soit une adresse A, soit une adresse B; si ce n'est aucune des deux, elle la rejette, et si c'est l'une d'elles elle l'envoie dans les deux blocs de traitement des adresses A et B; le bloc de traitement de l'adresse A la traite si c'est une adresse A et la rejette dans le cas contraire; de même le bloc de traitement de l'adresse B la traite si c'est une adresse B, et la rejette dans le cas contraire. En fait, c'est inutilement compliqué. |
 En effet, cela pourrait être simplifié en faisant cette correction: L'adresse est d'abord testée pour voir si c'est une adresse A, et traitée comme une adresse A si c'est le cas, et sinon est testée pour voir si c'est une adresse B, et traitée comme une adresse B si c'est le cas, et sinon rejetée. Mais pouquoi faire simple quand on peut faire compliqué, comme on a l'habitude de dire! |
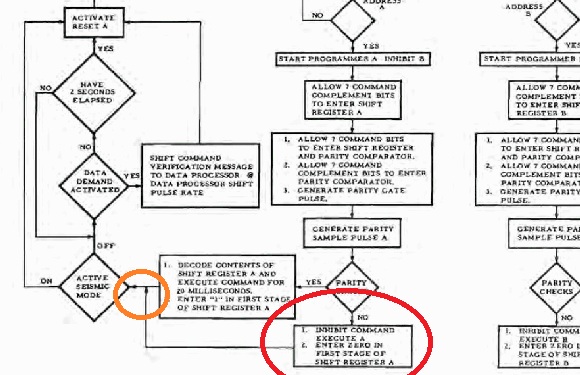 Puis, si le test de parité échoue, la commande n'est pas exécutée, et marquée comme échouée (par le bloc cerclé de rouge). Mais elle est encore soumise au message de vérification de commande par le processeur de donnée. Notez que l'éxécution de la commande n'a pas échoué, mais que tout simplement il n'y a pas eu de traitement de commande du tout, puisque le système ne savait quelle commande exécuter. |
 Normalement, si la commande n'a pas été détectée comme valide pour échec du contrôle de parité, il serait plus logique qu'elle ne soit pas soumise au message de vérification de commande par le processeur de données; seules les commandes qui ont été exécutées soit correctement, soit incorrectement, devraient être soumises à la vérification de commande par le processeur de données, pas les commandes inconnues non traitées. |
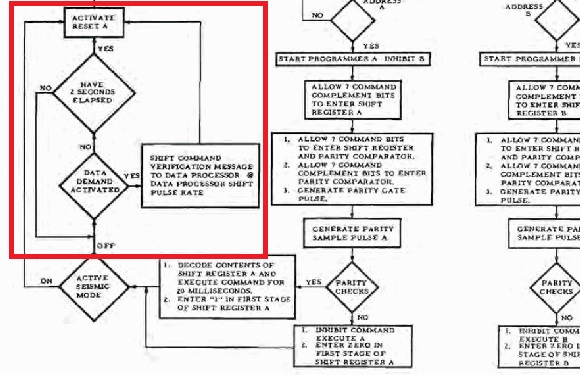 Si la demande de donnée n'a pas été detectée activée après deux secondes, la commande de vérification de message est annulée. Bien sûr, une commande ne devrait pas bloquer le traitement d'une autre commande arrivante, mais pourquoi ne pas simplement attendre jusqu'à ce qu'une autre commande arrive avant d'annuler la commande de vérification de message? Supposez que la commande suivante arrive une minute plus tard (ou une heure); la commande de vérification de message est annulée seulement après deux secondes, alors qu'il aurait été possible d'attendre une minute puisqu'aucune commande n'arrive avant une minute? C'est complétement absurde. Le time-out de deux secondes devrait seulement être appliqué si une autre commande est en attente; autrement la boucle pourrait attendre jusqu'à l'arrivée de la commande suivante. Bien sûr, si la commande suivante met trop de temps à arriver, il pourrait être désirable d'appliquer un time-out, mais alors plus élevé que deux secondes. |
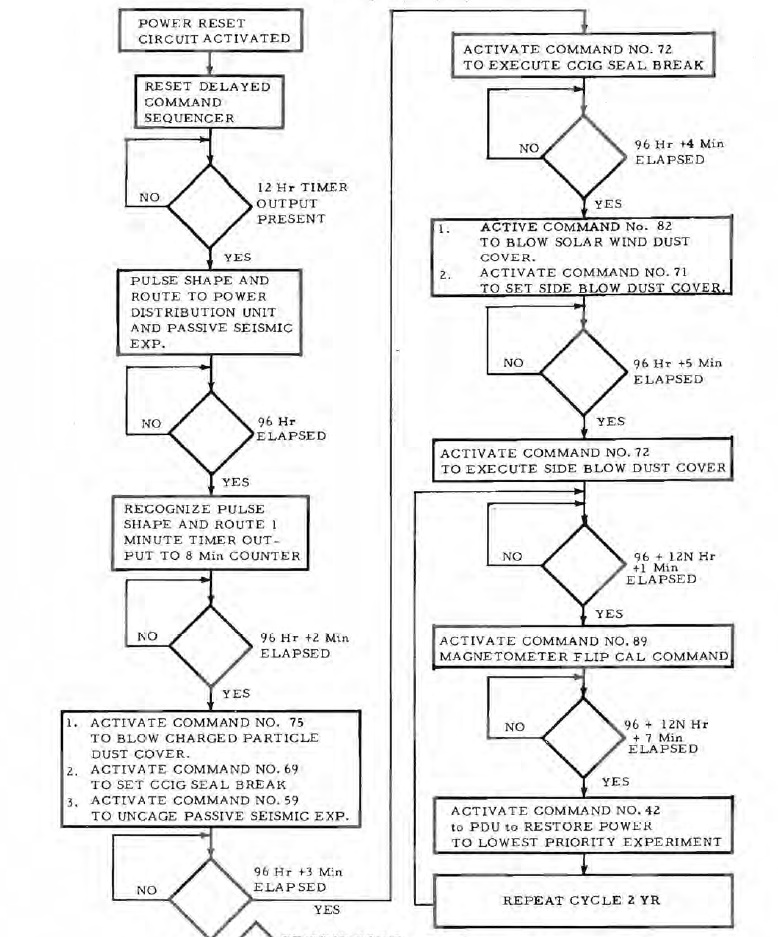 Ceci est le diagramme fonctionnel de commande retardée du sous-système de données. Cette séquence permet de faire périodiquement des commandes de maintenance (sur un cycle de deux ans). La première commande de maintenance est appliquée 96 heures après l'échéance de la période de maintenance, puis des séquences de commandes sont consécutivement exécitées, en les séparant par des pauses d'une minute. Mais c'est complétement absurde, toutes les commandes de maintenance pourraient parfaitement être exécutées sans les séparer par des pauses. Insérer toutes ces pauses entre les séquences de commandes n'a pas de sens, c'est une complication inutile. Mais, comme il a déjà été dit, pourquoi faire simple quand on peut faire compliqué! |
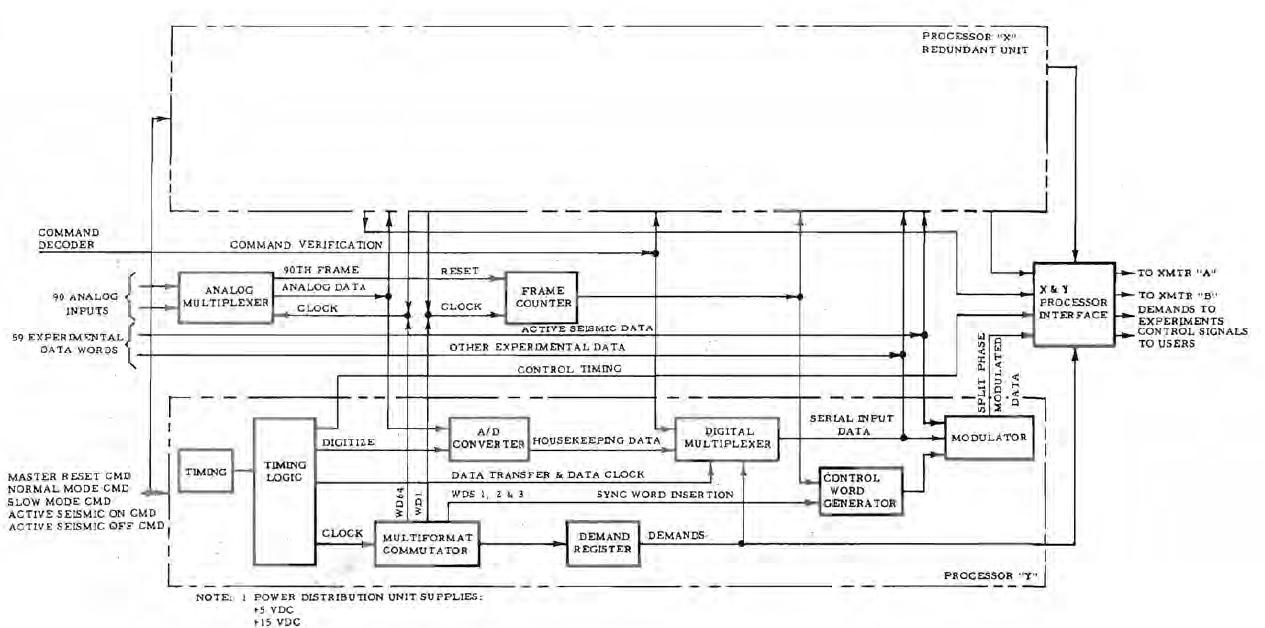 Ceci est le bloc fonctionnel du processeur de données du sous-système de données. Je dois d'abord donner quelques explications pour rendre plus clair les anomalies. |
Lorsque plusieurs informations digitales doivent être transmises dans un message numérique, cela fonctionne de la manière suivante: - Un multiplexeur digital sélectionne successivement l'information digitale à transmettre. - A chaque fois qu'une information digitale a été sélectionnée par le multiplexeur, celle-ci est sérialisée, en utilisant ce qui s'appelle un registre à décalage, de manière à créer un train de bits. - Puis le train de bits rentre dans un modulateur, dans lequel il module une porteuse de haute (et même très haute) fréquence qui permet de le transporter dans l'espace. |
Lorsque plusieurs données analogiques doivent être transmises, et que chaque donnée analogique doit être transmise sous forme numérique dans un message qui contient aussi un numéro de trame et un identificateur, chaque donnée analogique est successivement sélectionnée par un multiplexeur analogique, puis convertie en digital par un convertisseur Analogique/Digital, puis le marqueur de la donnée, le compteur de trame et la donnée convertie sont successivement transmis dans le message numérique. |
 La première anomalie est que le multiplexeur analogique génére un signal de "90ème trame" pour réinitialiser le compteur de trame à chaque fois que le compteur de trame atteint 90. Mais c'est absurde, le multiplexeur analogique ne dispose pas d'information pour réinitialiser la compteur de trame; seul le compteur de trame lui-même a cette information, et c'est à ce compteur de se réinitialiser lui-même lorsqu'il atteint un compte de 90. |
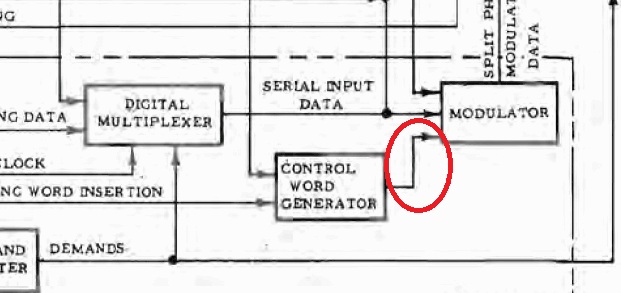 Puis, la seconde anomalie est que la sortie du générateur de mot de contrôle (control word generator), qui génére une trame à partir du mot de synchronisation (Sync Word) et du compteur de trame rentre directement dans le modulateur en même temps que les données sérialisées en provenance du multiplexeur digital. Mais cela ne peut pas fonctionner ainsi; le modulateur ne peut pas moduler deux trains séparés de bits; le modulateur devrait recevoir un train unique de bits contenant les parties successives du message à transmettre. |
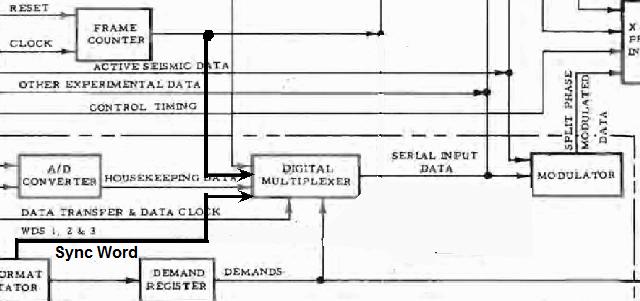 Ceci est la manière dont cela devrait fonctionner: Le mot de synchronisation et le compteur de trame rentrant dans le multiplexeur digital, de sorte que le multiplexeur puisse successivement sélectionner les parties consécutives du message et les sérialiser (le bit de parité peut être calculé au fur et à mesure de la construction du train de bits et transmis en dernier); le train de bit créé rentre ensuite dans le modulateur dans lequel il module une porteuse de haute fréquence. |
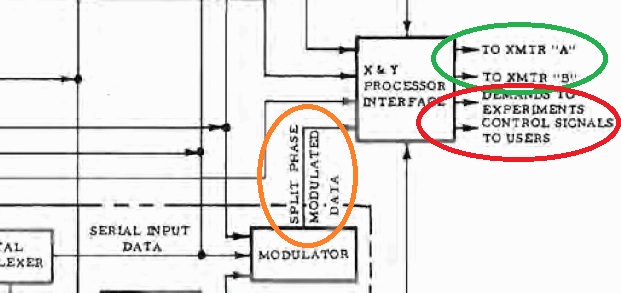 Puis le bloc "X&Y processor interface" reçoit le signal modulé et sort les signaux de transmission "XMTR A" and "XMTR B", ce qui est normal. Mais qu'ont à faire les sorties "Demandes d'expérimentation" et "signaux de contrôle" à faire avec ce bloc? |
 Dans le mot de contrôle du message, nous trouvons deux fois le marqueur du message, une fois en normal, et une fois en forme complémentée. Ils disent que le marqueur est suivi de son complément dans un but de synchronisation. Mais c'est complétement absurde de faire la synchronisation de cette manière: Supposez qu'un bit de soit le marqueur, soit son complément soit incorrectement transmis, et le début du message sera loupé. Il existe un bien meilleur moyen de faire de la synchronisation: Dans le format NRZ, un bit à 1 représente un niveau donné, et un bit à 0 un autre niveau donné; il existe un troisième niveau à zéro pour pas de bit transmis, et ce niveau zéro, qui n'est ni un bit à 1, ni un bit à 0, peut être utilisé pour séparer les trames, et les synchroniser; il peut être répété pour assurer une sécurité totale du message; c'est un moyen bien plus sûr de synchronisation que de complémenter le marqueur qui rend seulement le message plus long sans vraiment le sécuriser. |
 Ceci est l'antenne de l'ALSEP qui transmet à la terre les informations que la station centrale reçoit des appareils qui lui sont reliés, et aussi reçoit des commandes depuis la terre. De manière à fonctionner de manière correcte, l'antenne doit être orientée de manière aussi précise que possible vers la terre.  Nous voyons un gros-plan de cette antenne sur la photo AS17-134-20491.  Ceci est la description du mécanisme de visée dans la documentation de l'ALSEP. 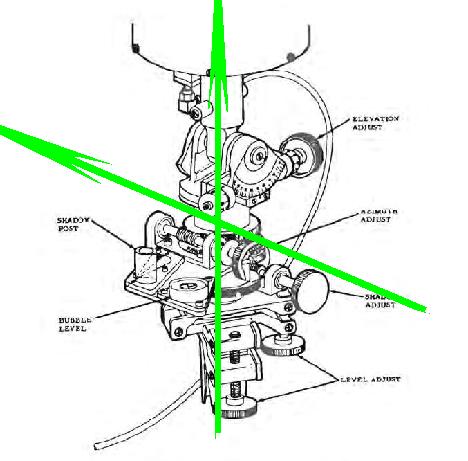 De manière à être orientée vers la terre, l'antenne devait être orientée autour de deux axes, un horizontal (pour régler un angle appelé "Elevation"), et un axe vertical (pour régler un angle appelé "Azimut"). Pour ce faire, les astronautes devaient suivre les instructions suivantes. 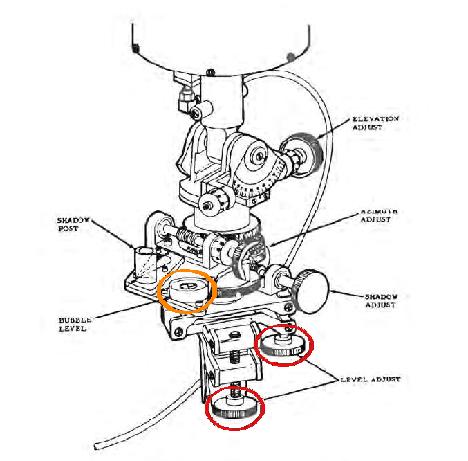 Ils devaient faire d'abord un réglage pour régler horizontalement le niveau de l'antenne par niveau à bulle avec les deux molettes que j'ai cerclées; l'horizontalité était obtenue lorsque la bulle d'air était centrée dans son cercle.  Et un réglage pour orienter l'antenne relativement au soleil en faisant un réglage d'ombre. Le but était de mettre l'antenne dans un système de référence lune/soleil. Mais pourquoi faire ce réglage, pourquoi ne pas simplement viser la terre avec l'antenne? L'explication qui est donnée par la NASA est que la terre n'a pas une position parfaitement fixe dans le ciel lunaire, mais sa position varie un peu dans une zone de libration. Donc, si l'antenne est orientée pour pointer vers la position courante de la terre, lorsque la terre est sur le point opposé de la zone de libration, la réception serait moins bonne; de manière à avoir toujours une réception satisfaisante, le mieux est d'orienter l'antenne, non vers la courante position de la terre, mais vers le centre de la zone de libration. 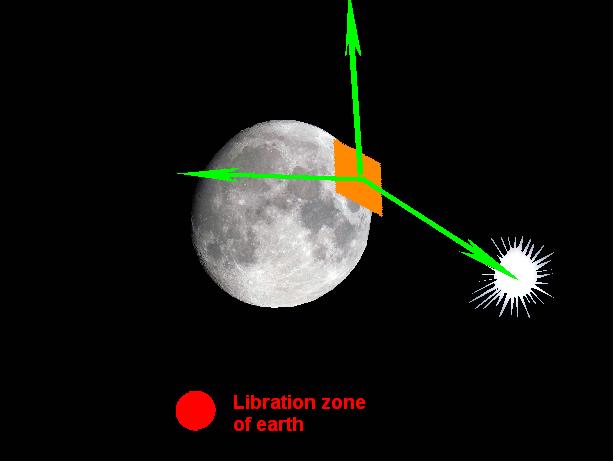 Les réglages de l'horizontalité lunaire et l'ombre solaire permettraient de placer l'antenne dans un système référentiel qui serail dans un plan localement tangentiel à la lune, et suivant la longitude locale. La NASA calculerait alors les angles du centre de la zone de libration relativement à ce système de référence et les indiquerait sur la checklist de l'astronaute; une fois que l'astronaute a fait les réglages pour placer l'antenne dans le système de référence lune/soleil, l'astronaute a juste à régler les deux molettes supérieures sur les angles prédéterminés de sa checklist, sans avoir à viser la terre. Fantastique!  Résumons donc: L'astronaute régle d'abord l'horizontalité relativement à la lune avec les molettes 1 et 2; puis il fait un alignement d'ombre avec la molette 3; et alors il n'a plus qu'à mettre les molettes 4 et 5 sur les valeurs prédéterminées indiquées sur sa checklist: pas besoin d'orienter l'antenne vers la terre. Et c'est supposé être un réglage précis? Le réglage d'horizontalité avec le niveau à bulle est loin d'être précis. Donc, même si les angles sont spécifiés avec beaucoup de précision (deux décimales), un réglage fait à partir d'une référence imprécise reste imprécis. 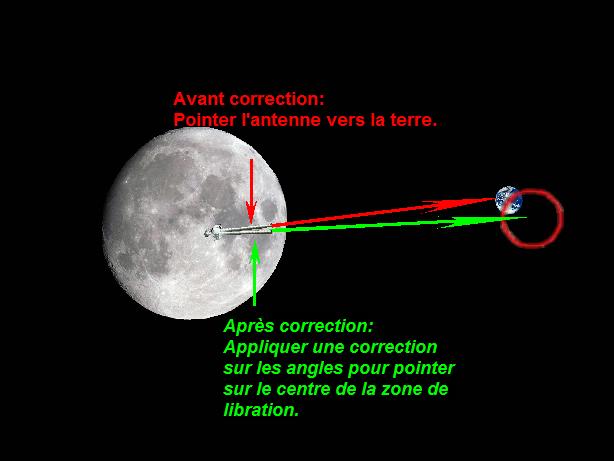 Pourquoi n'ont-ils pas simplement pointé l'antenne vers la terre, et puis fait une correction sur l'azimut et l'élévation (avec des valeurs fournies sur la checklist) pour que l'antenne soit orientée vers le centre de la zone de libration à la place; seul un réglage de l'horizontalité aurait été nécessaire, celui du soleil aurait été ignoré. 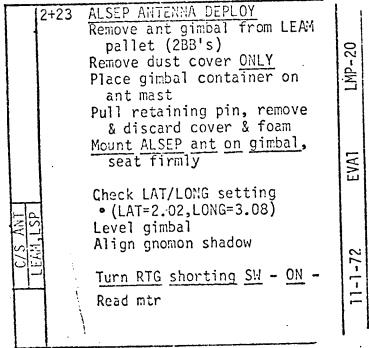 Les angles de réglage de l'antenne indiqués sur la checklist d'Apollo 17 semblent plutôt bas. 2,02° de latitude est vraiment un angle faible pour une latitude.  Cela placerait la terre juste au-dessus de l'horizon, bien plus bas ce que nous voyons sur les photos de la mission.  Vous remarquerez que les angles indiqués sur la checklist sont les valeurs de la latitude et la longitude du site d'alunisage d'Apollo 17 divisées par 10. Quelqu'un a suggéré que celui qui a préparé la checklist voulait en fait dire la latitude et longitude du site d'alunissage au lieu de leur dixième, mais cela ne pouvait de toute façon pas être la latitude et longitude du site, et je vais expliquer pourquoi. 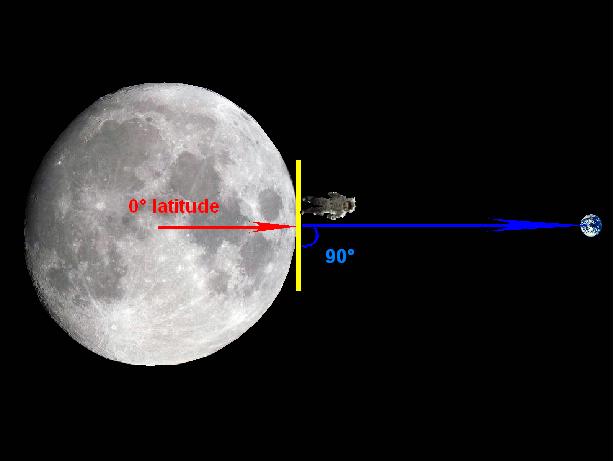 Si le site d'alunissage était à l'équateur de la lune, sa latitude serait de 0°, et la terre serait à la verticale du site d'alunissage (ou plus exactement le centre de sa zone de libration); les astronautes verraient la terre juste au dessus de leurs têtes, et la latitude de la terre relativement au site d'alunissage serait de 90°. La barre jaune sur mon schéma représente l'orientation du plan horizontal local. Et ne ne vous étonnez pas que j'aie fait la terre bien plus petite que la lune alors qu'elle est en réalité plus grosse, car je ne la représente pas avec sa vraie taille relativement à la lune, mais à la manière dont elle est vue depuis la lune.  A la longitude 0, une fois obtenue l'horizontalité de la base de l'antenne, l'antenne devrait être tournée d'un angle égal à la latitude relativement à la verticale locale pour pointer vers la terre.  Mais le réglage de l'élévation ne se fait pas à partir de la verticale, mais de l'horizontale.  Mais l'angle de la direction de la terre relativement à la verticale locale n'est égal à la latitude que lorsque la longitude est nulle; la longitude contribue également à accroître cet angle, et donc à diminuer l'élévation de la terre relativement au site. Si la latitude est nulle et la longitude égale à 20°, la terre sera vue avec la même élévation que lorsque la latitude vaut 20° et la longitude est nulle. Alors, que se passe t-il avec l'élévation lorsque la latitude et longitude sont toutes deux non nulles, ce qui est le cas pour le site d'alunissage d'Apollo 17? Et bien, c'est un peu plus compliqué. 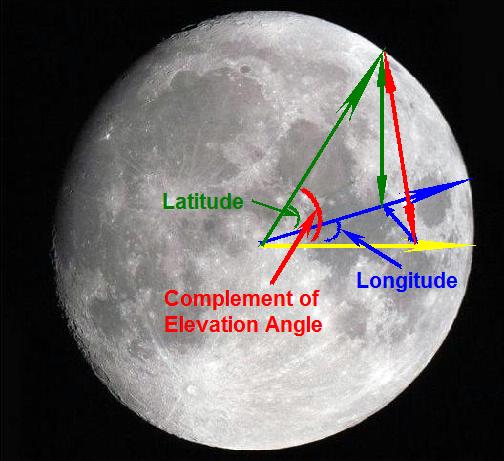 J'utiliserai les notations suivantes pour mes explications: - J'appelle R le rayon de la lune. - J'appelle L la longitude. - Jappelle l la latitude. - Et j'appelle e l'angle que le rayon local fait avec l'axe de référence du système sélénographique (le rayon de latitude et longitude nulles), qui est également l'angle que la direction de la terre fait avec la verticale locale. La perspective que j'ai choisie pour mon schéma peut faire apparaître les angles différents de ce qu'ils sont (par exemple, la double flèche bleue est perpendiculaire au rayon jaune, même si elle n'apparaît pas ainsi); mais c'était nécessaire pour représenter toutes les composantes sans qu'elles se cachent l'une l'autrre. Dans le système de coordonnées sélénographique, le site d'alunissage a deux coordonnées: - Une coordonnée horizontale qui peut être calculée à partir de la longitude et est représentée par la double flèche bleue sur mon schéma, et qui est égale à R*sin(L). - Une coodonnée verticale qui peut être calculée à partir de la latitude, et est représentée par la double flèche verte sur mon schéma, et qui est égale à R*sin(l). - La distance du site d'alunissage (représentée par la double flèche rouge sur mon schéma) à l'axe de référence peut être calculée à partir des coordonnées du site en utilisant le théorème bien connu de Pythagore; elle est égale à: Racine carrée((R*sin(L))²+(R*sin(l))²)=R* Racine carrée(sin(L)²+sin(l)²). Mais cette distance peut aussi être calculée à partir de l'angle que le rayon local fait avec l'axe de référence, celui qui nous intéresse; cette distance est aussi égale à R*sin(e). Nous obtenons finalement la formule qui nous donne l'angle e à partir de la latitude et la longitude: e=asin(Racine carrée(sin(L)²+sin(l)²)); ceci représente l'angle que la direction de la terre fait avec la verticale locale, et l'angle d'élévation est donc le complément à 90° de cet angle. Finalement la formule pour calculer l'angle d'élévation à partir de la latitude et longitude s'établit comme: Angle d'élévation angle=90°-asin(Racine carrée(sin(Longitude)²+sin(Latitude)²)) Avec les latitude et longitude du site d'alunissage d'Apollo 17 (respectivement 20.2° et 30.8°) cette formule donne un résultat égal à 52° pour l'angle d'élévation. Vous voyez donc que l'angle d'élévation n'a pas de relation directe avec la latitude, et que la longitude contribue à le modifier.  L'angle d'azimut est l'angle entre la direction horizontale de la terre telle que vue depuis le centre de la lune que nous voyons, et la direction horizontale telle que vue depuis le site d'alunissage. Il augmente avec la longitude et diminue inversement avec la latitude. L'angle d'azimut est positif lorsque compté dans le sens des aiguilles d'une montre et négatif lorsque compté trigonométriquement quand la longitude est Est, et c'est l'inverse quand elle est Ouest. La formule pour calculer l'angle d'azimut est: Angle d'azimut=asin(R*cos(Latitude)*sin(Longitude)/R)=asin(cos(Latitude)*sin(Longitude)) Avec les latitude et longitude du site d'Apollo 17, cela donne: Angle d'azimut=asin(cos(20.2)*sin(30.8))=29°. Vous voyez donc que les angles d'élévation d'azimut pour régler l'antenne après l'avoir placée dans le système de référence lune/soleil sont loin d'être directement la latitude et la longitude comme un fan d'Apollo le pensait.  Donc, même si celui qui a préparé la checklist à déplacé le point décimal parce qu'il voulait en fait indiquer les latitude et longitude du site d'alunissage, comme suggéré par un fan d'Apollo, cela reste faux, car les angles d'élévation et d'azimut de l'antenne sont différents de la latitude et longitude du site d'alunissage, et sont des fonctions plutôt compliquées d'à la fois la latitude et la longitude.  Selon Clavius lui-même, l'angle de vue vertical des photos d'Apollo serait de 53.5°; c''est assez proche de l'angle d'élévation de la terre au site d'alunissage d'Apollo 17 (52°); cela signifie que la distance entre l'horizon et le centre de la terre est assez proche de la hauteur de la photo, à peine moins. Lorsque l'horizon appraraît au bas de la photo, le terre apparaît tout près du haut de la photo. Sur cette photo, AS17-134-20387, si je prolonge la ligne d'horizon, et que je trace une line perpendiculaire à cette ligne qui croise la terre, et que je compare la distance de la terre à la ligne d'horizon avec la hauteur de la photo, ces deux distances sont assez proches; la distance de la terre à la ligne d'horiuzon est à peine plus petite que la hauteur de la photo, comme cela doit être le cas, dont la position de la terre semble cohérente sur cette photo. Cela confirme l'angle d'élévation que j'ai calculé.  Maintenant, sur cette photo, AS17-137-20957, cela sonne très différemment. La terre semble vraiment très basse relativement à l'horizon. Si nous comparons la distance de la terre relativement à l'horizon et la comparons avec la hauteur de la photo, nous en déduisons que la terre serait seulement à un angle de 20° relativement à l'horizon: 20° au lieu de 52°! Alors qu'est ce qui est arrivé à la terre sur cette photo? Maintenant, des fans d'Apollo m'ont fait remarquer que cette photo est prise au massif du sud, et que ce nous voyons serait la ligne de crête du massif, qui est nettement plus haute que la ligne d'horizon, et non la ligne d'horizon elle-même; cela expliquerait la proximité de la terre relativement à cette ligne.  Mais il y a deux autres photos sur lesquelles nous voyons aussi la terre basse relativement à la ligne de fond, avec le même rocher, très reconnaissable, qui apparaît dessus; celle de gauche de la vue stéréoscopique est référencée AS17-137-20960, et celle de droite est référencée AS17-137-20961. Si nous comparons les deux rochers, celui de la second photo est un peu plus petit, car j'ai mesuré la distance entre deux mêmes points du rocher sur les deux photos, et trouvé quelle était un peu plus petite sur la seconde photo (plus petite de 5 millimètres sur mon affichage). Cela signifie que le photographe a reculé entre les deux photos; mais, s'il recule, et est orienté en direction de la pente montante, cela signifie qu'il descend la pente et donc s'abaisse relativement à la ligne de crête; cela signifie aussi que la ligne de crête devrait se rapprocher de la terre sur la deuxième photo. Mais, lorsque je mesure la distance de la terre à la ligne de crête sur les deux photos (sur la deuxième photo, j'ai du prolonger la partie de la ligne qui est cachée par le rocher), au lieu de trouver une distance plus courte sur la deuxième photo, je trouve une distance plus longue à la place; plus longue seulement de 2 ou 3 millimètres, mais c'est assez pour dire qu'elle est plus longue. Nous avons une claire contradiction ici. La libration de la terre ne pourrait agir si rapidement. Si la NASA avait vraiment voulu faire les choses sérieusement, elle aurait fait l'antenne de l'ALSEP suivre automatiquement la terre (par test de réception optimale); si la NASA était capable de contrôler à distance l'orientation de la caméra TV de la rover, pourquoi ne pourrait-elle pas en faire autant pour l'antenne de l'ALSEP? |
 Et, franchement, lorsque nous voyons l'ALSEP sur la photo AS15-86-11592, il ressemble vraiment à une pièce de quincaillerie qui est totalement incapable de faire la moindre mesure et de transmettre la moindre information. |
 Les appareils connectés à l'ALSEP mesuraient des données et les transmettaient à la station centrale qui les transmettait vers la terre où elles étaient enregistrées et tracées. Je vais montrer des singularités sur ces tracés. |
 Ce tracé rassemble les mesures faites par plusieurs appareils de l'ALSEP d'Apollo 12 pendant le lever de soleil de la mission. |
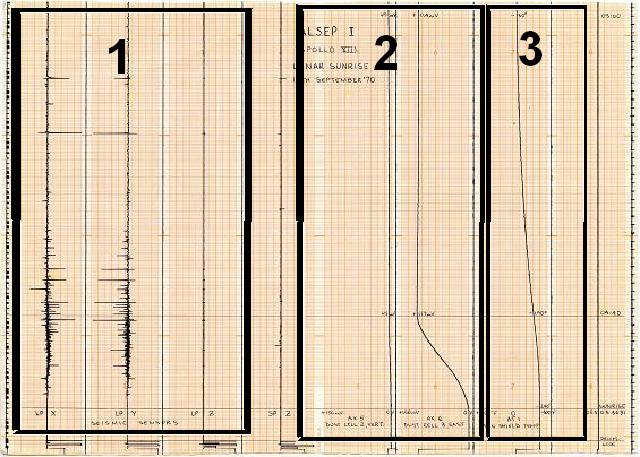 Je montrerai successivement les différentes parties de ce tracé. |
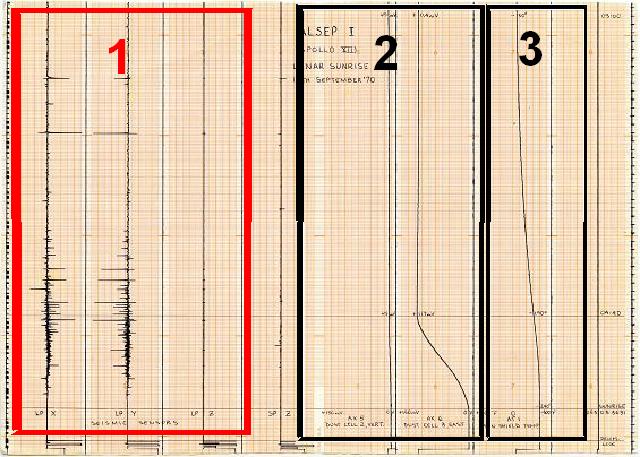 Pour commencer la section 1 rassemble les données d'un séisme lunaire le long des trois composantes spatiales X, Y, et Z (X et Y en horizontal, et Z en vertical). |
 Nous voyons les tracés du séisme pour chacune des trois composantes spatiales. |
 Ce qui est surprenant est que la mesure le long de la composante Z est complètement plate (ou pratiquement), ce qui signifie que le séisme s'est exclusivement produit dans un plan horizontal. |
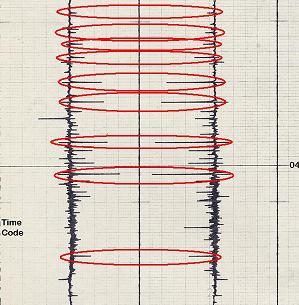 De plus nous voyons presque une symétrie entres les tracés X et Y; les pics de X et Y sont le plus souvent synchronisés et restent dans la même direction. Cela signifie que le séisme lunaire ne se serait pas seulement exclusivement produit dans un plan horizontal, mais aussi principalement le long d'une direction donnée. |
 Nous allons maintenant nous intéresser aux mesures des cellules de poussière lunaire. |
 Les données mesurées par la première cellule de poussière montrent une lente progression de la poussière, mais la mesure reste plutôt faible. |
 Inversement, les données mesurées par la seconde cellule de poussière progressent très rapidement en comparaison, ce qui signifie que cette cellule détecterait beaucoup plus de poussière lunaire que l'autre. Peut-être était-elle plus exposée au vent lunaire! |
 Il y a un autre fait étonnant à propos de cette seconde cellule de poussière. Alors que sa mesure progresse d'abord très rapidement, non seulement elle se stabilise, mais elle commence même à décroître un peu. Donc, après avoir rapidement accumulé de la poussière lunaire, elle commencerait à en perdre? Qu'est-ce qui s'est passé? Le vent lunaire a commencé de balayer sa poussière? |
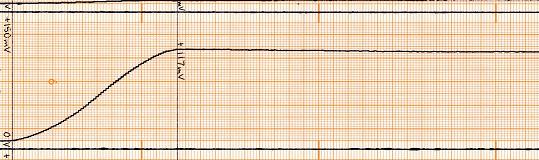
 Nous allons d'abord nous intéresser à la partie concernant la température de l'écran solaire. |
 La température de l'écran solaire paraîtrait presque normale... |
 ...si elle ne commençait pas à changer seulement après une période d'inertie. Pourquoi n'a t'elle pas commencé de changer immédiatement après le début de la mesure? Est-ce qu'elle dormait pendant ce temps? |
 Et la dernière mesure reste constamment plate. On peut de demander s'il était vraiment nécessaire de l'enregistrer. |
 Ceci est le tracé du second séisme qui s'est produit durant la mission d'Apollo 12. Cette fois, les tracées en X et Y sont plats, et le séisme se produit exclusivement verticalement. Les séismes sont très étranges sur la lune, ils sont très directionnels! |
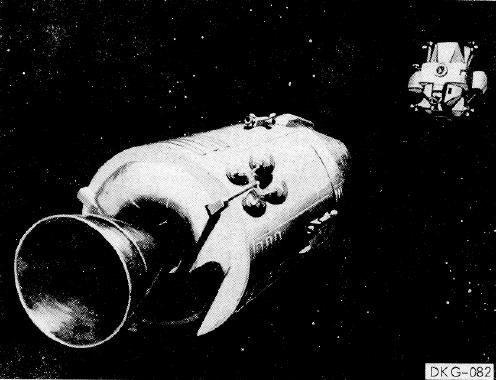 e eAprès le retour du module lunaire au module de commande, et que le LEM se soit arrimé au module de commande, le LEM fut largué. Dans Apollo 11 et Apollo 16, il fut laissé en orbite autour de la lune, mais, dans les autres missions, Apollo 12 inclus, une maneuvre de sortie d'orbite fut faite sur le module lunaire pour le faire s'écraser sur la lune, afin de faire enregistrer son crash par les séismomètres de l'ALSEP. Pendant la descente vers la lune, de manière à gagner une orbite inférieure, le module lunaire décroît sa vitesse; ceci est supposé lui faire prendre une orbite elliptique qui le fait se rapprocher de la lune à l'autre bout de l'orbite elliptique; ils disent que le module lunaire perd environ 75 pieds/s pour attraper l'orbite qui l'amène à l'orbite inférieure, à une altitude de 50000 pieds (15 km), à l'autre bout de l'orbite elliptique. Cela signifie que la vitesse orbitale du module de remontée du module lunaire devrait être suffisamment réduite, de sorte que l'orbite elliptique, que cette réduction lui fait prendre, devienne trop courte et coupe la lune. J'ai calculé qu'une réduction de 85 pieds/s (~100km/h) place le module lunaire sur une orbite qui touche la lune à l'autre bout de l'orbite (i.e. altitude 0). Cela signifie que la réduction nécessaire de vitesse pour faire le module lunaire s'écraser sur la lune devrait être supérieure à 85 pieds/s. Si le module lunaire ne fait rien, il ne s'écrasera pas sur la lune.  Le rapport de mission d'Apollo 12 dit que la maneuvre de sortie d'orbite fut contrôlée à distance, elle n'était pas pré-programmée après la séparation.  Le problème est que la commande de sortie d'orbite devait être envoyée pratiquement une demie orbite avant le site d'alunissage pour que le module lunaire s'écrase près de celui-ci, Et, comme le site d'alunissage est sur la face visible de la lune, cela signifie que le module lunaire était sur la face cachée de la lune lorsque la commande sortie d'orbite devait être envoyée; cela signifie que la lune était entre l'émetteur et le module lunaire lors de l'envoi de la commande de sortie d'orbite; pas une situation idéale pour que le module lunaire puisse recevoir l'ordre de sortie d'orbite. OK, supposons que le module lunaire puisse recevoir la commande de sortie d'orbite en dépit des mauvaises conditions de réception, et que le module lunaire puisse l'exécuter.  Hamish Lindsay dit à propos de l'impact du module lunaire d'Apollo 12 sur la lune: "Lorsque le module lunaire d'Apollo 12 frappa la surface lunaire à 6048 km/h, à 72 kilomètres du site d'alunissage, creusant un cratére estimé à 9 mètres de large, les résultats furent étonnants. Les 3 séismomètres de l'équipement enregistrérent l'impact, ce qui généra une séquence de réverbérations durant presque une heure." Et il montre le graphe enregistré de l'événement. Mais, en fait, lorsque le module lunaire s'écrase sur la lune, il a une vitesse horizontale très importante, mais une vitesse verticale relativement modérée, l'importante vitesse horizontale crée en effet une vitesse centrifuge qui contre la plus grande partie de l'attraction lunaire, et permet à la vitesse verticale d'augmenter seulement modérément. Cela signifie que le module lunaire s'écrase sur la lune presque horizontalement; il égratigne la surface lunaire plutôt que de creuser un cratére local profond. Dans l'atmosphère terrestre, cela aurait été bien différent, parce que l'atmosphère ralentit l'importante vitesse horizontale qui se convertit en vitesse verticale à la place. Si la lune avait eu une atmosphère comme la terre, le module lunaire aurait frappé la surface lunaire verticalement avec une vitesse élevée. Mais la lune n'a pas d'atmosphère pour ralentir l'importante vitesse horizontale du module lunaire, et c'est donc surtout horizontalement que le module lunaire heurte la surface lunaire. D'ailleurs, le fait que le module lunaire frappe la surface lunaire presque horizontalement est confirmé par cette phrase dans le rapport de mission d'Apollo 12: "L'angle entre la trajectoire d'impact et la surface lunaire moyenne était de 3,7 degrés au point d'impact." 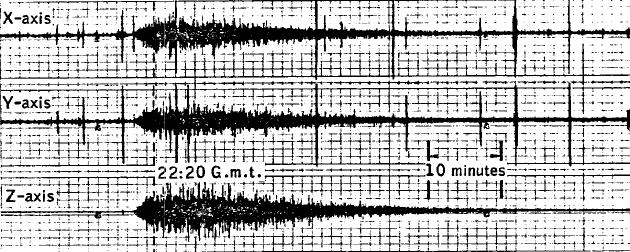 Pourtant, si nous examinons les tracés des trois séismomètres sur les trois axes (que j'ai trouvés dans le rapport de mission d'Apollo 12 - Lindsay ne nous montre que celui suivant l'axe vertical), nous voyons que le tracé suivant l'axe vertical a plus d'amplitude que ceux suivant les axes horizontaux, Alors que cela devrait être l'inverse puisque, comme je l'ai mentionné, l'impact du module lunaire sur la surface lunaire était principalement horizontal. Conséquemment, ce sont les tracés suivant les axes X et Y qui devraient montrer la plus grande amplitude, et le tracé suivant l'axe Z nettement moins (son amplitude devrait avoir environ le dixième de l'amplitude des tracés horizontaux). |
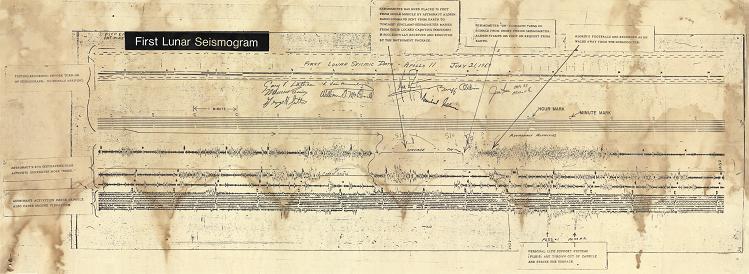 Ceci est le premier séismogramme d'Apollo 11. On dirait un vieux parchemin du moyen-âge! |
 Ces gens semblent dire: "Mais qu'est ce que c'est que ce merdier!" |
Je doute que cette station de comédie ait pu jamais enregistrer quoique ce soit! |