L'improbable voyage vers la lune

Le principal obstacle pour envoyer des hommes sur la lune est la barrière des ceintures de Van Allen
Les hommes ne pourraient survivre aux radiations dans ces ceintures sans être efficacement protégés, et il est évident que le module de commande n'offrait pas cette protection.
Les fans d'Apollo essaient de minimiser l'effet de ces radiations, et disent que les astronautes auraient du faire un long séjour dans ces ceintures pour vraiment en souffrir.

Le 28 juin 1969, deux mois avant le lancement d'Apollo 11, un vaisseau spatial a été lancé dans l'espace, lequel contenant un singe appelé Bonnie, pour une mission planifiée sur un mois. L'objectif de la mission était d'étudier l'effet de l'espace sur un être vivant. Cependant, après seulement neuf jours en orbite, la mission fut stoppée à cause de la santé défaillante du sujet. Bonnie mourut huit heures après avoir été récupéré en raison d'une attaque cardiaque due à la déshydratation.
En dépit de cet échec prouvant le danger de l'espace sur les humains, Apollo 11 fut lancé à peine deux mois plus tard, avec prétendument des humains à l'intérieur, sans avoir fait de tests supplémentaires!

Ce n'est pas la seule occasion dans laquelle la NASA a montré un singulier manque de test avant de risquer des vies humaines.
la NASA rapporte que, pendant Apollo 10, il y a eu d'importantes oscillations observées sur une pile à combustible; ces oscillations auraient pu provoquer la panne de la pile à combustible, et la NASA dit que c'est une chance que cela ne se soit pas produit dans Apollo 10.

La descente vers la lune est la partie la plus périlleuse de la mission lunaire; si une pile à combustible faisait défaut dans la descente, ce serait plus critique que si cela arrivait au module de commande orbitant la lune; cela pourrait avoir des conséquences dramatiques pour les astronautes.

Sur terre, ils ne furent pas capables de reproduire le problème, mais ils observèrent de petites perturbations isolées sur la pile à combustible dont ils supposérent qu'elles étaient en rapport avec ce problème; ils imaginérent une solution pour ce problème, mais, comme le problème ne se produisait que dans l'environnement lunaire, la seule manière sûre de savoir si le problème avait vraiment été résolu aurait été de faire le test dans l'environnement lunaire, ce qui aurait signifié envoyer une autre mission pour tester le comportement de la pile à combustible.

Au lieu de cela, la NASA a directement envoyé la mission suivante, Apollo 11, se poser sur la lune, sans être totalement sûre que le problème avait été résolu pour la pile à combustible, et qu'elle était à l'abri d'une panne.
Elle s'est reposée sur la "chance".

Des astronautes s'approchant des ceintures de Van Alen, sans les pénétrer, ont rapporté avoir éprouvé des phénomènes visuels dus aux radiations, apparaissant comme des étoiles filantes.
Mais les astronautes d'Apollo, ainsi que l'a rapporté Alan Bean, n'ont pas rapporté un tel phénomène, quoiqu'ils aient supposément traversé complètement ces ceintures.

Robert Braeunig a montré une trajectoire que le module de commande aurait prise, et qui lui aurait permis d'éviter la partie dangereuse des ceintures de Van Allen, et aurait épargné ses radiations aux astronautes.
Cette trajectoire a été montrée par de nombreux adeptes d'Apollo, comme si c'était parole d'évangile, et nul ne doute que le module de commande ait réellement pris cette trajectoire...Le problème est qu'il n'y a pas le moindre document du temps d'Apollo qui confirme cette trajectoire...et, encore pire, je vais montrer qu'il y a un document qui la contredit.

Le document que je prends comme référence pour contredire la trajectoire préconisée par Braeunig est un document titré "Apollo Launch Windows".

Ce document montre les trajectoires qui auraient été prises par les fusées Saturn.

Mais ce qui nous intéresse ici est la trajectoire sur laquelle aurait été placé le module de commande.
Le document établit clairement que cette trajectoire dépend de la position de la lune sur son orbite.
Cette position n'est pas constante, et, alors que le module de commande voyage, la lune se déplace sur son orbite.
Donc, de manière à optimiser la trajectoire, et faire le minimum de maneuvres, le but est de diriger le module de commande non vers la position courante de la lune, mais vers celle qu'elle aura au moment où le module de commande l'atteindra.

Donc, le S-IVB, alors qu'il orbite la terre, fait un changement de direction pour diriger le module de commande vers sa destination finale, la position qu'il aura quand il atteindra la lune.

Ceci est illustré par ce commentaire dans le document:
"Transfer energy considerations. In order to arrive in the vicinity of the moon the spacecraft was 'aimed' (targeted) at a position where the moon would be at the time of its arrival as illustrated in figure 5."
soit:
"Considérations de transfert d'énergie: De manière à arriver dans le voisinage de la lune, le vaisseau spatial a été dirigé vers une position à laquelle la lune serait au temps de son arrivée, comme illustré sur la figure 5".

Le plan orbital de la lune fait avec le plan ecliptique (le plan de l'orbite de la terre autour du soleil) un angle de 5° qui est à ajouter à l'angle que le plan écliptique fait avec le plan équatorial de la terre aui est 23°, soit au total 23+5=28°.

Et, si nous traçons une direction correspondant à ce nouvel angle, nous trouvons que, à part la déviation initiale qui n'est pas mentionnée dans le document que j'ai pris comme référence, la trajectoire de Braeunig est presque parallèle à cette direction.

En fait la direction de la lune (depuis la terre) fait avec le plan équatorial un angle qui n'a absolument rien à voir avec l'angle entre le plan orbital de la lune et le plan équatorial de la terre.
L'angle de direction de la lune avec le plan équatorial est seulement égal à l'angle entre le plan orbital de la lune et le plan équatorial de la terre sur les extrêmités de l'orbite lunaire; partout ailleurs il est plus petit; après avoir atteint son sommet, il décroît, jusqu'à ce que la lune croise le plan équatorial de la terre, à quel moment il est même nul; puis il augmente de nouveau, négativement cette fois, jusqu'à ce que la lune atteigne l'autre extrêmité de son orbite, sur laquelle cet angle est à nouveau égal à l'angle entre le plan orbital de la lune et le plan équatorial de la terre, et puis il décroît de nouveau, jusqu'à ce que la lune croise à nouveau le plan équatorial de la terre, et ainsi de suite...

Le document montre un graphe représentant la direction de la lune relativement au plan équatorial comme une sinusoïde d'amplitude 28° (l'angle antre le plan orbital de la lune et le plan équatorial de la terre).

C'est pourquoi il est important d'étudier l'évolution de la lune sur son orbite de manière à déterminer la trajectoire optimisée, celle qui dirigera le module de commande directement vers la position qu'aura la lune au moment où le module de commande arrive près d'elle.

Le module de commande devrait seulement être dirigé sur une direction faisant un angle de 28° relativement au plan équatorial de la terre si le module de commande arrivait près de la lune alors qu'elle se trouve au sommet de son orbite...Mais c'est très loin d'être le cas comme nous allons le voir.
D'un autre côté, si le module de commande arrivait près de la lune au moment où elle croise le plan équatorial, il pourrait parfaitement faire le voyage dans ce plan équatorial.

Donc, tout le problème est de savoir où se trouvera la lune sur son orbire au moment où le module de commande l'atteint, de manière à déterminer la direction qu'il doit prendre au début de son voyage.
Nous savons que le module de commande d'Apollo 11 a atteint la lune le 19 juillet.
Donc, bien entendu, j'ai cherché la nouvelle lune précédente, et également l'apogée précédente, de manière à être en mesure de déterminer où elle était sur son orbite à ce moment.

Lorsque j'ai regardé les phases de la lune en 1969...

...J'ai trouvé que la nouvelle lune précédant Apollo 11 s'est produite au 14 juillet, soit 5 jours avant que le module de commande n'atteigne la lune.

Encore plus intéressant, lorsque j'ai regardé l'apogée précédant Apollo 11, j'ai trouvé qu'elle s'est produite le 13 juillet, soit 6 jours avant que le module de commande n'atteigne la lune.

Nous savons que la lune prend 7 jours pour parcourir un quart de son orbite.
De ce qui précède, il en ressort que la lune était à ce moment bien plus proche du plan équatorial de la terre que du sommet de son orbite.
Cela signifie que l'angle que sa direction faisait avec le plan équatorial était nettement moins que l'angle entre le plan orbital de la lune et le plan équatorial de la terre, même pas sa moitié (je l'estime aux environs de 8°).

Ceci est d'ailleurs confirmé dans le document que j'ai pris comme référence, lequel montre que l'angle courant de la direction de la lune au moment du rendez-vous du module de commande avec elle était manifestement bien inférieur à l'angle du plan orbital de la lune.

Donc, finalement, si je représente à présent la direction réelle prise par le module de commande telle que déterminée par sa destination finale, nous pouvons constater que le module de commande pénétrait encore davantage dans le coeur des ceintures de Van Allen que dans ma démonstration erronée précédente, et elle discrédite encore davantage la trajectoire préconisée par Robert Braeunig.

Et cela ne concerne pas qu'Apollo 11, car, dans toutes les missions, le module de commande est arrivé près de la lune alors que la lune était proche de son premier quartier.

En fait les choses se déroulaient de cette manière: Le S-IVB (le dernier étage de la fusée Saturn, contenant le module de commande et le module lunaire) utilisait son moteur puissant pour faire prendre une vitesse conséquente au vaisseau spatial permettant de sortir du champ gravitationnel de la terre, et le plaçait aussi sur la trajectoire le menant vers sa position finale, la position où se trouverait la lune lorsque le module de commande l'atteindrait.
Le vaisseau spatial suivait ensuite cette direction jusqu'à la moitié du voyage vers la lune, et alors il faisait une légère correction, appelée "midcourse correction", pour ajuster la trajectoire du vaisseau spatial vers la position de la lune au moment du rendez-vous.
Le but est de faire aussi peu de changements de direction que possible, car tout changement de direction nécessite de brûler du propergol, et l'économiser est essentiel.

Donc, de manière à connaître la trajectoire suivie par le module de commande, tout ce que nous avons besoin de savoir est les coordonnées de l'injection translunaire (faite par le S-IVB), et celles de la première correction de mi-trajet, sachant qu'entre ces deux points, le module de commande se déplace en ligne droite (ou presque).
Je montre ici les paramètres indiqués dans le rapport de mission d'Apollo 11 (montrés sur la page 7-9).
L'injection translunaire est faite à la latitude 9,98° nord, et une altitude de 180,6 milles (335 kilomètres), et la première correction de mi-course est faite à une latitude de 5,99° nord, et une distance de 109575 milles (202933 kilomètres).
Je n'ai pas mentionné la longitude, car les ceintures tournent tout autour de la terre, et donc cette indication n'est pas intéressante.
En fait, altitude signifie distance à la surface terrestre.

Sur ce schéma, seulement un quart de la distance à la moitié de la distance à la lune peut être représenté, et donc, sur son extrémité, la latitude tombe du quart de la différence de latitude entre l'injection translunaire et la première correction de mi-course.
J'ai représenté en jaune la trajectoire correspondante du module de commande, et vous pouvez constater que, contrairement à la trajectoire préconisée par les propagandistes d'Apollo, le module de commande n'évite pas du tout la partie dangereuse des ceintures de radiations.

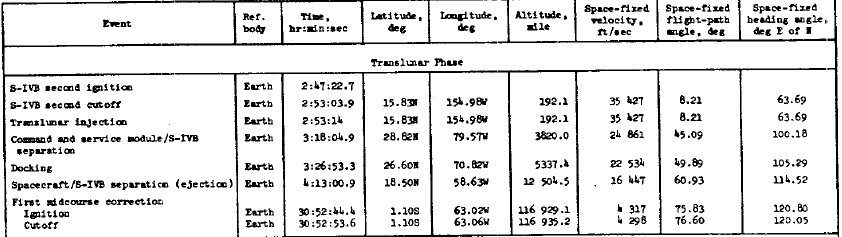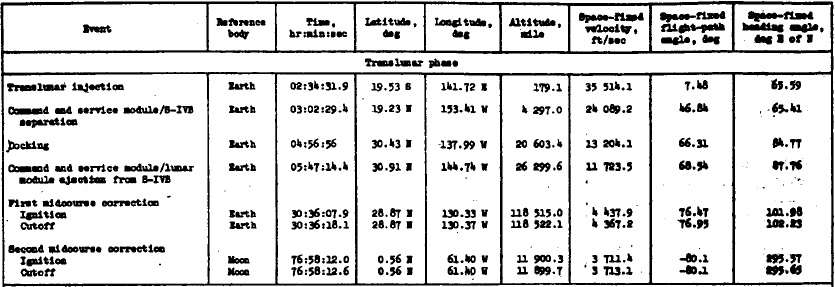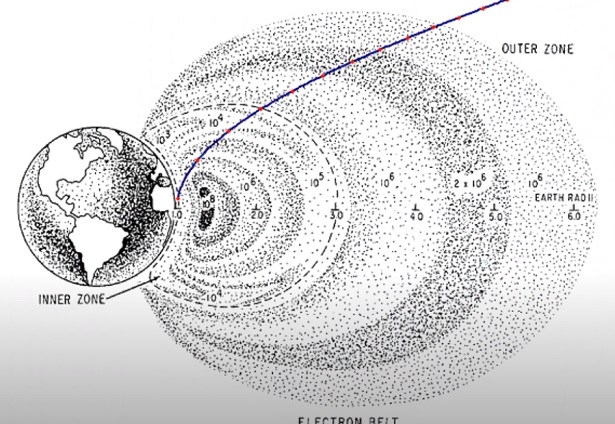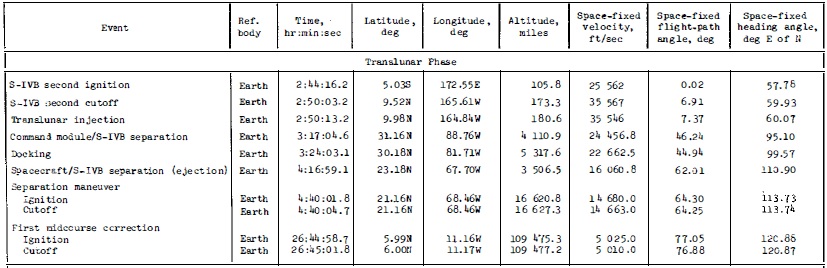
La table affiche aussi des données sur le point de séparation du module de commande du S-IVB, et aussi le point où le module de commande s'arrime au module lunaire.
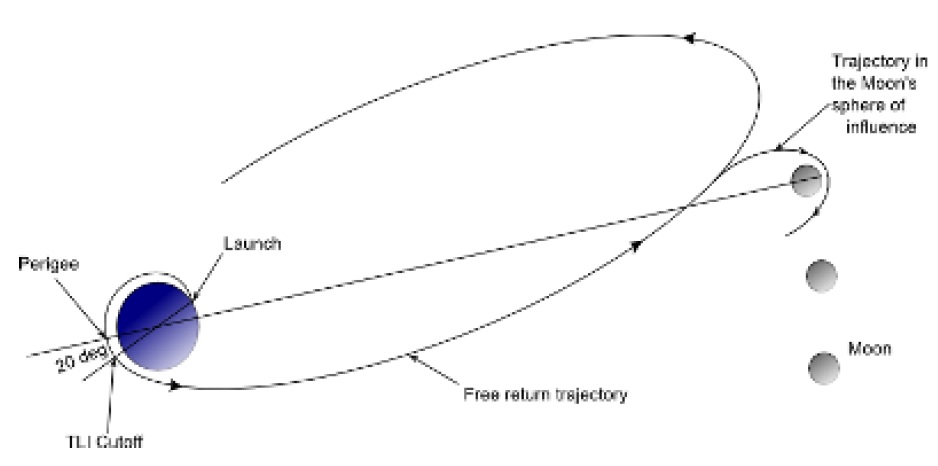
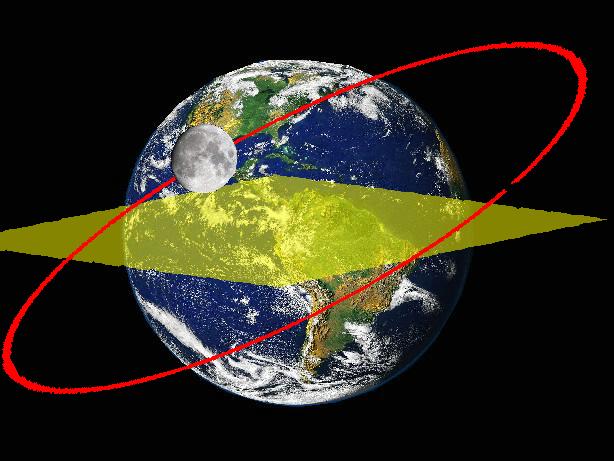
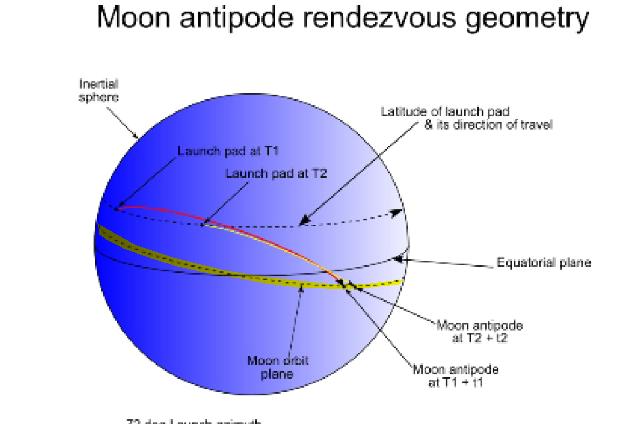
Ce que nous remarquons d'abord est que la séparation du module de commande du S-IVB se produit à une latitude de 31,16° nord, ce qui est nettement au-dessus de la latitude de l'injection translunaire, et ce qui est complètement anormal, car cette latitude devrait être proche de celle de l'injection translunaire, et même légèrement en-dessous, comme le vaisseau spatial descend à partir de l'injection translunaire, et que le le point de la première correction de mi-course est plus proche du plan équatorial; ceci est impossible, comme il n'y a pas de correction faite par le module de commande avant qu'il n'atteigne la première correction de mi-course.
Cela n'aurait aucun sens que le S-IVB envoie le module de commande dans une direction complètement fausse, qui l'aurait fait passer très loin de l'orbite lunaire, alors que le S-IVB pouvait l'envoyer directement dans la bonne direction.
A cette vitesse, un changement de direction nécessite beaucoup d'energie, et donc une consommation importante de propergol, essayez de prendre un virage serré lentement, puis rapidement, et vous verrez la différence!
Mais ce n'est pas la seule incohérence dans cette table, il y en a une autre, mais elle est plus subtile.
Selon cette table, la séparation du module de commande du S-IVB est faite à une altitude de 41110,9 milles, alors que l'arrimage du module de commande au module lunaire est fait à une altitude de 51317,6 milles; cela fait une différence d'altitude de 1206,7 milles, soit 2234,81 kilomètres.
La séparation du module de commande du S-IVB est faite au temps 3 heures, 17 minutes et 4 secondes, et l'arrimage du module de commande au module lunaire est fait au temps 3 heures, 24 minutes, et 3 secondes; cela fait 419 secondes de différence.
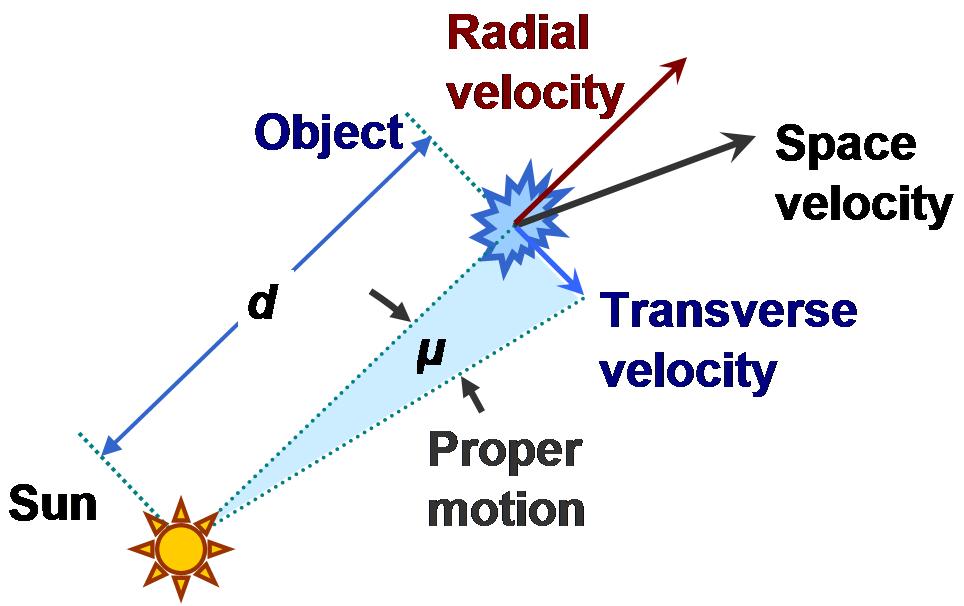
Si nous rapportons cette différence d'altitude à une heure (3600 secondes), cela ferait une vitesse radiale moyenne (i.e. vitesse dans la direction du centre de la terre) égale à 2234,81*3600/419=19201 km/h (en ignorant la partie décimale).
Mais la table donne une autre indication de vitesse dans la colonne "space-fixed velocity"; pour la séparation du module de commande du S-IVB, nous lisons 24456,8 pieds/s; en multipliant par 0,3048, nous la convertissons en m/s, et, en multipliant par 3,6, nous la convertissons en kilomètres par heure, ce qui donne 26836 km/h, mais cette vitesse est une vitesse suivant la direction courante du vaisseau spatial, et non une vitesse radiale (i.e. en direction du centre de la terre).

En fait, de manière à convertir cette vitesse en vitesse radiale, nous devons la projeter sur la direction radiale (la direction vers le centre de la terre), en multipliant cette vitesse par le cosinus de l'angle que fait la direction du vaisseau spatial avec la direction de la terre.

Dans la table, cet angle est mentionné comme "space-fixed angle", et il est indiqué comme 46,24° pour la séparation du module de commande du S-IVB.
Après avoir multiplié la vitesse trouvée par le cosinus de cet angle, nous trouvons finalement une vitesse radiale de 26836*cos(46,24°)=18867 km/h, une vitesse qui, comme vous le voyez, est très différente de la vitesse radiale précédemment trouvée.
De même, la vitesse indiquée pour l'arrimage du module de commande au module lunaire est indiquée comme 22662,5 pieds/s, ce qui donne 24867 km/h; et, en multipliant par le cosinus de l'angle avec la direction radiale, qui est égal à 44,95°, nous trouvons finalement une vitesse radiale pour l'arrimage égale à 24867*cos(44,95°)=17599 km/h.
Donc, entre la séparation du module de commande et l'arrimage du module de commande au module lunaire, nous aurions une vitesse radiale moyenne de (18867+17599)/2=18233 km/h.
Pour conclure, nous avons obtenu la vitesse radiale moyenne entre la séparation du module de commande du S-IVB et l'arrimage du module de commande au module lunaire de deux manières différentes, et, au lieu de trouver deux valeurs proches, nous avons trouvé deux valeurs très différentes, comme nous avons trouvé 19201 km/h et 18233 km/h, donc une différence de presque 1000 km/h.

C'est un indice manifeste donné par les ingénieurs.
Lorsque j'examine leurs tables, je trouve plein d'incohérences intentionnelles.
J'en ai trouvé beaucoup dans la table de la descente motorisée montrée dans un document.

Ceci est la table de paramètres pour Apollo 12 (montrée à la page 5-5 du rapport de mission).
L'injection translunaire est faite à une latitude de 15,83° nord, et une altitude de 192.1 milles (356 kilomètres), et la première correction de mi-course est faite à une latitude de 1,108° Nord, et une distance de 116929 milles (216552 kilomètres).

J'ai représenté en jaune la trajectoire correspondante du module de commande, et vous pouvez constater que, une fois de plus, contrairement à la trajectoire préconisée par les propagandistes d'Apollo, le module de commande n'évite pas du tout la partie dangereuse des ceintures de radiations.

Et, une fois de plus, la latitude du point de séparation du module de commande du S-IVB est anormalement trop haute, comme précédemment expliqué.
Il y a aussi un autre indice dans cette table de paramètres.
Au point de séparation du module de commande du S-IVB, le vaisseau spatial a une vitesse de 24861 pieds/s, ce qui donne 27279 km/h.
Au point de l'arrimage du module de commande au module lunaire, le vaisseau spatial a une vitesse de 22534 pieds/s, ce qui donne 24726,11 km/h.
Au point de l'extraction du module lunaire du S-IVB, le vaisseau spatial a une vitesse de 16447 pieds/s, ce qui fait 18046,96 km/h.
Il y a 528 secondes entre la séparation du module de commande et l'arrimage du module de commande au module lunaire, et 3018 secondes entre l'arrimage du module de commande et l'extraction du module lunaire.
Cela signifie que, entre la séparation du module de commande et l'arrimage du module de commande au module lunaire, il y aurait une perte moyenne de vitesse correspondant à 2553*3600/528=17406 km/h par heure.
Et, entre l'arrimage du module de commande au module lunaire et l'extraction du module lunaire, il y aurait une perte moyenne de vitesse correspondant à 6679,15*3600/3018=7967km/h par heure.
Cela signifie que, entre les deux premiers événements, le vaisseau spatial aurait décéléré plus de deux fois plus qu'entre les deux derniers événements.
Une absurdité qui est un indice évident donné par les ingénieurs.

Finalement, ceci est la table de paramètres pour Apollo 14 (montrée à la page 6-4 du rapport de mission).
L'injection translunaire est faite à une latitude de 15,83° Sud, et une altitude de 189,1 milles (332 kilomètres), et la première correction de mi-course est faite à une latitude de 28,87° Nord, et une distance de 118515 milles (218490 kilomètres), ce qui signifie que le module de commande croiserait le plan équatorial pendant son voyage.

Maintenant, nous trouvons encore plus d'incohérences dans cette table que dans les tables précédentes.
La latitude du point de séparation du module de commande du S-IVB est de 19,23 Nord, ce qui signifie que le S-IVB l'aurait envoyé dans une direction qui est encore plus fausse que dans les missions précédentes.
Et, après, le module de commande aurait été envoyé nettement au-dessus du plan équatorial, alors qu'il était parti en-dessous (à l'injection translunaire), il aurait été envoyé plus près du plan équatorial, car la latitude a deuxième correction de mi-course est 0,56° nord; ce n'est certainement pas une trajectoire optimisée!
Entre la séparation du module de commande du S-IVB et l'arrimage du module de commande au module lunaire, il y a presque deux heures (une heure et 54 minutes).
Pourquoi autant de temps alors que les missions précédentes n'ont eu besoin que de quelques minutes?

Mais qu'ont bien pu faire les astronautes pendant tout ce temps? Ont-ils fait une pause café et joué aux cartes?

Et, entre l'arrimage du module de commande au module lunaire et l'extraction du module lunaire du S-IVB, il y a un écart de temps de 51 minutes, à nouveau un temps important qui est difficile à expliquer.
Mais ce qui est le plus intéressant est de voir la vitesse du vaisseau spatial à chacun de ces points.
Au point de la séparation du module de commande du S-IVB, la vitesse indiquée est de 24089 pieds/s, soit 26432 km/h.
Au point de l'arrimage du module de commande au module lunaire, la vitesse indiquée était de 13204 pieds/s, soit 14488 km/h.
Et, finalement, au point de l'extraction du module lunaire du S-IVB, la vitesse indiquée est de 11723 pieds/s, soit 12863 km/h.
Cela signifie que, entre la séparation du module de commande et l'arrimage du module de commande au module lunaire, le vaisseau spatial a perdu 11944 km/h en 114 minutes, ce qui fait une perte moyenne de vitesse de 6286 km/h par heure.
Et, entre l'arrimage du module de commande au module lunaire et l'extraction du module lunaire, le vaisseau spatial a perdu 1625 km/h en 51 minutes, ce qui fait une perte moyenne de vitesse de 1912 km/h par heure.
Cela signifie que le vaisseau spatial aurait décéléré plus de 3 fois plus entre les deux premiers événements qu'entre les deux derniers, mieux que dans Apollo 12!
Ceci est bien sûr totalement absurde, et un indice évident donné par les ingénieurs.

Je ne suis pas allé plus loin qu'Apollo 14, parce que ce que j'ai lu dans les tables suivantes devenait si délirant que j'ai trouvé inutile de les exploiter.
La table de paramètres d'Apollo 15 que nous trouvons dans le rapport de mission d'Apollo 15 a été très mal scannée, et ses indications sont difficilement lisibles.
Mais, ce qui m'a frappé est que l'altitude de la première correction de mi-course, au lieu de représenter une distance proche de la moitié de la distance à la lune, représentait une distance dans l'orbite proche de la terre, et ce qui est ironique est qu'elle était encore plus proche de la surface terrestre que le point de l'injection translunaire, comme si le module de commande avait reculé à partir de l'injection translunaire!

La conclusion est que les données que nous trouvons dans les tables des missions confirment que le module de commande n'a pas pu prendre la trajectoire magique préconisée par les propagandistes d'Apollo.
Toutes les trajectoires rentrent dans le coeur des ceintures de radiations.

Le module de commande n'aurait pas pu prendre la trajectoire préconisée par les propagandistes d'Apollo, qui permet de tourner autour des ceintures de radiations, car c'est complètement contraire à un transfert minimum d'energie tel que décrit dans la documentation de la NASA.
Cette trajectoire aurait forcé le module de commande à faire de constants changements de direction, ce qui aurait impliqué de brûler du propergol.
Et cela va même au delà de ce qu'ils montrent, car après le module de commande doit redescendre vers le plan équatorial de la terre, car le point final de rendez-vous est plus proche du plan équatorial.

Et, oui, le module de commande tourne aussi autour de la lune, mais c'est complètement différent, car il suit alors une orbite naturelle, il n'a pas à fournir d'effort avec son moteur, car c'est la gravité lunaire qui fait tout le boulot de faire tourner le module de commande.

Le module de commande aurait brûlé tellement de propergol pour faire tous ces changements de direction dans la trajectoire préconisée par les propagandistes d'Apollo que le module de service aurait été à court de propergol avant même d'atteindre la lune.

Les propagandistes d'Apollo s'imaginent probablement qu'il y a plein de stations de propergol au long du voyage du module de commande où les astronautes peuvent refaire le plein de propergol!

Quoique cette trajectoire soit prouvée fausse, qu'elle est complètement contredite par la procédure suivie par le vaisseau spatial, les propagandistes d'Apollo la montrent comme la trajectoire qui aurait été suivie par le module de commande pour éviter la partie embarrassante des ceintures de Van Allen.

Par exemple Curious Droid la montre dans une vidéo où il parle du problème des radiations, comme s'il ne faisait pas de doute que le module de commande a vraiment suivi cette trajectoire.
Il fait confiance à celui qui a imaginé cette trajectoire, et pense qu'il a vérifié que le module de commande avait vraiment suivi cette trajectoire, ce qui n'est absolument pas le cas.

Et Amy Shira Teitel, la fausse spécialiste de Vintage Space, qui n'a qu'une connaissance très superficielle du projet Apollo, la montre aussi comme s'il ne faisait pas de doute que le module de commande a suivi cette trajectoire.

Et bien sûr, le fameux AstronoGeek, bien connu des français, ne fait pas exception, et lui aussi, en bon suiveur, montre cette trajectoire comme ne faisant pas de doute qu'elle ait été suivie par le module de commande pour magiquement éviter la partie dangereuse des ceintures de radiation.

Donc, toutes les démonstrations des propagandistes d'Apollo sont basées sur de la pure désinformation, car elles sont basées sur un modèle qui peut être prouvé faux et impossible; je ne dirais pas que cette désinformation est intentionnelle, car je suis sûr qu'ils croient sincérement à celle-ci, et c'est plutôt du à leur ignorance du projet, et comment il fonctionne, mais elle est factuelle.

Il n'y a pas que le voyage vers la lune qui est problématique; le retour vers la terre l'est également.

Le problème de faire une rentrée directe vers la terre est que le module de commande avait une vélocité très élevée à l'approche de la terre.
S'il ne diminue pas cette vélocité avant de pénétrer dans l'atmosphère, il a une bonne chance de surchauffer.
Ce seraient les cendres des astronautes qui seriaent récupérées, et non les astronautes vivants eux-mêmes, lorsque le module de command plongerait dans l'océan.
C'est pourquoi il était préférable de faire une rentrée rebondissante au lieu d'une rentrée directe, de manière à diminuer suffisamment la vélocité du module de commande avant de pénétrer dans l'atmosphère, de sorte que l'échauffement du module de commande reste dans des limites acceptables.
C'est ce que Chris Kraft, directeur de vol d'Apollo, a préconisé.

La rentrée rebondissante consiste à faire rebondir le vaisseau spatial sur l'atmosphère au lieu de pénétrer directement dedans, et de faire diminuer suffisamment la vélocité avant de pénétrer effectivement dedans pour la descente finale, de sorte que la vélocité restante conserve l'échauffement due à la friction atmosphérique dans des limites raisonnables.
C'est ce que les fusées russes ont fait avec succès.

Donc, alors que la NASA a montré les rentrées du module de commande comme des rentrées directes, cette rentrée aurait plutôt du être une rentrée rebondissante à la place, dit Chris Kraft.

Mais les astronautes Stafford et Al Worden ne sont pas d'accord avec ce point de vue, et insistent qu'il s'agissait d'une rentrée directe.
Al Worden est même tellement furieux contre Chris Kraft qu'il a même dit: "Chris Kraft est un salaud. Si nous pouvions l'attacher à une bombe, nous le ferions".
C'est vraiment excessif, car ce que disait Chris Kraft était complétement raisonnable.
Ceci montre que la foi des astronautes d'Apollo confine à une foi religieuse, celle de religieux extrêmistes, qui parlent très violemment lorsqu'on les contredit.

Ceci est l'effet du lavement de cervrau que la CIA leur a fait subir avec son programme MKULTRA.

Al Worden a également rejeté l'implication de la NASA dans le calcul de la trajectoire de rentrée dans la terre, s'attribuant exclusivement le mérite pour ce calcul et l'exécution de la maneuvre, ce qui contredit le rapport de mission d'Apollo 15.
Donc, entre Al Worden et l'ingénieur de la NASA qui a écrit le rapport de mission, il y en a au moins un des deux qui ment!

C'est un vrai exploit si Al Worden l'a fait, car Al Worden ne pouvait compter sur un ordinateur qui était une plaisanterie pour faire ces calculs.

Probablement qu'il a utilisé sa règle à calcul pour faire les calculs nécessaires.

Il est vrai que, même si les calculateurs au sol étaient capables de faire le travail, il était difficile pour ceux-ci de contrôler le module de commande, comme le MSFN (système de transmission de données) ne fonctionnait pas, selon la documentation technique.

Voici les tables des paramètres de rentrée pour les diverses missions.
Un premier indice que certains paramètres manquent pour certaines missions, alors qu'ils sont disponibles pour les autres missions.
Pourquoi?
Mais ce n'est pas le principal indice.

L'angle de rentrée, "flight path angle", est l'angle sous lequel le vaisseau spatial pénétre dans l'atmosphère.
Il est évident que, plus cet angle est important, et plus le module de commande descendra rapidement.
Toutefois, cet angle ne doit pas dépasser une certaine limite, sinon la vitesse de descente serait telle qu'elle causerait une surchauffe fatale du module de commande.

g représente l'accélération de la chute du module de commande, et le g maximum la valeur maximale de cette accélération.
Tout le monde comprend que, plus un corps accélère, plus il gagne de la vitesse, et donc moins il prend de temps pour couvrir une distance donnée.
Et aussi, plus vite le module de commande tombe, et plus il chauffera et encaissera des radiations.
Et aussi, plus l'angle de rentrée est important, et plus vite le module de commande descendra.
Donc pour résumer: Angle de rentrée plus important = g maximum plus grand, durée de chute plus courte, plus de chauffe et de radiations.

Les paramètres de rentrée ne sont pas aisés à étudier lorsque directement lus dans la table. C'est pourquoi je les ai représentés sous la forme de graphes superposés.
Pour chaque graphe, l'ordonnée la plus basse correspond à la valeur minimale du paramètre, et l'ordonnée la plus élevée à la valeur maximale du paramètre.
L'axe horizontal correspond aux missions Apollo 11 (sur la gauche) à Apollo 17 (sur la droite).

La mission Apollo 13, correspondant à la barre bleue représentée, est particulièrement intéressante:
Elle a un plus petit angle de rentrée que dans les missions précédentes, mais elle a une durée plus petite, ce qui est illogique, car cet angle de rentrée plus petit aurait du faire descendre le module de commande plus lentement que dans les autres missions.

Et, si nous comparons Apollo 11 (sur la gauche des graphes) avec Apollo 17 (sur la droite des graphes), nous voyons qu'Apollo 17 a une durée substantiellement plus petite que pour Apollo 11, ce qui signifie qu'il est descendu plus rapidement, des paramètres de chauffe plus élevés, ainsi qu'une dose de radiation plus élevée, ce qui est compatible avec une descente plus rapide.
Mais, alors que nous nous attendrions à ce qu'Apollo 17 ait un g maximum plus élevé que celui d'Apollo 11, il a illogiquement un g maximum un peu plus petit!
On peut trouver d'autres incohérences dans cette table, ce qui jette un sérieux doute sur ces rentrées.

Dans la section des anomalies du rapport de mission d'Apollo 12, il est dit:
"Durant l'inspection d'après vol du pont supérieur, il fut constaté que la lanière qui retient le cable électrique du bouclier thermique avant avait été sectionnée, et seulement 18 pouces de la lanière d'approximativement 45 pouces restaient."
Imaginez si la même chose étaient arrivée aux cordes du parachute.

Ceci est une animation que j'ai faite avec le module de commande tombant dans l'océan dans la mission Apollo 11.
Le module de commande flotte initialement sur ses flotteurs, ce qui est normal.
Mais, étrangement, il se retourne ensuite, et, quoique ses flotteurs soient maintenant en haut, et hors de l'eau, il s'enfonce à peine dans l'eau, comme s'il avait une structure très légère.

Et les "astronautes" qui en sont extraits, ne ressemblent guère à des humains, et font plutôt penser à des mannequins.

Site hosted by Angelfire.com: Build your free website today!