In order to land on the moon, the LM decreases a little its orbital speed (of around 75 feet/s) to take a transfer orbit which allows to bring the LM on a lower orbit.
According to the mission report of Apollo 17, the LM of Apollo 17 would reach the lower orbit, on the pericythion of the transfer orbit, at an altitude of 6.2 miles.
I initially assumed that the LM initiated its powered descent as soon as it reached the lower orbit, which means that it would then start the powered descent at an altitude of 6.2 nautical miles; 6.2 miles is equivalent to 38274 feet.
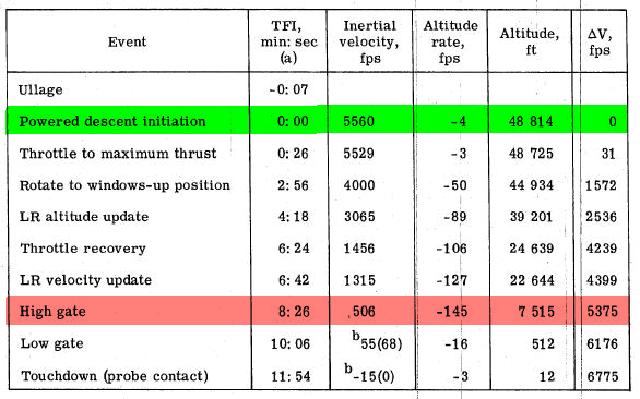
But according to the powered descent of Apollo 11, this altitude would not even represent the braking phase of the powered descent of Apollo 11.
The braking phase is the phase during which the LM reduces its very important orbital speed, without caring about its vertical speed which remains small during this phase.
The altitude lost in the braking phase is the difference between the altitude of the beginning of the powered descent and the altitude of the High Gate Event, which ends the braking phase, and this difference is equal to 41299 feet.
So, if the LM of Apollo 17 was starting its powered descent at an altitude of 38274 feet, it could not even end the braking phase.
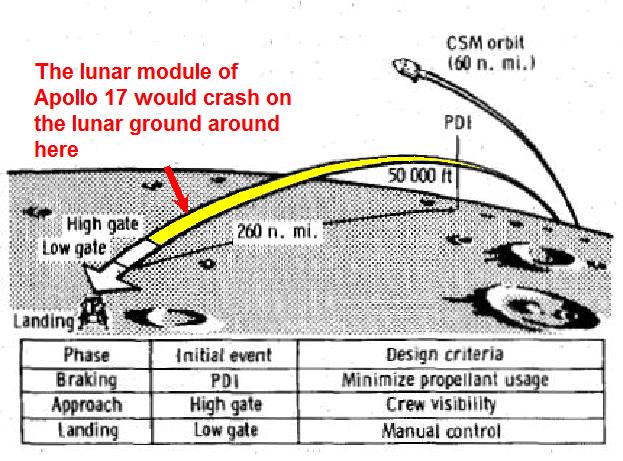
It would crash on the lunar ground a little before the end of the braking phase, with both quite important horizontal and vertical speeds.
And there is no possibility for the LM of Apollo 17 to make this braking phase shorter, for it is a little heavier than the LM of Apollo 11, but has the same engine, which means that it has more difficulty to reduce its horizontal speed than the LM of Apollo 11.
The conclusion is that, if the LM was starting its powered descent as soon as it reaches the lower orbit, at an altitude of 6.2 miles, it would be sure to crash on the lunar ground.

But the table of the trajectory parameters (3-III) indicates that the LM started in fact its powered descent at an altitude of 8.7 miles and not 6.2 miles.
8.7 miles is equivalent to to 53708 feet, so is higher than the 48814 feet of the powered descent of Apollo 11.
It is apparently sufficient to make the powered descent (unlike the 6.2 miles).

The table of trajectory parameters informs us on the moon coordinates of the point the DOI was made.
There are coordinates for the start and the end of the DOI.

The end of the DOI corresponds with the moment that the LM is on the apocynthion of the transfer orbit, so the coordinates of the apocynthion of the transfer are those of the DOI's end, so 19.2° Latitude South, and 166.77° Longitude West.
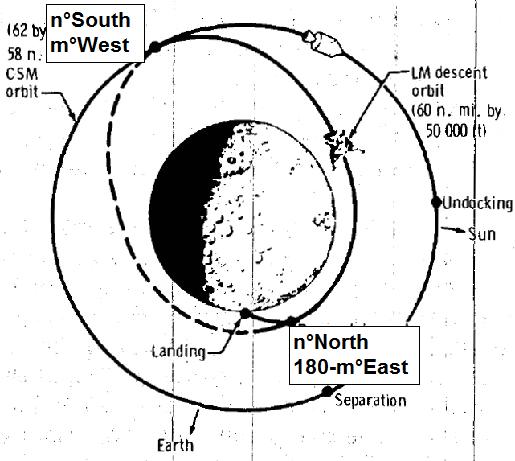
The pericynthion of the transfer orbit, which is the point that the LM reaches the lower orbit, is diametrically opposed to the apocynthion, and its moon coordinates are symmetrical to those of the apocynthion; the latitude of the pericynthion is the same as for the apocynthion, but relative to the opposite pole (i.e. North become South, and vice versa); in what concerns the longitude, the longitude of the pericynthion is the complement to 180° of the longitude of the apocynthion, and relative to the other direction (i.e. West becomes East, and vice versa).
For instance, if the moon coordinates of the apocynthion are n° Latitude South and m° Longitude West, the moon coordinates of the pericynthion are n° Latitude North and 180-m° Longitude East.
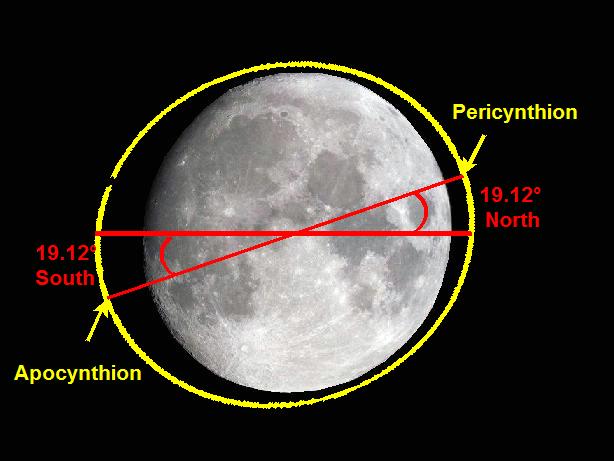
So, the latitude 19.12° South of the apocynthion of the transfer orbit becomes 19.12° North at the pericynthion of this orbit.
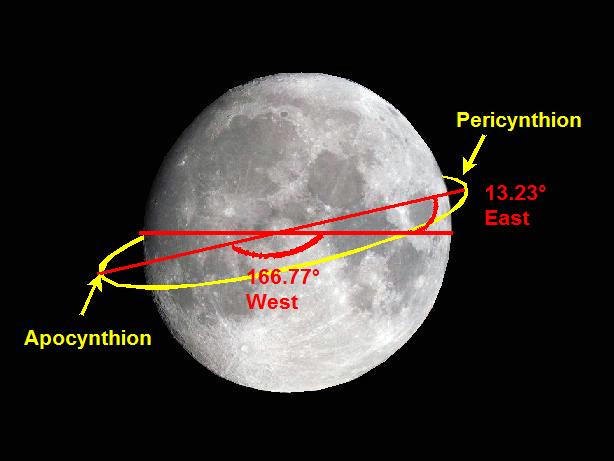
And the longitude 166.77° West of the Apocynthion becomes 180-166.77=13.23° East at the pericynthion of this orbit.
So, by the knowledge of the coordinates of the apocynthion (19.2° South, 166.77° West), we know the coordinates of the pericyntion of the transfer orbit (19.2° North, 13.23° East).

The Trajectory parameters also informs us on the moon coordinates of the point that the LM started its powered descent; they are 19.13° Latitude North and 48.75° Longitude East.
So, the point that the LM reached the lower orbit, and the point it started its powered descent, have very different longitudes (13.23° East and 48.75° East), but the same latitude or almost (only 0.01 ° difference).
The LM started its PDI with a difference of longitude of 35° before it reached the pericynthion.
I first thought that it was impossible that the PDI could have the same latitude.
However, I reasoned like only the axis apocynthion-pericynthion was making an angle with the horizontal plane of the moon, and the perpendicular axis was in the moon's horizontal plane.
The problem is that the perpendicular axis could also make an angle with the moon's horizontal plane, nothing guarantees that it is in the horizontal plane of the moon.

I chekched in the mission report of Apollo 17 if it could be confirmed that the minor axis of the transfer orbit was in the horizontal plane of the moon, but I must confess that I found nothing.
I was hoping to find a statement like: "After having a quarter of a turn around the moon, we could see the moon's equator", but, unfortunately, I found nothing such, nothing which could allow me to prove that the fact that the PDI and the pericynthion had identical latitudes was abnormal.

I could always say that it would be some coincidence if the PDI and the pericynthion had the same latitude, but the Apollo believers will tell me, and with reason, that I must prove that this coincidence cannot happen, and I must admit that I can't.

So, I remained puzzled.
Obviously the fakers meant something with identical latitudes for the PDI and the pericynthion, but in the same time they gave me no way to formally prove an anomaly.
What does that mean?

And finally the light came.
And if, instead of being intended as an anomaly, the identity of the latitudes of the PDI and the pericynthion was intended as a clue allowing to prove another anomaly?
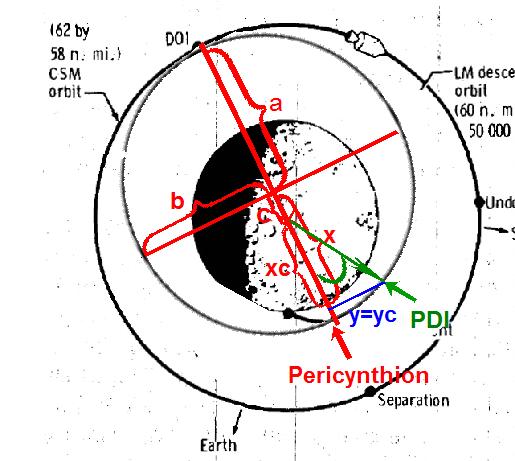
Indeed, what does the fact that the PDI and the pericynthion have the same latitude mean?
It means that the difference of longitude between the two also represents the angle between the PDI and the pericynthion (the angle represented in green on the schema) relatively to the moon's center in the reference system of the transfer orbit, which would not be the case if they had different latitudes!
If I call "Angle" this difference of longitude (equal to 35.52°), and xc and yc the coordinates of the PDI in the reference system of the transfer orbit relatively to the moon's center, we have the relationship: yc/xc=tan(Angle).
If I call x,and y the coordinates of the PDI relatively the ellipse's center, a the the semi-major axis of the ellipse, b its semi-minor axis, and c the distance between the ellipse's center and one of its foci, thus the distance between the ellipse's center of the moon's center, since the moon's center is one of its foci, we have the well known relationship:
x²/a²+y²/b²=1.
But we also have: x=xc+c, and y=yc.
So, if we use the coordinates of the PDI relatively to the moon's center, we obtain: (xc+c)²/a²+yc²/b²=1.
But we also have: xc=yc/tan(angle), which allows to replace xc in the formula which becomes:
(yc/tan(angle)+c)²/a²+yc²/b²=1.
And what do be finally obtain?
An equation of the second degree in yc, and I suppose that most of you know how to solve a such equation.
Of course, we need to know the parameters a, b and c of the ellipse, but they are easy to obtain.
First we have: 2*a=2*moon radius+altitude of Apocynthion+altitude of pericynthion.
According to the apollo 17 mission report, the altitude of the apocynthion is 59.6 nautical miles, which gives 110379 meters, and the altitude of the pericynthion is 6.2 miles, which gives 11482 meters, and the radius of the moon is 1731km.
It finally gives: a=1791930 meters.
c can be obtained with: c=a-moon radius-altitude of pericynthion, which gives c=49448 meters.
And, as there is the relationship: a²-b²=c², we can calculate b with the formula:b=square root(a²-c²), which gives b=1791247 meters.
We now have all we need to calculate the coefficients of the equation of the second degree in yc, and solving this equation gives:
yc=1017443 meters.
We can obtain xc with: xc=yc/tan(angle), which gives xc=1425351 meters with the angle of 35.52°.
And, knowing xc andf yc, we can calculate the distance of the PDI to the center of the moon with the formula: Distance=square root(xc²+yc²); after having subtracted the moon radius from this distance, we finally obtain the altitude of the PDI: Altitude of PDI=20233 meters; converted in nautical miles, it gives 10.92 nautical miles.

But, in the trajectory parameters of the mission, they tell us that the altitude of the PDI was 8.7 miles
8.7 miles instead of 10.92 miles; that makes more than two miles difference (2.22), more than 4 km!
Now we have our anomaly, and it could be proven thanks to the fact that the PDI and the pericynthion of the transfer orbit had the same latitude!
So, if the fact that the PDI and the pericyntion have the same latitude is not a proven anomaly, it allows to prove a real anomaly on the other hand!

Now, the Apollo believers still have a hope; it is a known fact that the center of the mass of the moon is a little different from its geometrical center; there would be a distance of several kilometers between them; this distance is generally considered equal to 2 kilometers, but it may be a little more.
The center of mass is closer to the earth than the geometrical center, so closer to the pericynthion of the transfer orbit.
It means that the distance between the center of the ellipse and one of its foci is increased by the distance between the two centers, since the center of mass is the real focus of the ellipse; the consequence is that the semi-minor axis is a little smaller (since we have the relationship: b²=a²-c²), and the transfer orbit a little flatter; this of course is going to reduce a little the altitude of the PDI.

What I have said opens of course a window of hope for the Apollo believers.
Is the altitude of the PDI going to be reduced enough to match with the altitude indicated on the trajectory parameters?

I am going to be generous; the generally accepted distance between the two centers is 2 kilometers, but, if I take that distance, the Apollo believers will tell me: You are not sure that this distance is the exact distance, it might be a little more.
That's why I am going to take consistently more; I am going to take 10 kilometers for this distance, five times more than the accepted distance.
This way, I am sure that the distance I take will not be smaller than the real distance between the two centers.
And now let's do all the calculations again, this time taking into account the (exaggerated) distance between the two centers of the moon.
The distance between the ellipse's center and its focus becomes: distance between ellipse's center and geometrical center + (exaggerated) distance between centers=59448 meters.
If I call c' the distance between the ellipse's center and the center of mass, we have the relationship: b²=a²-c'², which gives b=1790944 meters.
After having recalculated the coefficients of the equation of the second degree, and having solved it, we find: yc=1017386 meters.
This allows us to calculate the new value of xc: xc=1425271 meters.
After having calculated the distance to the (geometrical) center of the moon, and subtracted the moon's radius, we finally obtain the new altitude of the PDI: 20135 meters; in miles, it gives 10.87 nautical miles.
So, by taking into account the distance between the two centers of the moon, and largely exaggerating it, we have only gained 0.05 miles, not even a tenth of a mile, when we needed to gain 2.22 miles to erase the anomaly.
We can call that death of a deceived hope!

