Exponential Functions

An Exponential Function is a way to depict a growth or decay

y = ab^x

a is a constant and does not equal 0

b is the base and cannot equal 1

x is a real number

y = 4(2)^x y = 3(2)^x y = 2(2)^x y = 1(2)^x

On this graph, you can see that the a value affects the point on the Y-axis that the graph hits.

If a were to equal zero, the equation would be y=0 which isn't an exponential graph.

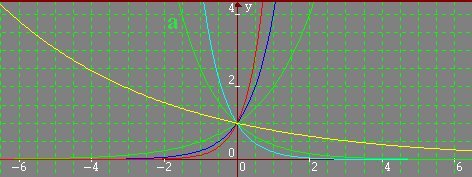
y = 1(.8)^x [a] y = 1(.4)^x y = 1(.2) y = 1(2)^x y = 1(4)^x y = 1(8)^x

When b > 1, the graph represents a growth, and b is the Growth Factor (the rate of growth)

However, when b < 1, the graph represents a decay, and likewise the b is the Decay Factor (the rate of decay)

If b were to equal zero, the graph would neither be growing nor decaying, and be a straight line, which isn't an exponential graph.