swings

Site hosted by Angelfire.com: Build your free website today!

Amusement Park Physics: Swings

Objectives:

1. Students will be able to understand Centripetal Acceleration
2. Calculate Centripetal Acceleration
3. Describe Centripetal Forces

Real Life Applications:

Swings are used everyday in Amusement parks and enjoyed by everyone. Acceleration needs to be calculated to make sure the ride remains safe and workable.
A thether ball game also works the same way as a swing. If the ball goes too fast, it can hurt someone. This game is played a lot by elementary school students and many do not know the physics of this game.

Concepts:

Centripetal Acceleration is a physics principal used by swings. Acceleration is descirbed as either a change in speed or direction. A swing is constantly changing direction, so it is therefore accelerating. In one of Newton's Laws it states all accelerations are created by forces that act upon the object. Centripetal accelerations use this Law because the forces accelerating the swings are acting toward the center of the circle formed by a circular path. The forces creating the acceleration are known as Centripetal Forces. The actual Centripetal Forces are the tension forces on the rope/chain connecting to the ride.

The magnitude of the Centripetal Acceleration (A_c) is calculated by :

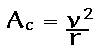
Where v is the speed of object(m/s) and r is the radius of the circle(m).

The magnitude of the Centripetal Force (F_c) is calculated by:

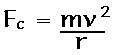
Where m is mass(kg), v is the speed of the object(m/s), and r is the radius of the circle(m).

Examples:

1. A swing at Busch Gardens has a diameter of 40 meters and a velocity of 25 m/s. Find the Centripetal acceleration of the swing using the above equation.

A_c= v² A_c= (25 m/s)² A_c= 15.625 m/s²
^{r

40 m}

2. The force of the swing on the riders is different for every one. Calculate the force upon a 58.5 kg women who is going 45 m/s. The swing has a radius of 25 meters.

F_c= mv² F_c= (58.5 kg)(45 m/s)² F_c= 4738.5 N
^{r

25 m}

3. Centripetal forces on a swing at Disney World need to be calculated in order for the ride to function properly. The acceration of the ride is 19.37 m/s² and the average mass of the passengers is 64.3 kg. Calculate the centripetal force of the swing.

F_c= mv² since acceleration= v² F_c= ma F_c= (64.3kg)(19.37 m/s²) F_c= 1245.491 N
^{r

r}

Links:

Diagrams:
http://library.thinkquest.org/2745/data/centrip3.htm

Centripetal Force:
http://library.thinkquest.org/C005075F/English_Version/swings.htm