Algebra Boolean

Komputer dibina menggunakan litar elektronik digit yang pantas. Litar sedemikian boleh dibahagikan kepada dua jenis iaitu diskret dan bersepadu. Komponen diskret mempunyai cuma satu peranti contohnya perintang, pemuat atau diod. Litar bersepadu (IC) pula mengandungi komponen-komponen yang banyak di dalamnya. Penggunaan IC membolehkan sistem dibina dengan lebih kecil dan lebih padat. Pereka bentuk tidak perlu memahami secara terperinci kendalian litar dalaman sesuatu IC untuk menggunakannya dengan berkesan. Dengan litar digit kita lebih mementingkan fungsi logik litar tersebut dan bukan ciri elektriknya. Bagaimanapun, kita mesti mematuhi peraturan asas tentang bekalan kuasa dan keperluan masukan dan keluaran litar tersebut.

Litar Logik

Litar bersepadu dibina dari litar asas dinamai get. Penyambungan get dinyatakan secara matematik melalui logik perduaan.

Logik Perduaan

Litar logik digit mengendalikan pemboleh ubah yang hanya boleh mempunyai dua nilai. Dua nilai ini boleh diberikan berbagai-bagai nama (seperti benar dan palsu, ya dan tidak, dan sebagainya), tetapi untuk memudahkan perbincangan kita berikan nilai-nilai 0 dan 1. Logik perduaan digunakan untuk menyatakan olahan maklumat perduaan menggunakan matematik. Cabang matematik khusus bagi mengolah nilai-nilai perudaan ini dinamakan aljabar Boolean.

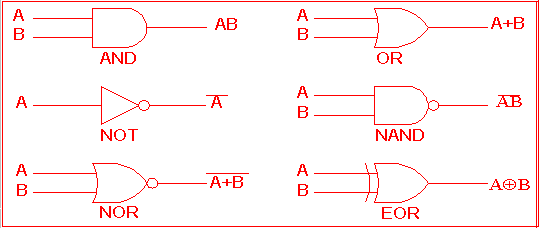
Logik perduaan terdiri dari pemboleh ubah dan kendalian. Pemboleh ubah boleh dinyatakan dengan huruf-huruf seperti A, B, C, P, Q, X, Y, Z dan sebagainya. Terdapat tiga kendalian utama iaitu AND, OR dan NOT.

Kendalian AND

AND Gate

A	B	Q
0	0	0
0	1	0
1	0	0
1	1	1

AND Gate

A	B	Q
0	0	0	If A is 0 AND B is 0, Q is 0.
0	1	0	If A is 0 AND B is 1, Q is 0.
1	0	0	If A is 1 AND B is 0, Q is 0.
1	1	1	If A is 1 AND B is 1, Q is 1.

Kendalian AND dinyatakan dengan tanda titik atau dengan ketiadaan pengendali. Umpamanya,

atau Q = AB

dibaca Q bersamaaan A AND B. Pemboleh ubah Q hanya boleh bernilai 1 jika A dan B bernilai 1. Pada ketika-ketika lain, Q bernilai 0.

Kendalian OR

OR Gate

A	B	Q
0	0	0
0	1	1
1	0	1
1	1	1

Kendalian OR dinyatakan dengan tanda campur.

Umpamanya,

Q = A + B

dibaca Q bersamaaan A OR B. Pemboleh ubah Y boleh bernilai 1 jika A atau B bernilai 1. Sekiranya A dan B bernilai 0, Q bernilai 0.

Kendalian NOT

NOT Gate

A	Q
0	1
1	0

Kendalian NOT dinyatakan dengan tanda bar. Umpamanya,

dibaca Q tidak bersamaaan A. Ini bermaksud Q mempunyai nilai yang bertentangan dengan A. Jika A bersamaan 0 , Q bernilai 1, tetapi jika X bersamaan 1, Q bernilai 0.

Kendalian-kendalian Lain

Kendalian NOR

NOR Gate

A	B	Q
0	0	1
0	1	0
1	0	0
1	1	0

Kendalian NOR dinyatakan dengan tanda campur dan tanda bar.

Umpamanya,

Pemboleh ubah Q hanya boleh bernilai 0 jika salah satu dari A dan B bernilai 1. Ini bermaksud ia menghasilkan 1 apabila kesemua masukannya 0.

Kendalian NAND

NAND Gate

A	B	Q
0	0	1
0	1	1
1	0	1
1	1	0

Umpamanya,

Pemboleh ubah Q hanya boleh bernilai 0 jika kedua-dua A dan B bernilai 1. Pada ketika-ketika yang lain Q bernilai 1.

Kendalian XOR

XOR Gate

A	B	Q
0	0	0
0	1	1
1	0	1
1	1	0

Kendalian XOR dinyatakan dengan bulatan bertanda campur.

Umpamanya,

Pemboleh ubah Q hanya boleh bernilai 1 jika jumlah masukan yang bernilai 1 adakah ganjil. Ini bermaksud ia menghasilkan 0 apabila kesemua masukannya 0 atau 1.