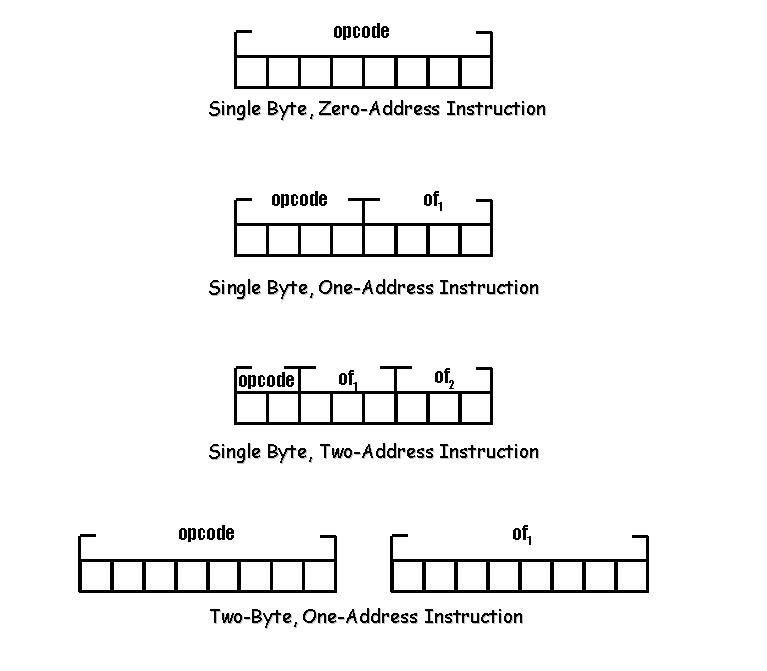
Instruction Format - defines the layout of the bits of an instruction in terms of its constituent parts. The layout of a computer instruction is a sequence of bits.

The format divides the instruction into fields, corresponding to the constituent parts of an instruction (e.g. opcode, operand). The format must implicitly or explicitly indicate the addressing mode for the operand.

Operation Code (OpCode)

a code used to represent the operations of a computer.

Operands

that which is operated on. This is usually identified by an address part of an instruction.

Implicit

the opcode alone provides the CPU with adequate information for the required action. i.e. An instruction to halt CPU operation need not anything more than an opcode.

Explicit

is referenced by using one of the different addressing modes.

NOTE: For most instruction sets, more than one instruction format is used.

SOME INSTRUCTION FORMATS OF THE INTEL 8085

1. Instruction Length

   The most basic design issue to be faced is the instruction format length. Instruction lengths vary from one to many bytes. The length of an instruction depends on:

   • the number of operands it involves, and,
   • the way it specifies each operand

   This decision affects, and is affected by the following:

   • memory size
   • memory organization
   • bus instruction
   • CPU complexity
   • CPU speed

   This decision determines the richness and flexibility of the machine, as seen by the assembly language programmer. Programmers want:

   • More OpCodes and Operands - make life simpler for the programmer, since shorter programs can be written to accomplish given tasks.
   • Greater Addressing Range - this gives the programmer greater flexibility in implementing certain functions, such as table manipulation and multiple-way branching.
   • Greater Addressing Range - due to the size of the main memory and the increasing use of virtual memory.

   All of these things (opcodes, operands, addressing modes and addressing range) require bits and push in the direction of longer instruction lengths. But longer instructions may be wasteful. A 32-bit instruction occupies twice the space of a 16-bit instruction, but is probably less than twice as useful.

   Beyond this basic trade off, there are other considerations like:

   • Instruction Length = Memory Transfer Length in a bus system or should be a multiple of the other. Otherwise, we will not get an integral number of instructions during the fetch cycle.
   • Memory Transfer Rate has not kept up with the increases in processing speed.
   • Memory can become a bottleneck , that is, the processor can execute instructions faster that it can handle them.

   There are solutions provided for such considerations or problems:

   • Use of Cache Memory - a memory that is smaller and faster than the main memory and that is interposed between the CPU and the main memory. The cache acts as a buffer for recently used memory locations.
   • Use of Shorter Instructions - 16-bit instructions can be fetched at twice the rate of 32-bit instructions, but probably can be executed less than twice as fast.
   • Instruction Length Should Be a Multiple of the Character Length - is usually 8 bits and of the length of fixed-point numbers.

   The word length of memory is, in some sense, the "natural" unit of organization. The size of the word usually determines the size of the fixed-point numbers, wherein usually the two are equal. Word size is also typically equal to, or at least integrally related to the memory transfer size. Since a common form of data is character data, we would like a word to store in integral number of characters. Otherwise there will be wasted bits in each word when storing multiple characters, or character will have to straddle a word boundary.

   Example: REGISTERS BASICALLY STORE 1 BIT

   The opcode field of an 8-bit µP is fixed to 8 bits. Two address instruction employ a second byte that accumulates two 4-bit long operand fields. What is the total number of available opcodes? Up to how many registers can we encode in each operand field?

   Solution

   # of OpCodes = 2 ⁿ = 2 ⁸ = 256 OpCodes

   # of Registers = 2 ⁿ = 2 ⁴ = 16 Registers
   
   

2. Allocation of Bits

   An equally difficult issue is that of how to allocate bits in the specified format. For a given instruction length, there is clearly a trade off between the number of opcodes and the power of addressing.

   The following interrelated factors go into determining the use of addressing bits:

   • Number of Addressing Modes
   • Number of Operands
   • Register V.S. Memory
   • Number of Register Sets
   • Addressing Range
   • Address Granularity
   
   
   
3. Variable Length Instructions

   This tactic makes it easy to prove a large repertoire of opcodes, with different opcode lengths. Addressing can be more flexible, with various combinations of register and memory references plus addressing modes. With variable length instructions, opcodes can be provided efficiently and compactly.

   The principal price to pay for variable length instructions is an increase in the complexity of the CPU. Falling hardware prices, the use of microprogramming, and a general increase in understanding the principles of CPU design have all contributed to making this a small price to pay.

   The use of variable length instructions does not remove the desirability of making all of the instruction lengths integrally related to the word length. Since the CPU does not know how the length of the next instruction is to be fetched, a typical strategy is to fetch a number of bytes or words equal to at least the longest possible instruction. This is a good strategy to follow in any case.

   Example:

   The operand field expands into what is ordinarily operand field 2. Up to how many additional opcodes can we economize by doing so? Could we economize even more? What are the trade-offs?

   Solution:

   Additional OpCodes = 2 ⁿ = 2 ⁵ = 32 Additional OpCodes

   Trade-offs - (if all 0s) This will provide 32 opcodes. Extra opcodes would be gained at the expense of prog-flexibility because OF₂ is not allowed to specify register.