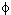 (n), the number of integers k with 1
(n), the number of integers k with 1 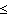 k
k 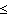 n and k coprime to n. He proved another of Fermat's assertions, namely that if a and b are coprime then a2 + b2 has no divisor of the form 4n+1, in 1749.
n and k coprime to n. He proved another of Fermat's assertions, namely that if a and b are coprime then a2 + b2 has no divisor of the form 4n+1, in 1749.
Perhaps the result that brought Euler the most fame in his young days was his solution of what had become known as the Basel problem. This was to find a closed form for the sum of the infinite series  (2) =
(2) =  (1/n2), a problem which had defeated many of the top mathematicians including Jacob Bernoulli, Johann Bernoulli and Daniel Bernoulli. The problem had also been studied unsuccessfully by Leibniz, Stirling, de Moivre and others. Euler showed in 1735 that
(1/n2), a problem which had defeated many of the top mathematicians including Jacob Bernoulli, Johann Bernoulli and Daniel Bernoulli. The problem had also been studied unsuccessfully by Leibniz, Stirling, de Moivre and others. Euler showed in 1735 that  (2) =
(2) = 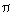 2/6 but he went on to prove much more, namely that
2/6 but he went on to prove much more, namely that  (4) =
(4) = 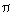 4/90,
4/90,  (6) =
(6) = 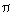 6/945,
6/945,  (8) =
(8) = 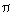 8/9450,
8/9450,  (10) =
(10) = 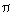 10/93555 and
10/93555 and  (12) = 691
(12) = 691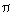 12/638512875. In 1737 he proved the connection of the zeta function with the series of prime numbers giving the famous relation
12/638512875. In 1737 he proved the connection of the zeta function with the series of prime numbers giving the famous relation
Here the sum is over all natural numbers n while the product is over all prime numbers.(s) =
(1/ns ) =
(1 - p-s)-1
By 1739 Euler had found the rational coefficients C in  (2n) = C
(2n) = C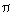 2n in terms of the Bernoulli numbers.
2n in terms of the Bernoulli numbers.
Other work done by Euler on infinite series included the introduction of his famous Euler's constant 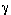 , in 1735, which he showed to be the limit of
, in 1735, which he showed to be the limit of
1/1 + 1/2 + 1/3 + ... + 1/n - loge nas n tends to infinity. He calculated the constant
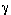 to 16 decimal places. Euler also studied Fourier series and in 1744 he was the first to express an algebraic function by such a series when he gave the result
to 16 decimal places. Euler also studied Fourier series and in 1744 he was the first to express an algebraic function by such a series when he gave the result
in a letter to Goldbach. Like most of Euler's work there was a fair time delay before the results were published; this result was not published until 1755./2 - x/2 = sin x + (sin 2x)/2 + (sin 3x)/3 + ...
Euler wrote to James Stirling on 8 June 1736 telling him about his results on summing reciprocals of powers, the harmonic series and Euler's constant and other results on series. In particular he wrote [59]:-
Concerning the summation of very slowly converging series, in the past year I have lectured to our Academy on a special method of which I have given the sums of very many series sufficiently accurately and with very little effort.He then goes on to describe what is now called the Euler-Maclaurin summation formula. Two years later Stirling replied telling Euler that Maclaurin:-
... will be publishing a book on fluxions. ... he has two theorems for summing series by means of derivatives of the terms, one of which is the self-same result that you sent me.Euler replied:-
... I have very little desire for anything to be detracted from the fame of the celebrated Mr Maclaurin since he probably came upon the same theorem for summing series before me, and consequently deserves to be named as its first discoverer. For I found that theorem about four years ago, at which time I also described its proof and application in greater detail to our Academy.Some of Euler's number theory results have been mentioned above. Further important results in number theory by Euler included his proof of Fermat's Last Theorem for the case of n = 3. Perhaps more significant than the result here was the fact that he introduced a proof involving numbers of the form a + b
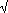 -3 for integers a and b. Although there were problems with his approach this eventually led to Kummer's major work on Fermat's Last Theorem and to the introduction of the concept of a ring.
-3 for integers a and b. Although there were problems with his approach this eventually led to Kummer's major work on Fermat's Last Theorem and to the introduction of the concept of a ring.
One could claim that mathematical analysis began with Euler. In 1748 in Introductio in analysin infinitorum Euler made ideas of Johann Bernoulli more precise in defining a function, and he stated that mathematical analysis was the study of functions. This work bases the calculus on the theory elementary functions rather than on geometric curves, as had been done previously. Also in this work Euler gave the formula
eix = cos x + i sin x.In Introductio in analysin infinitorum Euler dealt with logarithms of a variable taking only positive values although he had discovered the formula
ln(-1) =in 1727. He published his full theory of logarithms of complex numbers in 1751.i
Analytic functions of a complex variable were investigated by Euler in a number of different contexts, including the study of orthogonal trajectories and cartography. He discovered the Cauchy-Riemann equations in 1777, although d'Alembert had discovered them in 1752 while investigating hydrodynamics.
In 1755 Euler published Institutiones calculi differentialis which begins with a study of the calculus of finite differences. The work makes a thorough investigation of how differentiation behaves under substitutions.
In Institutiones calculi integralis (1768-70) Euler made a thorough investigation of integrals which can be expressed in terms of elementary functions. He also studied beta and gamma functions, which he had introduced first in 1729. Legendre called these 'Eulerian integrals of the first and second kind' respectively while they were given the names beta function and gamma function by Binet and Gauss respectively. As well as investigating double integrals, Euler considered ordinary and partial differential equations in this work.