| V.37(2001) No 3, pp. 233 - 243 |
237 - 238 |
Transformation
of divergence theorem |

|
| p. 237 Plot the
diagram of  (x,
t) space-time variation, remembering the progressive pattern of wave (7).
Basing on the diagrams of F(x, t) shown in Fig. 1,
centre, we can easy determine (x,
t) space-time variation, remembering the progressive pattern of wave (7).
Basing on the diagrams of F(x, t) shown in Fig. 1,
centre, we can easy determine 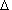  0i , since the integration amounts to a
simple multiplying of 0i , since the integration amounts to a
simple multiplying of  (x, t) parameters at a picked out
moment of time t at a studied surface into the size of this surface. The
obtained results calculated for the moments fixed in Fig. 1, left are shown in Fig. 1,
right. As we can see from calculation, despite we used the conventional definition and
method, the obtained value (x, t) parameters at a picked out
moment of time t at a studied surface into the size of this surface. The
obtained results calculated for the moments fixed in Fig. 1, left are shown in Fig. 1,
right. As we can see from calculation, despite we used the conventional definition and
method, the obtained value 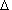  0i in general case does not
vanish at the boundaries of the picked out regions. It is different both for all the
surfaces a1, a2, a3
and all the moments of time, though 0i in general case does not
vanish at the boundaries of the picked out regions. It is different both for all the
surfaces a1, a2, a3
and all the moments of time, though 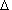  0i was calculated relatively to
the surface a0 common for all the regions and simultaneously for all
the picked out regions. The regularity 0i was calculated relatively to
the surface a0 common for all the regions and simultaneously for all
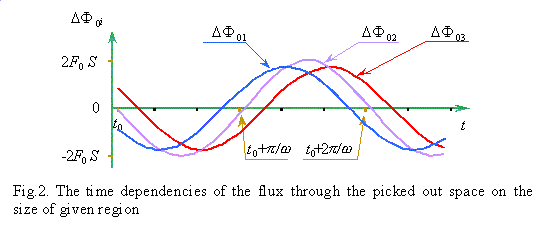
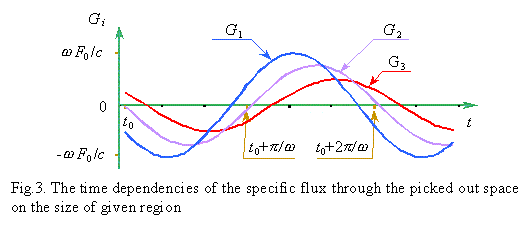
the picked out regions. The regularity 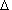  0i(t) shown in Fig. 2 reflects
this peculiarity; it is plotted on the basis of calculation of Fig.1. As we see from Fig.
2, both amplitude and phase of 0i(t) shown in Fig. 2 reflects
this peculiarity; it is plotted on the basis of calculation of Fig.1. As we see from Fig.
2, both amplitude and phase of  0i(t) are different for
the picked out regions, the same as these parameters are different for Gi(t)
whose regularity is shown in Fig. 3. The more, when diminishing the size of picked
out region, the amplitude of Gi increases. It confirms that the
flux through a picked out region is time-inconstant in dynamical fields, and the fact of 0i(t) are different for
the picked out regions, the same as these parameters are different for Gi(t)
whose regularity is shown in Fig. 3. The more, when diminishing the size of picked
out region, the amplitude of Gi increases. It confirms that the
flux through a picked out region is time-inconstant in dynamical fields, and the fact of   0i
time-variation is conditioned not by the space parameters of flux, but namely by
the progressive pattern of wave, which we can easy prove mathematically. 0i
time-variation is conditioned not by the space parameters of flux, but namely by
the progressive pattern of wave, which we can easy prove mathematically. |
|
Actually, for
any region picked out at a moment t we have |
|
(9) |
(where 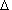 xi
= xi - x0 is the distance between the
surfaces ai and a0). Considering
that in the studied case Vi = xi
= xi - x0 is the distance between the
surfaces ai and a0). Considering
that in the studied case Vi =  xiS, we obtain (8) for Gi
as xiS, we obtain (8) for Gi
as |
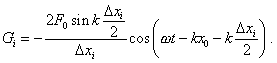
|
(10) |
Because the
regularity Gi( xi) is conditioned by the finite
velocity of the wave space-propagation, we can express xi) is conditioned by the finite
velocity of the wave space-propagation, we can express  xi through the time
characteristic of the wave delay xi through the time
characteristic of the wave delay 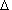 ti: ti: |
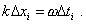
|
(11) |
p. 238
Substituting (11) into (10), we obtain
|
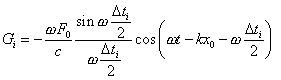
|
(12) |
(where c
is the wave propagation velocity). As we see from (12), both amplitude and phase of Gi
depend on 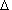 ti;
it completely corresponds to the plot shown in Fig. 3. With it the specific flux amplitude
depends on the ratio of sine of argument ti;
it completely corresponds to the plot shown in Fig. 3. With it the specific flux amplitude
depends on the ratio of sine of argument   ti/2 to this argument, determining the
first significant limit. It backgrounds that the inequality of flux to zero in dynamic
fields is the objective fact. ti/2 to this argument, determining the
first significant limit. It backgrounds that the inequality of flux to zero in dynamic
fields is the objective fact. |
|
To determine
the divergence on the basis of (12) in accord to (2), it is sufficient to find the limit
of Gi at  ti ti  0. Taking it for any of picked out regions at the
moment t, we obtain: 0. Taking it for any of picked out regions at the
moment t, we obtain: |
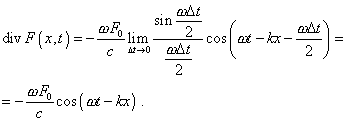
|
(13) |
Thus, similarly
to the flux, the divergence of  (x, t) does not vanish too, and
Levitch’s expression (5) in the case of 1D flux and harmonic time-dependence of
longitudinal vector (x, t) does not vanish too, and
Levitch’s expression (5) in the case of 1D flux and harmonic time-dependence of
longitudinal vector 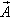 ( ( , t) will completely correspond to (13). On
one hand it corroborates the result obtained by Levitch for the vector potential of dipole
radiator, and on the other hand, it shows more general pattern of the result. , t) will completely correspond to (13). On
one hand it corroborates the result obtained by Levitch for the vector potential of dipole
radiator, and on the other hand, it shows more general pattern of the result.
So we can state
that at least for any 1D flux in dynamical fields the divergence of its vector does not
vanish, being inconsistent with the conventional concepts basing on Poisson theorem.
We should note
again, as we mentioned in the introduction, the difference between the obtained results
and conventional concept is conditioned by the fact that in all the theorems proved before
on the basis of divergence definition, in fact only stationary fields and stable fluxes
were considered. While in dynamical fields, not only the density of space-distribution of
the force lines, but also the wave propagation velocity, being finite and causing the
phase delay, have effect on the value of divergence. |