We can extend the line through the centers of the two cue balls to help us. This will help us see the approximate angle of θ, therefore letting us solve the equation for φ.
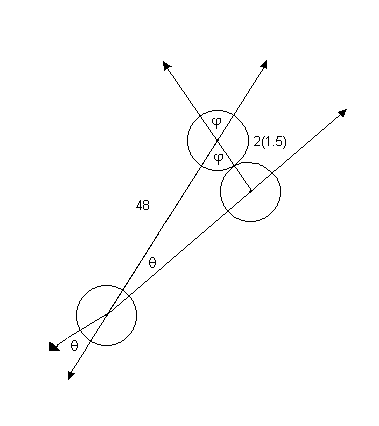
Lets say that we shoot the Cue ball at a 0.5o angle. Then we can plug 0.5o as θ in our equation.
Lets set up the problem using the equation that we found in the earlier.
Equation for finding the angle of a shot: d/2r* (sinθ) = sin(θ+φ)
Becomes: 48/ 2(1.5) * sin(0.5) = Sin(0.5+φ)
We can now simplify the left side of the equation by doing arithmetic.
Our equation: 48/ 2(1.5) * sin(0.5) = Sin(0.5+φ)
Simplifying 48/2(1.5): 16*sin(0.5) = sin(0.5+φ)
Now we can find the value of sin(0.5) and substitute that in our equation.
Our equation: 16*sin(0.5) = sin(0.5+φ)
Simplifying sin(30): 16 * 0.00873 = sin(0.5+φ)