Because vertical angles are congruent, we can place φ in the angle below.
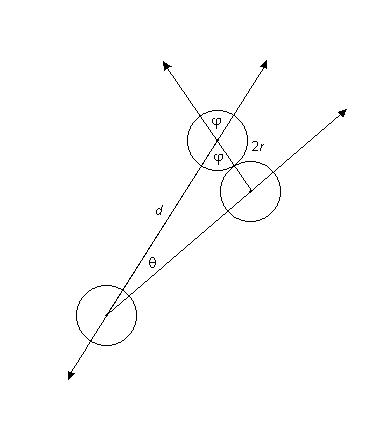
By drawing these lines we have set up triangles. We can now put the angles and the distances into the Law Of Sines.
Law of Sines: (sin A)/a = (sin B)/b
Our Equation: (sin θ) /2r = sin[180-(θ+φ)]/d
The numerator on the left side of the equation comes from our triangle. Since all angles in a triangle must add up to 180, you can subtract θ and φ from 180 to get the measure of the unknown angle. (Click here for an further explanation)
We can multiply both sides by d so that we can get d out of the denominator on the left side.
Equation: sinθ/ 2r = sin[180-(θ+φ)]/d
Multiply by d: x d = x d
You get: d/2r sinθ= sin[180-(θ+φ)]
Now we can put this formula in the Sine Addition Formula.
Law of Sine Addition: sin(a+b)=sina cosb + sinb cosa
Equation: d/2r * sinθ=sin(180)cos(-(θ+φ))-sin(-(θ+φ))cos(180)
Plugging in sin(180) into our calculators we can see that it equals 0. This makes our equation change. We are able to completely expel the first half of the equation on the left side because anything multiplied by 0 becomes 0.
Equation: d/2r*sinθ= sin(180)cos(-(θ+φ))-sin(-(θ+φ))cos(180)
Becomes: d/2r*sinθ= -sin(θ+φ)cos(180)