"How high was my plane in this photograph?"
The most common question in model related aerial photography...
Here's a fairly simple way to find out, and plan for a photo shoot.
The starting point is to determine the field of view (fov) of the camera.
To do this, set up a object of a known dimension, a known distance from the camera, and photograph it.
A 4 foot carpenters scale set at 10 feet from the camera, at the same level as the camera is a
reasonable
selection.. The longer the object is, the more precise the fov computation will be.
Extreme distance to a large object isn't needed.

Using the object dimension and distance to it in an uncropped image, the camera fov
is found by measuring the length of the known dimension
in pixels, and finding the actual width of the fov...
In the image, the 48" scale is 675 pixels long.
The width of the image edge-to-edge is 1280 pixels.
The ratio of the known distance to the image width is 1.89, so the image width at the plane of the
object is 1.89 times 48 inches, or 91 inches across.
With the camera at 120 inches from the scale, compute the angle of one half the field view width in
inches..

45.5 inches divided by 120 inches is .3791.. this is the tangent of the angle from the center of the
image to one side. Taking the arc-tangent of that gives one half the fov angle, or 20.7 degrees. The full
fov is then 41.4 degrees on the long side of the image.
For this lens, labeled as 7mm focal length, it's equivalent to a 50 mm lens in the 35 mm film format.
Now for a typical aerial photograph of an object of known length, the distance from that object can
be determined.
When the camera is directly over the object, looking straight down, the distance from camera to
object will be the altitude of the camera.
For the more usual oblique image, the distance will not be the altitude, which can be determined
using more measurements.
 In this image, the asphalt taxiway is known to be 400 feet long.
Measuring the length of the taxiway in pixels and ratioing that to the image width at that location
on the image gives us the width of the image. Halving that width, and using the 1/2 angle tangent equation..
The side opposite divided by the tangent of the half fov angle gives the distance from the
center of the taxiway to the camera.
In this image, the asphalt taxiway is known to be 400 feet long.
Measuring the length of the taxiway in pixels and ratioing that to the image width at that location
on the image gives us the width of the image. Halving that width, and using the 1/2 angle tangent equation..
The side opposite divided by the tangent of the half fov angle gives the distance from the
center of the taxiway to the camera.

This gives a distance from the taxiway to the camera of 1055 feet.
To determine the altitude of the plane:
The image widths at the bottom and top of the image are used; any two known locations can be used.
Since the ground is flat, it's permissible to extend the sides of the taxiway to the bottom
and top of the image, following the perspective of these sides in the image to the upper and lower
edges of the image.
By using the process above, finding the image width in feet at the edges of the image and the
location of the camera where these two distances intersect in space is the plane's location.

...Nifty way to get altitude....
Taking the fov angular and distance to the image edges into a CAD program, the plane's
altitude can be found...
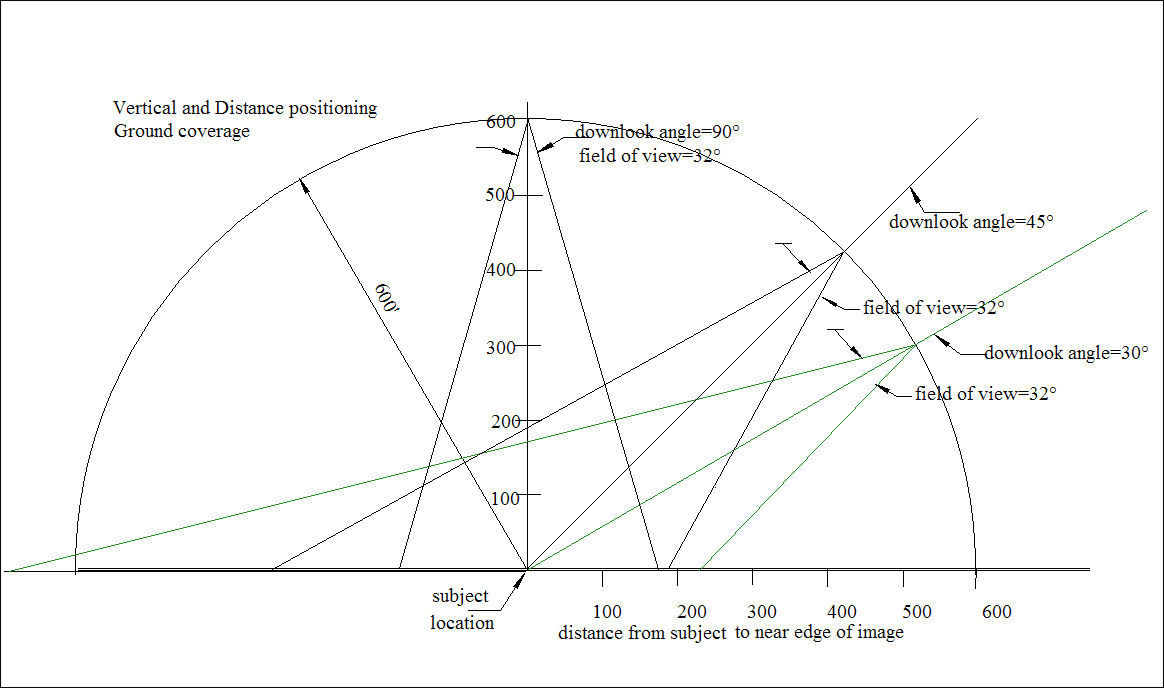
For the typical horizontal image layout:
1) Lay out the camera field of view in degrees..
2) For the distance from the camera to the upper edge of the image, lay out that length.. to scale,
if necessary.
3) From the vertex of the fov angle, lay out the distance to the lower edge of the image as a
radius at the same scale along the lower side of the field of view angle.
Where this radius crosses the lower edge of the fov determines the intersection with the ground.
Connecting the two ground intersections gives the ground location, relative to the camera look-down
angle. The drawing can be rotated to put the ground line horizontal.
Extending this line past the fov vertex gives a reference for altitude.
A perpendicular from the ground line to the fov vertex is the altitude at the drawing scale used.

...Mathy way to get altitude....
From the computations or the drawing, there's three values that can be use to derive the other distances and angles
which can be used to find altitude.. It's the classic SAS of trig..
Side.. the distance from the camera
to the lower edge of the image...
Angle, the field of view, and
Side, the distance from the camera
to the upper edge of the image.
First, the ground distance between the lower and upper image points..

The Law of Cosines works here:
...........side c²=side a²+side b²-2*side a*side b(cos c)....:
Where a is the distance from the camera to the lower edge of the image...
Where b is the distance from the camera to the upper edge of the image...
Where c is the camera field of view for the short axis of the image...
....Ground distance in the image=√(1995²+828²-2*1993*828*cos(32)) =1365 feet
This gives us the SSS values for the triangle, from which the missing two angles and then the
altitude can be determined:
....To determine the altitude of the camera...
The Law of Sines:
sin a/ side
a= sin b/side b= sin c/side c
Using the sides previously computed:
The angle the upper limit of the field of view makes with the ground is:
sin a/ side a= sin c/side c
... sin a= 828*sin 32/1365= 19.8°
With two of the interior angles, the third is the sum of the two subtracted from 180°..which
is the third interior angle, or 128°. The angle from the ground to the camera at the lower edge
of the image is 180°-128°, or 51.8°.
The altitude then is the distance from the camera to the lower edge of the image times the sine
of 51.8°, which is 650 feet, agreeing with the graphical solution in the CAD drawing.
To perform preflight planning of a photo expedition:
A simple rule of thumb is to look at the tangent of the total fov angle, and divide that into the length of
the subject.
The resultant number is the distance the camera must be from the longest dimension of the object
of interest in the photo to get it all of it into the photo.

Then the downlook angle, either set with the camera in the plane, or by some other means, to get the
desired view of the subject...
Photogrammetry 101
Paul J. Burke May 5, 2006
..Return to Main Menu..
E-mail to: Paul J. Burke








