Site hosted by Angelfire.com: Build your free website today!

 

Mathematics 5

Review Worksheet 4


1.
A tower stands on top of a hill.  From a point on level ground, the angle of eleveation to the top of the tower is 18°.
From a point 250 m closer to the hill, the angle of elevation to the top of the tower is 23°, and the angle of elevation to the bottom of the tower is 20°.
How tall is the tower?

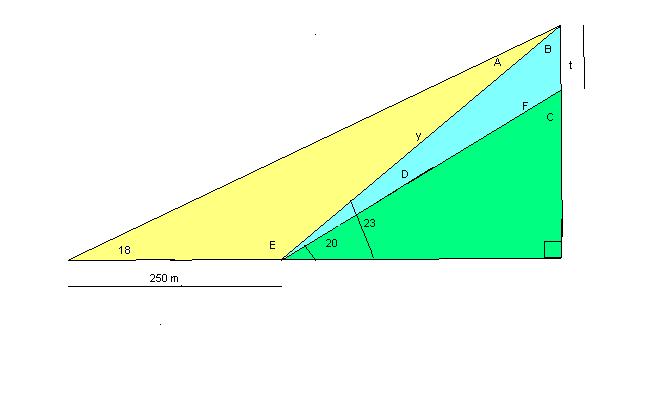
By using the sum of angles of a triangle theorem (SATT),  and the fact that a line = 180°,  the following can be determined:
C = 70° (Green triangle)
F = 110°
D = 3°
B = 67°
E = 157°
A = 5°

In the yellow triangle, the sine law gives us :
250/sin5 = y/sin18
y = 886.4

In the blue triangle, the sine law gives us:
886.4/sin 110 = t/sin3
t = 49.3

therefore, the height of the tower is 49.3m.
 


2.
Fill in the chart.  Do not use a calculator.  You may use a pencil and paper.
note :  the square root of two is shown as sqrt(2).
           the symbol for pi is not available, so the word pi is used.
 
 
angle in degrees angle in radians sine cosine tangent cosecant secant cotangent
0 0 0 1 0 undefined 1 undefined
30 pi/6 1/2 sqrt(3)/2 sqrt(3)/3 2 2sqrt(3)/3 sqrt(3)
45 pi/4 sqrt(2)/2 sqrt(2)/2 1 sqrt(2) sqrt(2) 1
60 pi/3 sqrt(3)/2 1/2 sqrt(3) 2sqrt(3)/3 2 sqrt(3)/3
90 pi/2 1 0 undefined 1 undefined 0

 


3.
Prove the following.

2cosx / cscx(1-sin2x) = 2 tanx

RS
2tanx

LS
2cosx / cscx(1-sin2x)

2cosxsinx / (1-sin2x)

2cosxsinx / cos2x

2sinx / cosx

2tanx

therefore, LS = RS
therefore,  2cosx / cscx(1-sin2x) = 2tanx

 back to home page