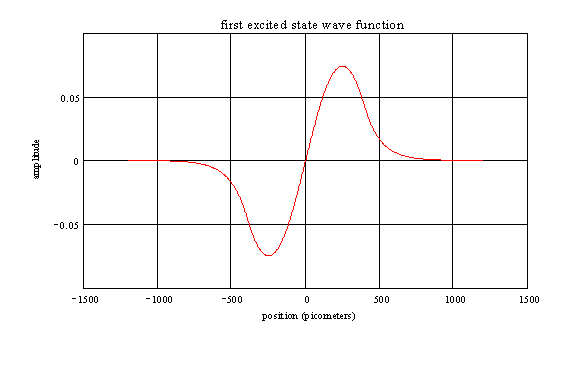
The graph below represents the first excited state wave function of an electron in a finite square well potential. The potential is zero for -L / 2 < x < +L / 2.

The answers to the questions below are all symbolic. They depend on a, b, A, B, L, and constants such as pi and 2. (upper/lower case is important)

a) The wave function inside the well is A sin(ax/L), and the wave function outside is B exp(-bx/L) for x > L/2, and -B exp(bx/L) for x < -L/2 where a, b, A, and B are constants.

What is the ratio B/A in terms of a, b, and/or L?

B/A =

b) Suppose that the position of the electron is measured. For positive x what is the most likely outcome of the measurement?

x =     

It is possible to solve for A and B, but the math is very messy. In the following parts, suppose that you know A and B.

c) What is the probability that the electron is in the well (ie. that -L/2 < x < L/2 )?

Probability(in the well) =

d) What is the probability that the electron is outside the well (ie. that x < -L/2 or x > L/2 )?

Probability(outside) =