Determine if the functions, y(x,t), below are solutions to the wave equation

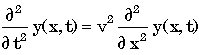
for appropriate values of the constant, v, the speed of propagation of the wave. Let x be in meters, t in seconds and v in meters per second. If the function is a solution to the wave equation, find the speed of propagation of the wave. If the function is not a solution to the wave equation, enter 0.

Remember that if you're not sure, you can always verify your answer by comparing the second time derivative with the second space derivative.

a) y(x,t) = 3sin(0.6x - 3t) + 2cos(0.2x - t)

v = m/s

b) y(x,t) = 4sin(2x - 5t) + 2sin(2x + 5t)

v = m/s

c) y(x,t) = exp(-(ax)²) exp(2abxt) exp(-(bt)²), where a and b are constants.
You must give a symbolic answer, in terms of a and b.

v =

d) y(x,t) = (1 + cos(2x-6t)) / ((x-3t)² + 1)

v = m/s

e) y(x,t) = 6sin(16x² - 25t²)

v = m/s