Consider a wave traveling on a string. The displacement of the string in the y-direction, y(x,t), as a function of position along the string in the x-direction, x, and time, t, is given by:
y(x,t) = Asin(2px /l - 2pf t + f)
The wave is propagating in the positive x direction. The displacement as a function
of time is shown in the graphs below for two positions, x = 0 m and
x = 0.03 m.
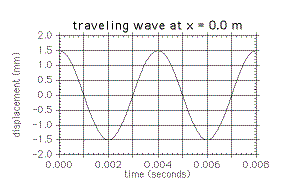

Find the values for the following quantities consistent with the functions shown in the graphs.
a) The amplitude: A = mm
b) The frequency: f = Hz
In order to calculate the wavelength, you must know the the speed as well as the frequency. The wave speed can be found from the two graphs: the peak that is at x = 0.0 m when t = 0 s is the same one that has moved to x = 0.03 m when t = 0.001 s. (You can check that logically these must be the same peak.) This tells us that the wave speed is 0.03 m / 0.001 s = 30 m/s. Now the wavelength can be calculated.
c) The wavelength: l = m
By choosing the phase, f, you can slide the graph to the left or right. Find the smallest positive value of f that correctly describes the above wave.
d) fmin = °