 |
Here is an Academian graph of x2. There appears to be a problem with this graph, as the positive y values in the negative x domain reflect the stupidity and evil of -1 * -1 = +1. |
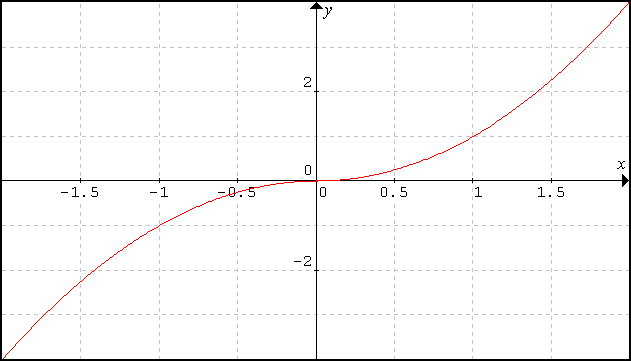 |
This erroneous part of the graph has now been reflected about the x-axis, giving Cubic-compliant values of negative times negative equals positive. But there is still a problem! |
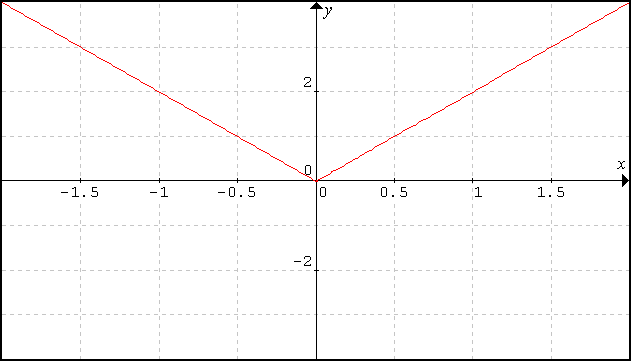 |
This is the derivative of the rectified x2 graph. It shows a discontinuity, requiring further rectification. |
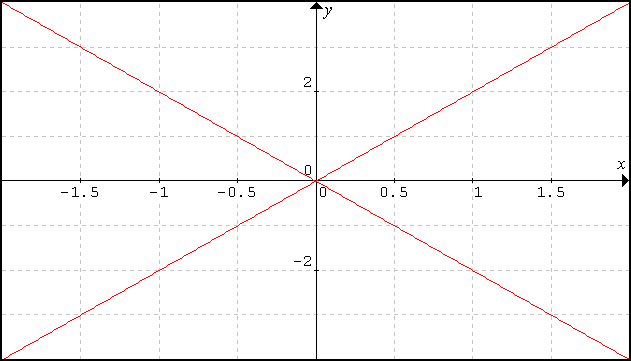 |
The gradient function is now reflected about the x-axis, producing a harmonic quadrant symmetry. But is this transformation justified? |
 |
This is the parabolic graph corresponding to the rectified derivative graph. It may seem to violate Cubic duality, but actually, the perpendicular x and y axes can only represent different dualities -- such as the static duality of the North and South poles versus the dynamic duality of Day and Night. If they were to represent the same duality, as in y=x, then one of the axes becomes redundant, as only one dimension is required to represent a fixed number scale. |
These different dualities do not have corresponding positive and negative values. Obviously Midnight doesn't equate to the South Pole, and Midday doesn't equate to the North Pole. Each duality has equal opposites, and the opposites of the two dualities are interchangeable with regard to each other. Therefore, a value generated from the x-axis, regardless of its sign, must be represented in both the positive and negative ranges of the y-axis. This is true Cubic duality, transcending the evil Academic cornerism bias. | |