Mathematical symmetry is
commonly found in
tessellations.
A
pattern is symmetric if there is at least one symmetry
(translation,
rotation,
glide reflection,
reflection)
that leaves the pattern unchanged.
Translational Symmetry
Rotational Symmetry
Glide Reflection Symmetry
Reflection Symmetry
Symmetries create patterns that help
us organize our world
conceptually.
Symmetric patterns occur in
nature, and are invented by
artists,
craftspeople, musicians, choreographers, and mathematicians.
Note: Tessellations extend to
infinity; the diagrams
shown below are finite portions of infinite tessellations.
Translational, rotational, and
glide refection symmetry are the three mathematical symmetries most
commonly found in tessellations.
1. Translational Symmetry - a tessellation has
translational symmetry if it can be translated by some vector
and remain unchanged. Any tessellation with this property has
inifinitely many different
translation vectors due to the infinite extent of tessellations. The
tessellation below
has translational symmetry; two possible vectors are shown.
2. Rotational Symmetry - a tessellation has rotational
symmetry if it can be rotated by some angle about
some point and remain unchanged. A tessellation which can be rotated by
1/n of a full
revolution and remain unchanged is said to posses n-fold rotational
symmetry. In the
example below, point A is a point of 3-fold rotational symmetry, while
point B is a
point of 2-fold rotational symmetry.
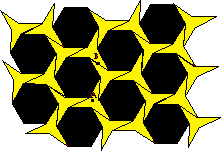
3. Glide Reflection Symmetry - a tessellation has glide
reflection symmetry if it can be translated by some
vector and then reflected about that vector and remain unchanged. A
special case of glide
rereflection symmetry is simple reflection or mirror symmetry, where
the vector has
a value of zero. The example below illustrates glide reflection. Try to
find some
lines of simple reflection symmetry for the first tessellation above.
How
many tessellation tilings can you find in your house? How many can you
find in
your classroom, in nature or outdoors? Locate examples
of real-world tessellations, scan or photograph them, and describe
tessellations
found in the real world (at three different tessellations per person
should be
included in your group presentation). Name and describe the examples
that you find. Turn in printed copies of the examples that you found.
What is symmetry? (Even though we
all understand and recognize symmetry intuitively, it
is a little harder to say just what it is.)
