other good places to visit...
C/L SPEED FORUM
FLYING LINES
electric calculator
I'm a poet...
...and I don't even know it...
shrieking, howling, singing
hanging motionless
as the world spins
the shape it draws
centers me
do I hold it to the ground?
or does it pull me into the air?
WELCOME! My name is John Strollo The purpose of this page is to reach out to modelers like myself who have a strong interest in C/L SPEED.
My 1st attempt at flying fast was with a self designed profile model with a 14 inch wing span, powered by a FOX 35 stunt. I convinced my wife to attempt a HAND LAUNCH [losing her as a potential pit-man forever] The airplane promptly wrapped itself down the lines. At that instant I knew I was doing Something Wrong.
Much of this material has come from direct conversation. Some of this material is paraphrased from articles written by a few of these men. Some of this information was written 30-40 years ago, but is still pertinent today.
Many of the people I talk to have VERY DIVERSE THOUGHTS ON THE SAME SUBJECTS.
I have tried a lot of these ideas, I AM NOT PROMOTING THEM AS GOSPEL. Try them out YOURSELF!!!

WILD BILL NETZEBAND wrote that most of the secrets of FLYING IN A CIRCLE were discovered a long time ago and some of them are stuffed in someones drawer or garage waiting to be rediscovered. Let's work on finding them.
I hope S/R saves you some time in your Quest to FLY FAST. If nothing else I hope it provides you with some "bench racing" material.
I am pretty far into electric flying. It is easy and not that expensive. I think That the KDE direct motor
Jets, specifically Sport Jet and B Electric are my interest now
the ubiquitous BABE BEE
a study in "art deco aviation", the JUGHAID

 My new interest in modeling is electric speed!
My new interest in modeling is electric speed!the "CATFISH" powered by a Scorpion helicopter motor...

I am astonished by the power that electric motors are capable of using LIPO batteries, which are much smaller and lighter than previous "chemistry".
POWER = WATTS
VOLTS = THE PRESSURE at which the electric energy is being delivered
AMPS = THE QUANTITY OR FLOW of electricity being delivered,
WATTS = V X A.
746 WATTS = 1 HORSEPOWER
...my variables [I bought the motor based on the price]
1. 1300mAh battery, 6 cells, lipo [the thing is gonna run for about 45 seconds and will use less than half of a well charged battery,
2. you need a timing device [to shut the motor off]
3. 100 amp controller[all you need for this set up]
4. SCORPION HK3026 1400KV MOTOR
A motor capable of speed flying
The motor must be able to handle the required power and the torque to turn a propeller appropriate for the model.
150 watts per pound = all out performance.
Remember that Watts = Volts X Amps. This is a power measurement.
746 watts equals 1 horsepower.
Competition 300 WATTS PER POUND
WATTS NEEDED TO GO FAST
Multiply the displacement of the recommended engine by 4000 [watts per cubic inch on an internal combustion engine] to find the amount of power required of the electric motor system.
For example; a decent racing .40 engine will make .40ci x 4000W/ci = 1600W of power.
Consider that the airplane will weigh about 2.8 TO 3 pounds with battery 2.8LBS TO 3LBS x 300= 843.75 TO 900 watts
NOT SO FAST!!!
REMEMBER THAT MOST OF YOUR DRAG [POWER ROBBING DRAG] COMES FROM THOSE WIRES [THE UMBILICAL CORD]
BETWEEN YOU AND YOUR PRIDE AND JOY!!!
5. THE PROP!!!...this seems to be the determining factor as to whether you go fast or you melt your motor, battery and controller!!!
A high-speed model will work best with a small prop at high RPM
6. COOLING...I always assume excellent cooling [expose the motor]
The battery is also a big part of the puzzle.
Consider the voltage required to see what kind of battery is needed.
The battery must be able to support the current requirement of the motor with the chosen prop.
DISCHARGE RATES (C) Discharge is the amount of power the battery can 'push' out and the number shown '20C' is an multiplication of the capacity.
For example; A 20C battery can discharge at 20 x 2,000mAh which is 40,000mAh or 40Amps. This is an important number if you know your motor requires a certain power level.
In addition to this, batteries have a 'Burst' rate, which is the amount of power the battery can discharge for a short period, usually 10-20 seconds.
A typical battery label may show 20-30C, this would mean a 1,000mAh battery can discharge 20,000mAh constantly or give a sudden and short 10-20 second 30,000mAh (30A) burst of power.
Tip: A higher 'C' rated battery will last longer if run at a lower 'C' rate. Example: a 30C battery run at 20C maximum will have a longer cycle life than a 20C run at 20C each flight.
C ratings are simply a way of talking about charge and discharge rates for batteries.
1C, = 1 time the rated mah capacity of the battery.
So if you charge your 650 mah pack at 1C, you charge it a 650 miliamps, or .650 amps.
1C on a 1100 pack would be 1.1 amps.
2 C on your 1100 pack would be 2.2 amps
So a 1100 mah pack (1.1 amp hour) might be rated for 10C discharge, so you can pull 11 amps ( flow ) without damaging the battery.
Then it might be rated at 2C charge rate (flow), so you charge it at 2.2 amps (2200 mah)
If you have a 500 mah pack - any kind - and it is rated at 16C that means it can deliver 8 amps.
If you have a 1000 mah pack - any kind - and it is rated at 8C that means it can deliver 8 amps.
If you have a 3000 mah pack - any kind - and it is rated at 10 C that means it can deliver 30 amps.

Some shots of my "BIG BIRD" RAT/40
designed to be launched by a stooge
Dubby Jett RIRE power



NIGHTINGALE HANDLE

Ashley Wilkes' 1/2a proto
note the sub-rudder
courtesy of Tom Wilkes

Two of Dave Cotton's Sport Jets
The will need some break-in, with Straight castor-oil fuel.. Start with some 'mild' fuel, (5~15% nitro) with @ 23~25% Castor oil... Medium-Hot plug. (K&B 1L or equal)
Run until you get a 'uniform' wear pattern on the top (sealing) edge of the piston, and the engine will run full lean, without sagging. Prop @ 1~1-1/2" smalller diamater prop, so RPM's about the same as in the air.
Start with a slightly "rich" setting, small prop, and @ .010~.015 head clearance, and then 'pinch' the fuel line to lean it out for a few seconds, gradually increasing the 'lean' time. Total runing time from @ 10~25 minutes.
IF IT 'SEIZES' and stops; Lap the piston slightly with some 800~1000 grit Aluminum Oxide Lapping compound, (straight-up position) and then sonic clean parts, oil re-assemble, and continue test running.
Then go to 25~40 % Nitro fuel, with the same procedure. Slightly colder plug.. K&B- HP, McCoy #8 or 9, Rossi/NOVA ROSSI #4 or 5... Repeat with 60~70% Nitro fuel.... One heat range colder plugs...
Changing from 15 % to 40 % ....SHOULD... yield @ 1K RPM increase, on the same prop. 40% to 70% SHOULD yield another 1K RPM increase. IF YOU DON'T SEE THIS MUCH INCREASE, OR NV SETTINGS ARE GETTING TOO CTITICAL, (Narrow) HEAD CLEARANCE IS TOO TIGHT, AND NEEDS TO BE INCREASED..NEVER MORE THAN @ .015" CLEARANCE THOUGH.. iF YOUR ENGINE NEEDS 'MORE' HEAD CLEARANCE THAN THIS, IT'S TIME TO CHANGE THE HEAD DIMENSIONS... (PLUG DEPTH, SQUISH BAND WIDTH, CHAMBER SHAPE/VOLUME, ETC.)
MORE RPM INCREASE THAN THIS, AND/OR TO 'BROAD' A NV SETTING, MEANS THE C.R. IS TOO LOW, AND YOU NEED TO DECREASE THE HEAD CLEARANCE...
HIGH (50~80% NITRO) FUELS NEED A HIGH AMOUNT OF 'SQUISH' TURBULENCE, AND LOW HEAD CLEARANCE,AND A DEEPER DEPTH, 'COLD' PLUG TO ACHIEVE MAXIMUM RPMS. ON BALL-BEARING ENGINES, THIS IS USUALLY @ .002~.010" clearance range... THE HEAD CLEARANCE WILL ALSO NEED TO BE ADJUSTED FREQUENTLY DURING THE DAY,TO KEEP UP WITH THE WEATHER CHANGES, WHEN RUNNING ON THIS 'RAGGED' EDGE OF THE PERFORMANCE ENVELOPE...
I ...DON'T... RECOMMEND RUNNING MORE THAN @ 40~50% NITRO IN YOUR PLAIN BRG. ENGINES.... AND THEY'LL LAST LONGER WITH 25~30% OIL in the fuel...
Your S.T. C-35 engines have 'Soft' Crankshafts.... Try the 'Double-Bubble' heads from the G-21/35 (BB) engine, IF you can find any...?
Cheers, Glen
My associate Robert Gray and my old flying buddy Sonny Williams and I have spent several months (retired as we are) doing considerable exploring trying to find some possible fresh useful information on P-J engines.
We appreciate very much the assistance we have received from present and past jet flyers to give us a good starting point in this project.
However, we wanted to see if there were some other sources of P-J info that may have not been explored fully, or at all, as having possible application for C/L Jet Speed Flying.
We had explored thoroughly all of the Jet articles on Tom Wilk’s “CD #2 U.S. Speed” which is a must for any serious speed flyer. $10 at www.cpinternet.com/~tawilk36 .
This CD covers Speed Times issues from 1982 to 2003. It’s a shame something has not been worked out to allow all of the later issues of Speed Times to be placed on CD. They are truly a valuable source of Speed information.
We have reviewed info on full size and model size Valved Pulse Jets, Ram Jets, Valveless Pulse Jets and anything else that might have cool air coming in the front and hot air going out the back.
The Internet makes available information that would have been impossible to assemble in the past.
We have had considerable communication via the forum at www.pulse-jets.com with “Pulse Jet Enthusiasts” that design and build their own engines.
We, as a group, have generally been modifiers of engines that we have had available.
First the DynaJet, then the extended Thomas head, some had equipment to custom make low port bore angle extended heads, Hoyt/Davis/Raven head and Bailey pipe as built by BMS and now the Jet Bill designed heads on the Bailey designed pipe. These are the engines that we have applied Dremel tools, files , sandpaper and polish to supposedly make them a little more powerful.
But have we fully explored how they really work in order to get the most out of these noisy little beast?.
We would like to share with you some of our findings that may be old “stuff” to most of you but there may be a “tid bit” or two that will spark your own thinking in a new direction or add something to what you already know.
We will start with the “jet master” himself, Franco Marcenaro whose pulse jet theory article first appeared in a 1983 issue of NASS’s Speed Times, Vol. 2, No. 4, starting on page 13.
This article is on the previously mentioned CD. It may also be downloaded from the Internet. “Advanced Pulse Jet Theory”http://users.bigpond.net.au/pulsejet-pjaa/theory.html This will get you started in what goes on in these engines and especially with the function of “waves” on the P-J cycle.
Here are some other sites on the Internet to take a look at:
http://www.aardvark.co.nz/pjet/howtheywork.shtml From www.aardvark.co.nz/pjet
Bruce Simpson, a very basic and informative text and visual description of P-J cycle.
Also, home built P-J info and videos of P-Js running with sound!.
www.beck-technologies.com
Eric Beck – he has a forum – and much info on “home built” designs and pictures. Very valuable.
www.pulsejet.,amtjets.com
Netherlands engine design
www.precision-technologies.com Troy Legner’s P-J engine
www.pulse-jets.com
Forums on Valve and Valveless Pulse Jets. Valuable info on both. Also on the home page, there is a listing across the top of the page, a little hard to read, click on “Forum” and also click on “Pulsejet”. On the latter you will find a lengthy paper by Fredrik Westburg “Inside The Pulse Jet Engine” and also a list of P-J engine drawings for download.
Check out the “Soviet FAA Class” drawings which are the Ivannikov World Record engine. Note these postings relative to C/L P-Js: “Pulse Jet Intake Air Velocity,” “C/L Speed Fuel Systems,” C/L Speed Engine Design,” and some comments about Franko’s paper: Franko Marcenaro Comments.”.
Another source of valuable info is the Russian P-J Engine Book (1958 103 pages) available from Rocket Science Books via e-bay. The price seems to bounce around. Best I have seen is $10. The illustrations are worth the price of the book even if none of us are able to read Russian.
These guys had it “together” on P-J info as far back as the late 1950s and a small amount of this info made it into issues of the British Aeromodeller magazine thru the years. That is where the text and drawings of Lipinsky’s 245mph record ship appeared in the 1972-73 ANNUAL.
There are also some valuable points to be picked up on several NASS Forum posts: Sport jet Rules, Thrust, Line Rake Calculations, Go Fast on Alkie, and the 4 part series on Jet Speed History . www.clspeed.com Then in this order: Speed Forum – C/L Speed Forum – General Discussion – then click #### msg. to get the full list to come up.
COMBUSTION CHAMBER (CC) What is going on in our P-Js? .Let’s start in the middle of the combustion cycle. We have just had an explosion and exhaust gases are going out the pipe and the reed valves are starting to close. We now have negative pressure (vacuum) forming in the CC and this results in some of the exhaust gases being “re-ingested” back up the pipe.
This is where the flare helps out when the ship is at rest or the engine is on test stand (static).
Some say the flare is not needed at high speed, but I have not heard a first hand report of anyone trying this. Dale Kirn drilled perimeter holes around the flare but got no performance change. It will obviously kill much static thrust and the ship may be slow getting off the ground or give you an obviously low reading on a test stand.
It was reported that Earl Bailey had a pipe flaring tool at one or more test sessions and “tweaked” this flare for optimum results. Does anyone know if Bailey ever tried a longer CC and then backed down to the length that went in to production? You would have to keep the pipe the same length to properly give this evaluation.
Back to the “ingestion” of exhaust gas. This returning charge has at least two effects. First, it reignites the air/fuel in the CC for the next cycle. This continuing ignition is not caused by the heat from the CC.
Next, this returning charge acts as a compressor for fuel/air that is now coming in around the valves into the CC. This would be slightly like, but not identical to, the compression that takes place from the returning charge of fuel/air on a tuned pipe two stroke. We may or may not have some wave effect on the P-J to assist in this compression.
It is believe that the portion of the returning charge that makes it back to the CC does not contain much if any usable oxygen, but is just spent exhaust gases.
Some illustrations refer to the exit of the exhaust pipe as the “nozzle.” It appears more likely that the tapered portion of the pipe is acting as the “nozzle” as you would have in other jet engines or rockets with out an “exhaust extension.” The extension portion is, of course, a part of the overall length that the wave lengths are calculated on from the tip of the pipe to the back of the head.
It is of interest the different types of nozzles (taper) of pipes on small size P-Js. Most appear to be dictated by fabrication methods or equipment.
Why the DynaJet designers arrived at the extreme curve at the taper when previous P-Js (Buzz Bomb etc.) had very low angle tapers is still unknown. The taper on “home builts” varies considerable. The Bailey F-J pipe makes sense with a way to stay within the 1.25 sq. in. area rule using the megaphone and larger exhaust pipe.
However, it brings into question as to why the Sport Jet engine used the small pipe rather than the same large one, or at least a non tapered pipe with 1.25 sq. in.. area which would have been simpler to fabricate..
Now this may be a new thought for some of you. Before the valves have time to close (they are not moving nearly as fast as the returning exhaust gases) there is spent combustion gas that goes forward around these valve petals and into the intake.
There is an illustration of this in the Russian Jet book and there are others on the P-J Forum who are in agreement with this.
So it appears that at the start of the intake cycle, the first gas to enter the CC is at least partially spent exhaust gas ... not a fresh slug of fuel and air from the intake.
INTAKE: There was an old expression back in the Hot Rod days: “It’s What’s Up Front That Counts.” That has generally been the case with our P-Js.
LENGTH; We have found nothing to tell us why the 3 - 3-1/4" intake performs better. The Russians used a cowl/tank/intake about 5" long for their engines. Maybe this is what it took to get their fuel capacity while staying within a minimum drag pipe diameter.
There was a 5" long head and a Thomas head that went for less than $200 on e-bay several months back. I wonder if the original owner from Ohio had ever tried it?
The “home built” or “Pulse Jet Enthusiast” and Europeans don’t seem to “think out of the box” on head design and have continued to stay with basically copies of the DynaJet configuration.
PORT BORE ANGLE: Jerry Thomas stuck with the old DynaJet 24 deg. Port angle. The BMS Raven was 15 degrees and Jet Bill has settled on 16 degrees. Same thought as above from “outsiders” applies here.
Most of the “P-J Enthusiast” drill the ports DynaJet style or use a separate back plate. In either case, they make their own reed valves to cover some very big port openings.
VENTURI or INTAKE BORE. Most ‘home built” engines are using venturi shaped intakes even if they have another way of getting fuel to the engine. A lot are using liquid propane as an easy way to get their engines to operate for their static stand experiments. Others use petroleum and methanol fuels.
When pressure fuel systems were perfected in C/L Jets, it enabled the intake throats to be enlarged. They seem to have settled at 1 1/4" I.D. The only reasoning we see here is the old Hot Rod reasoning ....... “Bigger Is Better.” Our discussion will give some further insight in this area.
COWL/INTAKE CONTOURS: Pull up this Internet site and review the text and illustrations. Http://en.wikipedia.org/wiki/jet_engine At that site, go to “Air Intakes” and scroll down to item 6.1.1 “Subsonic Inlets.” We think this and additional information throw some light on why the “bull nose” or “blunt nose” cowl works.
It was evidently an accidental beneficial discovery that no one has fully understood. This type cowl is a “one size fits all” solution to an intake situation that there is no perfect solution to short of a variable intake system. We have air flowing thru the intake at speeds from zero, at time of close valves, to possibly approaching 200 mph at top speed.
The more powerful leaf blowers have an outlet velocity of 200 - 230 mph. How would choking off your P-J engine with fingers over the intake compare with the leaf blower? If you have some info on intake air velocity, please let us know. Check out the “P-J Intake Velocity” post on www.pulse-jets.com for a discussion of this. At rest (static) there is no problem with the entering air with some of it even coming from back and around the cowl.
However, as the aircraft begins to move and the valves close, the air is forced to spill out and around the cowl until the valves open again. Obviously the faster you go the greater the amount of spillage becomes and the leading edge curve becomes even more important.
The “bull nose” evidently helps the aerodynamic flow of this spillage by causing significantly less drag. Notice the description of the “Streamtube” which is only going to act perfectly at one instance in the pulse cycle. The rest of the time we have various assorted conditions but it appears that in almost all conditions the outside airspeed is going to be faster than the average air speed going into and through the intake.
There is another problem we have with the intake. This is referred to as the “Vena Contracta”effect. (A description will follow) . Dick Hall and I had discussed this phenomena in 1972 when he had observed fuel/air flowing back out of a straight bore recip. two stroke engine intake.
We had discovered the same thing with a 196 mph record setting jet that had evidence of fuel/air flowing forward in the intake and out and around the cowl.
Later discussions with Dick and Don Monson in 1974 led us to the reduction of the intake diameter on the nitro burning 212 mph record setting Super Burp. The other thing that can take place with an intake having improper curves is the stall factor on the intake entry.
I watched a movie at one of our model club meetings in the early 1970s that showed a wind tunnel test showing at certain stall conditions on an airfoil the boundary layer of air actually moved forward toward the leading edge. As I said before, a cross section through our jet intakes is an airfoil.
Both interior and exterior work together like top and bottom of a wing airfoil. On the “bull nose” cowl, the air speed differential between top and bottom of this airfoil is amplified even more by the high curve of the top and the difference in air speed going in the intake and that going around the outside of the cowl. Add to that the fraction of time that you have a “wall of still air” at the intake entry and all of the “streamtube” having to divert out and around the cowl and you have a very strange unknown phenomena.
DIFFUSER: The rear chamber of our intakes is a true diffuser. The total surface area of the port bores prior to the valve surface is greater than the total area of the intake bore. This causes a diffuser action with the air velocity being reduced and the pressure increasing in this rear portion of the head. It is desirable to slow down the fuel/air charge so that the “flame front” does not just blow thru the CC.
VENA CONTRACTA: I just received a reply from a recent enquiry I had made to Dick Hall, a retired Missile Engineer at Redstone Arsenal. I quote: “You mentioned me telling you about fuel flowing back out the top of a straight bore venturi. (1972 discussion, bp
I talked to a modeler friend who was the head of the aerodynamics section at the Arsenal. There is a technical term for what was happening called “Vena Contracta.” Latin for something like “entrance contracted.”
The best way to visualize what was happening is a bucket of water with a hole in the bottom. If the hole is just a plain round hole in sheet metal, the stream leaking out will be smaller than the hole diameter. If the hole is flared with sufficient radius on the inside, the stream of water can be as large as the bore of the hole.
Without the flare, the water flowing in from the periphery of the hole pushes toward the center and restricts the flow. When air is involved instead of water and without an entrance radius, the air flowing in around the sharp entrance pushes toward the center and causes turbulence along the inside wall which can actually flow in the opposite direction along the wall.” This link will help show the effect through an orifice but does not cover possible turbulence along the wall of the flow path. http://en.wikipedia.org/wiki/vena_contracta.com
We hope that this information will be food for thought and give us all a better understanding of the operation of our beloved pulse jet engines.
It has been an enlightenment, to say the least, for Sonny, Robert and me. Mike Langlois has probably been buried by all the e-mail copies as we have tried to keep him informed..
Do not hesitate to copy, forward, publish or do what ever you want to do with this information to give it the widest possible distribution. We think it is of value for most jet flyers and others interested in the operation of the pulse jet engine.
Bill Pardue
April 15, 2007
www.pardueatticus@aol.com
This is from Bill Pardue, the famous jet speedster who along with Mike Langlois, set what I believe is still the fastest official AMA JET SPEED flight in a contest...
With so much jet info flying around lately on the Forum, I thought I might try and round up some info on the history of jet flying.
Around 1996 Don Laird did an amazing job of putting together a "kit" of info going back to the invention of the pulse jet, and going thru significant jet articles, plans and engine drawings. Tom Wilk's CD has much jet info and later articles in Speed Times from early 80s thru 2003. The recent info on the Tarfu design sort of brings things up to date. Mike Hazel put together a "jet pac" about that time with other pertenant jet info.
To run back over all of this would take forever, so I thought I might aim at modifications to the Dyna Jet engine and later original engine developments. The most important thrust of this, is of course, the head.
The original patents showed heads with round ports and "pear" or "petal" shaped ports. Dished out retainers, pressure fuel off the combustion chamber and other features that others later "reinvented." It seems that the Tenney petal valve system was a reinvention of a 1925 valve system for air compressors.
A close look at the plans for the alleged 179 mph record ship show the tank being on the inside of the circle with the pick up line about 2/3rds back from front and inline with c/l of engine.
A recent phone conversation with Tommy Baker reveals that he had dished out and cut back retainer, backup valves, and wing dihedral to put line outlet point at the wing tip at the center of force which was more recently reinvented by Glenn Lee with his modifications to the basic Hoyt Sidwinder design which in turn led to the present Tarfu type 3 level ships. To top it off in the early 1950s, Baker had discovered that low octane white gas was better than his Blue Sunoco that he had previously preferred.
Herb Davis "Hot Canary" of 1950 was the ship that we all copied up until the Hoyt Sidewinder.
Back to the head. I had previously thought that Thomas & Fisher were the first to mess with the extended head in the late 1950s when they were trying European style fuel tanks enclosed in the cowl. They noticed an increase in speed which led to the Thomas extended head modifications to the Dyna jet.
The cowl configuration allowing for the radius intake leading edge was just as important as the extended head, in my opinion. Doc Davis gives Jim Summersett credit for the "bull nose" cowl on the stock Dyna head that was originally molded from the typical Hotel pot bellied water glass. This bull nose seems to be preferred by most today. I personally favored the Thomas type leading edge with Mike Langlois and I used on our Thomas type heads in the late 70s.
Back to the origin of the present nominal 3" long extended head. I have finally found all my old jet files with info going back to my 1953 Lil Burp design.
Dave and Dale: You wont believe the notes I have from info you gave me at the 1958 King Orange meet and later letter from Dale trying to help me with fuel and retainers. I have my sketch of the ports "pear shaped" in Cotton's head and ....... quote "One head had extension. The other not. He tried non extended head. Flush washer on retainer. Head extension 1 7/16" long from smallest diameter of venturi." My sketch of the head shows stair stepped joint at the small point of intake and notes "Spraybar spaced out same distance as head is extended. Tank pick up stops under holes in spray bar." "Retainer similar to Kirn's . One cut to shape of veins." sketch shows retainer the shape of reed valves. My sketch shows the cowl being typical with sharp leading edge with note pointing to rear section of cowl "cowl splice here." So front must have been Squirt or spinner type cowl.
Notes on "Kirn's retainers." "Hollow out back 1/16" to 3/32" thick. Cut back from front .060 or .080 as measured from back for more vein opening." I wont go into all the fuel info, but this: "170 mph benzol 50% - white gas (cheap) 40%. .060 retainer. 3rd attempt on .080 retainer."
In a letter from Dale dated April 7, 1959, Dale had tried the new .028" line. 1st flight 153 on .024. 2nd flight 144.26 on .028. 3rd flight 152.87 on .024. All flights on 100% "Quik-Sol" and stock retainer. He then noted that his 170 mph KOI flight was on 60% white gas and 40% Quicksol. My notes go with much more detail Kirn's and Cotton's fuel formulas and tracking down what "Quixol" actually was.
Also Ted Black's fuel formula that we used for years. I could write reams on fuels as that was my "cup of tea" up to and including the popular 50-50 nitro propylene oxide formula.
It's your turn, Dave. Where did your extended head design come from? Did it ever work? Your set up did not have the radiused leading edge that I always thought was all importance after observing Jerry's head for the 1st time. Did your work "dead end" as it appeared to and Thomas coincidentally come along at the same time? Did you and I even get clockings at that KOI behind Dale's 170?
I still remember my early thinking on the Thomas head was that it was helping straighten out the air coming in the intake of a yawing upright engine. Remember, the Sidewinder guys were saying that the extended head was not giving a performance increase.
The Ohlsons were the first to get them going on the Sidewinder, as far as I know, but I don't think they had the right cowl .... if any. And I think they were the first to successfully run pressure on the Sidewinder.
(anyone know where Mike Hanbeck is for Hoyt Raven early development?)
Before and after Mike Langlois 212 mph record there were great rumors of fast flying from Hoyt's 214 in Canada to other fast test flights ..... they don't count. Doc Davis broke Mike's 1st 211 record with another 211 .... then Mike's 212 which stood until the fuel change. (I think that is correct).
On Don Monson's recommendation we had dropped the intake down to 1 1/4". No thrust on ground, but set records in air and won the 76 Nats. My understand from Doc, I've still got his letters, was that they went to the reduced intake for his fast flights. I guess that was with his version of the Raven head ... rather than Thomas type.
Mike Fiske: Can you help me get from the Hoyt Raven, which was originally a modification to the OS head, if I am correct, and then later an original head, .... to the Texas Davis/Perkins/Bailey head.
I take it that Doc's fast flights on nitro were Raven with 1 1/4" intake. Now you guys went to work to get rid of the terrible MEK fuel formula and turned up with the workable 80-20. I take it at this point the intake opening went back up to 1 1/2" to get more air to the alkie.
Mike Hazel: What was Jerry doing at this time? Evidentially he and the Kirn's teamed up with some fast flights. Was all this on nitro ..... or did Jerry get some fast flights with his asymmetrical on alkie. Pictures appear that he stuck with his original head design thru all of these changes.
Someplace along the line the Bailey "Raven" was modified or either an original head by Mike Couts that in turn evolved into the present Jet Bill head. Patrick Hempel and Joey are still running their versions of the Raven head. Couts seemed to have preferred the Thomas type cowl vs the bull nose. I understand that he sold everything, moved and went in to flying full size sailplanes, so can't pick his brain.
O.K., guys .... help me out and fill in some gaps. Also any significant points that you remember in airframe or engine design along the line. I would love to see a list of the Jet Records and Nats wins thru the years. I can't even find my certificates for records we held and still can't figure out where we placed at the Nats thru the years.
I did find out that Harold and Ricky Berrier were at the 60 Nats flying jets, but I didn't go to Dallas with Harold until 63 or 64. Harold died a few years back, so I can't call on him for reminders of the old days, along with Black, Thomas, Hempel, Perkins, Bailey, Waltermath. Doc Davis and probably several others that I am not aware of their deaths.
I would like to make contact with Mike Hanbeck, Bud Elder, Jim Summersett, Dick Hall, Jim Davidson and Seabert Parsons if anyone has info. I was last in touch with Dick in 1969 and Summersett around 1979. Baker is still in Kings Mountain, NC and the BGH crowd are still in the High Point, NC area and Langlois in Greensboro.
Let me hear from you .... thanks, Bill Pardue
So there you have it, Jet speed from an historical perspective by a guy who lived it.

More Cotton Magic
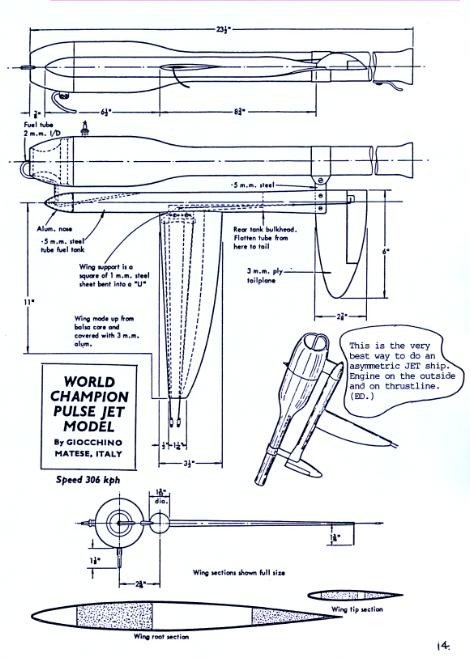
how about this ancient jet speedster from the old country [ITALY]

The Italian Stallion, in the flesh! [see the flag of ITALY on the stab?]
Here's a little tidbit from our NASS President, Bill Hughes, on the service of K&B bearings. Very informative
The crankshaft is pressed into the bearings on those engines. Like the 4.9. The split collect can be removed by screwing a 1/4x28 bolt in to the shaft. Using a gear puller on the bolt and the arms in the slot in the prop drive. It will make a pop and the aluminum prop driver will come off. You will then need to press out the crankshaft. You can use a Drill Press as the press.
Close the drill chuck all the way, press on the bolt head that is screwed in to the front of the shaft. it shold press out.
Reassembly is much more work. You will need some tools/fixtures to do it right.
1st. press the rear bearing on the shaft..all the way. pressing on the inner race only. spl tool required. Then warm the front case to about 200 degs. slide in the shaft/rear bearing. Then, while still warm, press on the front bearing, pushing on the inner race only...special tool needed. While doing this you will need to make sure that the crank/rear bearing has not moved back out of the front. case.
While still warm add the collect/prop driver and an old prop. tight it down like you mean it! The set up should spin nicely.
If not, tap on the stud/bolt with a wooden hammer to seat things a
little better. (I usually don't like to do that, the bearings can be damaged sometimes).
To get the cylinder out, warm the case up to maybe 200 degs. not too hot, these cases warp easlily.
Use a piece of wood. stick it into the exhaust and turn the engine over with a prop on it. The piston/stick will push the cylinder right out.
Don't drop the cylinder. They are pretty thin and a drop
will warp it.
Bill Hughes
Soooo, if you are inclined to work on your K&B, or any other BB engine, there are some guidelines from a Master Modeler
A pair of F2A trainers by Bill
I have moved twice in less than a year, from upstate New York, to Maine, then to North Carolina. I have all of my modeling stuff, but have not flown a thing. I love speed flying and will return to it asap. Meanwhile, be sure to check in at the forum, and join NASS!!!
I'm sitting in Maine right now, but I now work in North Carolina. It all took less than a year. When I get a chance, I'm gonna try to look up Mike Langlois.
Ned Morris, my old telephone mentor, is gone. He was a gruff man, but he had a good heart. I hope that he is flying.
Well, I'm outta work. This is bad and good. The bad is "...no paycheck...". The good is "...more time to model...". Of course, I'll need money to live and model, but I'll figure that out.
two years ago...
I went to Cinti. I left Friday at 6am, got to Jet Bill’s at 1pm or so and met JB [who is now the proprieter of a 1st class auto repair shop]and Richard Hart, from the UK, who bought BLUE THUNDER [I’m crying as I write this, we are losing THE THUNDER]].
Dick is a good fella who has lived in several of the world’s garden spots, including Iraq and currently resides in Houston, TX.
I followed JB and Dick down to Cinti where we stayed at a RED ROOFINN. I had hoped to do some practice flying that evening, but we got down late and heck, who needs practice?
Anyway, next day we went to the site and said hello to all, then I got out Bertha, my .60 trainer and went to the practice circle to have my own "meet". It would be the first time I flew since August and believe me, I NEED TO PRACTICE!!! I stayed there and got a few flights in with Bertha, was feeling good, took out the GRRT and got stymied after the first flight. Air leak, couldn’t get a setting. I decided that I had wasted too much time, so I took out the contest 40. Chris Montagino launched it for me, but the lines hooked a blade of grass on the infield, which flipped the airplane, broke off the gear and ruined the Kelly prop and my good set of lines. [I have more sets of practice length .020’s than anyone else in speed].
I almost packed up and went home. Of course, throughout my little self-absorbed day, there was a good contest going on.
Spent most of Sunday morning fixing stuff on the 40, went and took a flight and got my usual 145ish time, took another flight and got a little up and down so I pulled out of the pylon [didn't think the gear would take another pancake] and that ended my contest. Nothing like driving 600 miles to take 2 attempts!!!
I was oblivious to the carnage going on around me, all sorts of mishaps, guys hooking the controls backwards, bad fuel for the jets, crashes and assorted mayhem. I thought I was the only one that did these things!. JB lit a jet on fire, it was the eventual contest winner, Mike Couts’ asymmetrical JB did all the pitting for every fast contestant. I feel that if he just did his own thing with Mike, he could have won. But he loves it and I think he likes to help. It sort of sets up a challenge for him to shoot for.
The A/F2a guys were going at it. Tommy Brown, Chris Montagino, Bill Hughes and the Great Carl Dodge were nipping at each other for two days. Fella's, there is some great RTF F2a equipment out there, all of it is well worth the $$$, but after watching these fella's for two days, this is not a good place to start flying speed. These guys are great, not good, GREAT, modelers and they had all they could do to keep those airplanes sorted out.
I couldn’t believe the cast of characters! GLEN LEE, DODGE, AL STEGENS, DAVE COTTON, FRANK GARZON. Ned Morris made an appearance, but just to say hi. The total experience level was incredible! There was me, right in the middle, asking for tools, parts and advice, getting it all.
Dave Mark and Barry Tippet [2nd and 1st respectively in 40] were once again gracious enough to help me get going. I think Dave sees me as his project, as well I am. He is without a doubt the most influencial guy in the sport for me, JB being a close second.
JB has tried to help with Jet, but I’m behind with that program. I feel as though I can at least fly 40 for sport/practice at the local parking lot. Nothing to do with jet except light it off once in a while to piss off the neighbors [and my wife] Jet will have to wait, but it’s always foremost in my thoughts. I basically go to the contests to play with the jets at night.
Well, sometimes speed is a calculated effort, sometimes it’s simply a war of attrition.
Chuck Whitley shows up to watch, his B speed is sick. He decides to pull his 1/2a proto out of the trunk and let Tom Brown fly it AND HE WINS 1/2A PROTO! Think if he would have not come. I make one official, hang it up, Glen Lee doesn’t enter, Chris Montagino spins in and has no more attempts, Bob Ytuarte has a torque roll....and I hang on to take third in 40! All I did was show up and fly my usual 145!
Chuck and I were pleasantly surprised for our efforts, all we did was try. I was glad that I didn’t head for home the night before. I was also glad that I had some good guys around me that kept encouraging me.
I also witnessed some of the better competitors have several mishaps that I thought only happened to me! As much as we would like this to be a science, you know, put part A to part b and go fast, it is still about testing your WILL. Who will be tough?
Do you know how I define toughness? It is the ability to perform, no matter how you feel. Believe me, toughness is a big part of speed flying. Talent is much less so...
I spoke with JET BILL about Blue Thunder and was surprised to find that the dogleg setup [outboard swept wing] is NOT figured for how lift from it effects C/G. The center of lift of that outboard wing is behind the C/G.
To me, this must act more like a stab in that all the "lift" generated at any angle of attack is behind the C/G. The thing has to fly stable.
We know that flaps on stunt ships are used to increase and decrease lift generated by the wing. We know that the elevator on all C/L airplanes is used to adjust pitch. Flaps without an elevator work like an elevator. If flaps are used alone, down flaps will produce a downward pitch if the c/g is far enough forward of the wing’s chord.
The airplane always rotates around it’s C/G, so increase of lift aft of the c/g will pitch nose down. However, when down flaps are used in conjunction with up elevator, the nose will pitch up, since most airplanes are designed to have the stab and elevator overpower the wing and flaps. Tail volume, that is, the length of the tail moment plus the stab area is usually more powerful than the short moment found in the c/g to flap hinge line.
I like to think of a c/l airplane as flying in a hemisphere. When the airplane changes pitch, it can only climb to the highest point in the hemisphere. After it passes that point, it’s now diving…up elevator quickly requires down elevator, if the high point is passed you should give it more up[ better to give up at the high point than down at the low point, that's how I modified my jet pipe] or the airplane will attempt to enter the hemisphere under the tarmac.
What if you were to balance the effects of the flaps and elevator so that up elevator would only control the downward pitch produced by down flaps? Wouldn’t this allow an airplane to change altitude without changing pitch?
I feel that this would be better than all the precession problems associated with changing pitch. The airframe would have to be stable enough to overcome pitch disturbances, but I think that a large stab would take care of this.
I've forgotten how to fly. Strange statement, I did fly an official flight in F-40 at this years NATS. Oh. I can fly, I've just forgotten how.
Let me explain. When I first started getting into C/L, I built and flew lots of trainers. I would fill them and fly them. I'd get 6 to 10 flights in a hour, hour and a half. I grew comfortable, started to shorten the lines, used hotter engines and 2 years ago flew 3 officials in 40 at the nats. I felt very confident and stopped flying trainers.
Well, since then I've gotten a new job, moved and had a fairly serious health problem...and I've forgotten most of what I know about control-line flying.
I brought my big monoline trainer to the nats and was flying it at night. Joey Mathison asked to fly it, did and deemed it a "hoot". He told me it pulled like a 40 and turned about like a D going 180. Hmmm...
As I drove back from Muncie, I decided that I would return to "fill and fly" practice. I could use a stooge and go like I used to, 2-3 times a week. I did not have to depend on anyone except the weather.
Tonight's session was with my old clipped wing Ringmaster, FOX 40 and 52' lines. As you may know, I'm a football coach and coaches teach HABITS!
I cut out a plywood disc [bathroom sink] and used it on the ground to make me "WALK" the circle rather than just rotate. I forgot how to use a regular stunt handle, so the first flight was a rotation special. I strung up my competition handle to settle the controls down and began my "workout". I figure to have done 6 flights at 35 laps per and have a whole new appreciation for racing events. I forgot how to land and was pancake landing all night till the last flight when I greased it. By the end of the session I was flying laps without looking at the airplane, I was looking down at the plywood "spot", simulating [to me] trying to get into the pylon
Practice flying with fill and fly airplanes has been good to me. I hope that I can learn how to fly again!
Made it to the nats!, I was working on my bathroom remodeling project....moaning...and the Missus gave me a "GET OUT OF JAIL CARD", so off I went.
Tuesday, I had Doug Gray's .21 and tried to set the needle...too lean [twice]. Barry Tippet informed me that there was some protest about me flying Doug's entry, so that was it for Tuesday.
We tried to fly my sport jet Tuesday night, but only succeeded in lighting it on fire. Jet Bill later told me that priming a sport jet is not necessary and fire can result. Chris Montagino won F2A for the second year in a row. John Newton showed me his kit .21. Great looking and flying! get one if you want a .21. So much for Tuesday.
Wednesday was a watching day, A and B are much past my capabilities. Newton and Joey Mathison, who comprise the NEWMATH team, won A speed. Joey is a real cut-up and a great pilot. Got to meet Marty Shoenheiter. He is a real craftsman. His new 40, the "SR72' is a black beauty that flies like it's on rails. That night I tried to fly my 40, but I'm now gun shy about the pylon.
Thursday was my last day and I was scared to fly. I asked Chris Montagino to fly for me and with Dave Mark's help got two officials, but I was embarrassed that I didn't fly myself. I decided to go for it on my third attempt. Chris and Dave pitted. I got a good setting, got into the pylon and got right back out after 6-7 laps. I landed, got some fuel and Chris wanted to take it, but I said I'd do it and I did. They got me going again, I got in and flew a complete race. I felt relieved. I want to thank Dave and Chris for coaching me through...it would have been a long winter if I hadn't flown myself.
That night, I hung around and we played JETS!!! Jet Bill was there with BLUE THUNDER and was making it look easy. Mike Fiske and the Hemples were there, Dave Cotton too. Lenny was there but wouldn't practice...he remembered last year and didn't want to chance it. Joey was flying, he is a GREAT pilot!
I volunteered to pump for the Texans, Mike Fiske is a real "PRO", he has a great program.
In return for my pumping, the Texans got me up with the SPORT JET. It was getting dark and I was in heaven watching that gizmo roaring around the circle, flames shooting out the tail and the tube glowing!
I was just out in my driveway with my buddy JIM. I showed him how easy it is to fire up a sport jet. He was impressed...but my wife threatened to call the cops!
My compliments to NASS, and especially Barry Tippet. This was a well run contest. Barry also took places in 40 and .21 proto as well as flying for several guys.
This was perhaps my best nats...I got to overcome a weakness, learned a little about setting a needle and those night jet flights!
The guys were the greatest too! I'm so glad to be part of this.
Maybe I can still get some jet time in!
I decided to live a little, so I packed up my car and headed to the Cinti contest held on Father's day. Cinti is how the locals abbreviate Cincinnati, not the more familiar "Cincy", as I am used to. Whatever you call it, it's a great town. I had visited several times before, but all for football related business. This would be the first time I would go for airplanes.
It's a great town, especially when your host is Tom Brown and his lovely wife Darlene. These two folks are international F2a competitors, Tommy is of course one of the famous Brown family members. Darlene is a lady who can pit, I saw her staging a pipe for Tom. She is very skilful. Tom and Darlene hosted a cookout for the contest attendee's on Saturday. These two folks love airplanes. They obviously love each other and were willing to extend themselves to those of us who came to the contest. We had a great time!
Tom, who happens to be one of the WC team members in F2a, put on quite a show in A speed and F2a, the airplanes he flys are jewel like and they look like slot cars when they "hit the pipe"
I asked Tom for some advice and he told me to "practice"...there is quite a bit of wisdom in that statement.
Since I am not an expert at speed, I would like to relate my experience in a less technical manner. Basically, after the Nats two years ago, I went home and hung my 40 on the wall. I changed jobs, we moved etc., so when I arrived at Cinti, I hadn't flown, except for a handful of sport plane flights in TWO years. When I saw Dave Mark, who is one of my mentors and a great modeler and competitor [he won 40], he asked me if I was ready to "go" [fly]. I said no, but he assured me that flying was like riding a bike. If it was like riding a bike, I would have hit a tree [one of my childhood bike experiences] I had forgotten most of what I had learned. Since I had had two diasterous attempts back home trying to get my slower 40 into the air, this would be my first trip around the pylon in 2 years and perhaps my 10th trip in my lifetime. Needless to say, I was a little concerned. Practice, or lack of it! Shucks, I was not ready. But I didn't drive 10 hours to watch, so before I knew it, I was in the pylon, chasing my airplane. I'm proud to say it turned 145 mph, within, one mph of it's last flight two years ago, same prop and plug too! I, however, had changed. I'm fatter and slower. I got into a "SLUGGER BROWN" sidestep, I think the pylon was too low and when I last saw the airplane, it was diaappearing over my right shoulder [I go clockwise]. I heard it hit the ground.
I was actually laughing! The airplane was repairable, just a couple of cracks, THE PROP [more on that later] and a new landing gear. Glen Lee handed me a gear, Tommy mounted it his shop that night and next day I raised the pylon, made sure my feet stayed on the same side of the pylon and got a "standard landing".
"PRACTICE", how, important is that word?
I've been thinking about all the things that happened at Cinti...
I've never been prepared for a contest, this was no exception. I threw a bunch of stuff in the car thursday night, worked til 6 on Friday and started driving at about 6:15. I made it past Columbus by 2am, stayed in a dive, got up and got to the site by 8am. I was one of the first guys there. The action really didn't get going 'til 10am. I parked next to Tom Brown, I knew it would be a learning opportunity for me.
Jet Bill was good enough to mentor me though Sport jet testing. I got a lot of flights in. Saturday night, with jet pretty much in the bag, Jet Bill, Mike Couts, Paul Zurowski and myself hung around after the officials left and played with Jets. JB flew his "tin" upright and we all took some flights. That was more fun than what happened next day. JB dialed in my Sportster and we went to sign up. I took the circle, took off and not knowing the rules, stayed out of the pylon for a lap or two. I got into the pylon but could not steady the airplane. I got out and flew the attempt out.
I couldn't understand how I couldn't control the airplane. I took another flight, tried to give it "down" on the down side [I did what I was told] as it was again hunting badly and landed "below the deck". The airplane was fine but the severe ground contact bent the pipe.
Dave Cotton came to the rescue with his pipe straightener but I was done for the day .I did get another 40 flight in earlier, but with a borrowed prop I only did 141.
I am slightly mystified by my lack of control in Sport Jet. I do have a flat bottom airfoil in the center section. Doc always said that was a no no...I'm fatter and slower, but I flew the 40. [It too has a flatbottom center section, flys great when I can keep up with it] I think the jet is slightly tail heavy.
When I was riding home, I took the 40, rolled down the window and held the airplane in the airstream. Holding it behind the wing, I could not keep it from hunting with very little attack angle. When I held it in front of the wing, it "flew" very stable. It was easy to see the effect of CG. I hope whoever saw me didn't think I was a nut. I did the same with the Jet and was satisfied that I could go home and make some minor adjustments to it to improve me performance.
WE shall see...'til next time
I spoke with Lenny Waltemathe last night...I called to ask him about his JET secrets.
He told me that he builds basic sidewinders, very clean, out of basswood. He told me to read and re-read DOC DAVIS' articles in Speed Times and listen to Earl Bailey.
He told me to work systematically and with a professional demeanor, write everything down. He said that the goal is to get my stuff to work every time, predictabily, then try to make it go fast.
He feels that HIS current practice of entering 3 ships in one meet is especially helpful since he can focus on one ship and experiment on the others, but he is very mindful of keeping the ships consistent with each other so that he can MEASURE the effects of each change he makes.
I felt a little sheepish when he told me he has no place to practice and basically uses the meets to test [another reason to enter 3 ships] I've often complained about a lack of places to fly and people to fly with...
Amazing, isn't it? I'm sure that he has plenty of tricks, but no matter who I've talked to that is fast, the story is the same, work at it, do it the right way, be consistent and you will succeed.
THANKS LENNY!
The C/L Speed community lost a great member, our good friend Gordon Thomas has passed on. He struggled with health issues these past few years. He was a great jet competitor and held the Eastern Regional record for some time on the old line size. I for one will miss him.
As I've said before, I am an old magazine addict.
Well, I was peruesing one old mag, the article in question was talking about gliders and drag, explaining that elliptical shaped wings minimize the effects of wing tip vortices [drag]. This fella stated in so many words that tips that diminish to zero are more efficient. [I buy this, Ned says it EVERY time I speak to him]
The writer also says that the wing to fuselage joint is an irritating source of drag. [I buy this also, it was stated several times in celebration of the advantages gained by using an assymmetrical layout, although I am now convinced that the biggest advantage in terms of drag is covering wire]
Anyway, this fellow states that one way to avoid a wing/fuse junction
is to mount the wing on top [or on the bottom of the fuse?], so that air flowing along the length of the wing does not hit the fuse...at least one half of the wing [top or bottom] has it's entire span uninterupted by the fuselage.
Two examples of this are the HOYT SIDEWINDER, with it's wing mounted on top of the fuselage and the LAMBERT SNAKE, with it's wing mounted on top and possessing a long fuselage with a short engine cowl, so that the top of the wing is essentially exposed...
I also remember someone commenting that one of the unitentional benefits derived from the P-51 Mustang was that it's underwing cooling scoop was located below and at the trailing edge of it's wing. this arrangement helps to direct the vortices coming from the topside wing/fuse junction...
Comments?
Wings fascinate me, shapes, sizes, airfoils and how they work with various moment arms is something I never tire of thinking about.
For instance [and I must stress that this is just my opinion] I am not a proponent of symmetrical airfoils, not because I think that they are slower, but that I think flat bottom and Clark Y foils are easier to build. I think that a high wing airplane with a flat bottom foil may need to be nose heavy to
fly right, or have a lifting stab.
I think a mid-wing or low wing airplane with a flat airfoil will fly nicely. To my knowledge, a symmetrical foil requires more positive incidence or angle of attack than a flat bottom foil.
I've been very interested in yaw and what it does to C/L airplanes, consequently, I've written quite a bit about line drag and rake, but consider this...a C/L tail dragger, like a proto or an F-40, when on a takeoff roll, is moving in one direction [forward] while pointing in another direction [pitched nose up]
This means that a counter-clockwise flyer with a standard rotation engine, during take-off, has the outboard prop blade at a MUCH HIGHER effective pitch than the inboard prop blade [that is, when the prop is horizontal]
Now, when that prop is spinning at 36k or so [NOVAROSSI, anyone?] does this mean that there is a precession-like effect that forces the airplane to nose in toward the center of the circle?
Is this why a sub-rudder is so effective in preventing such behavior? By raising the tail, do we also "even out" the effect of the prop blades?
Is this also why clock-wise flyers are so much more better behaved?
Inquiring minds want to know!
Get some 3/4" plywood, cabinet grade [the good stuff]
cut a piece about 6"x12", this will be the base of the jig.
A DARP/Tippet D pan is about 1 1/2" deep, so cut some additional 3/4" strips about an inch wide and stack them lengthwise, THREE DEEP on your base and far enough apart to fit a D pan, about three inches, so that what you get looks like a mitre box or a channel, about
2 1/4" x 3". You will need the extra depth to be able to drive wedges under the pan.
take three hardwood strips, 3/4" square will do, and lay them across the top of your channel, one about halfway and the other 2 about 1/4 of the way on respective ends so that you are looking at four equally spaced "chambers", then drill and carridge bolt the whole thing together.
You now have your jig.
Here is how I use it.
Flatten the top of your pan. I use a flat autobody rasp, then dress it up with sandpaper on a piece of plate glass. Buy some of that blue stuff that machinists use, layout fluid is what I think it's called. Put some on the pan top surface and carefully work that surface till the blue is gone.
Slide the pan into the the jig channel and use wooden wedges under the pan to hold it up against the cross pieces, tap the wedges in to hold the pan tight.
Rather than use full length sides, my 1st jig used several pairs of short strips so that I could wedge support in several places along the length of the pan. I made a smaller jig for 1/2a pans.
You can now drill the pan. Be careful when you drill that the pan sides do not flex, especially COX TD pans. The jig I'm building now will have the channel sides tapered from front to rear so that I can wedge the pan in top and sides, it will support the pan from spreading. Be sure to leave enough room for a rear wedge to fit into the jig.
I try to figure out where all the ALL the holes must go and drill/tap them before I start to remove pan boss material. You must definitely thin DARP pans or you will have a HEAVY airplane. I use 5 hold down holes, two ahead of the engine. I do not drill the hold down holes that go through the wing till after I determine where the wing will be. I build the fuselage, add the engine, stab and all the trimmings, tack it all together with a dab or two of CA and rubber bands, determine a C/G, then build the wing, place it, take the whole thing apart, then drill those remaining hold down holes. This way I keep the hold down holes close to or near the control wire. Don't leave anything out. That length of pushrod wire will DEFINITELY change the balance, so will that prop and tailskid.
Buy a drill press, they are worth the money. I have a Buffalo [cheap import], it was given to me but new it was around $100. If you look in those WANT AD magazines, you'll find one cheap. You can use a hand drill if someone will use a triangle to keep you going in straight. I use my drill press for lots of things and all my profile airplanes benefitted from straight true holes. Between my drill press and my belt drive table saw, I have been able to build lots of airplanes...
2-56 taps use a #50 drill bit .070"
4-40's use a #43 .089"
6-32's use a #35 .110"
Buy two of each tap, use one tap to start holes and take the other tap, Dremel the tip off with a cutting wheel and use it as a bottoming tap.
De-burr it on a grinder BEFORE you use it and TEST it before you touch the pan with it!
Use the right bits and taps, no sense breaking a $4.00 bit or tap in a $30.00 pan. Use good bits and taps. Use cutting oil, anything will work. I use motor oil. "Measure twice, cut once" is an adage an old carpenter taught me. USE a prick punch to make sure you are not drifting as you drill.
The pan is the airplane, so spend the time to do it right.
Well, now that we have a new group of NASS officials, perhaps there will be some different approach to the "problem" of new participants...I do not think that a new class or participation according to skill level will increase participants, but I do think that several steps could be undertaken.
Just thinking out loud...
I have basically wasted several flying seasons by getting a new jobs, moving, unpacking and searching for sites and flying partners. While I have been sucessful finding a sites and partners, the sites are sometimes unfortunately...grass.
But as many may know, grass is not conducive to speed models. When they land, they tumble...unless you can get them to land SLOWLY.
I got into a discussion on the Delphi site and John Bruman mentioned that he and Chris [his grandson] fly SKAT RATS off of grass. That was a clue that smallish, solid wing craft can land on grass. John mentioned that the skat had 150 square inches of wing.
I decided to build a large profile powered by a Super Tigre X-60, not a great engine, but good for this project. I built my standard flatbottom center section to washed out tips wing, balanced it at 45% with a 40 % stab. U-control.
It flew fine, the engine needs some more time, but it landed SLOWLY. I think that a .65 powered airplane with a little more wing area will be good enough to fly off grass and actually be fast enough to simulate a speed ship...maybe even be competitive?
When I first started this page, I had a very narrow viewpoint on the venerable and time tested practice of using various latex products as a
method of delivering fuel under pressure to our thirsty little monsters, the two stroke glow engines...
The 2000 nats [seems like years] found me with a new airplane and at the mercy of such a system. I had planned on using a hemostat as a Q&D shutoff device so as not to disturb the needle setting on every flight, but alas,
that was way to unwieldy for even a veteran like DAVE MARK to use, so we elected to use the NVA as a shutoff.
I am firmly convinced that a bladder still has it's place in speed flying, both thru my experience in 2000 and from comments made by the 2001 nats F-40 winner, GLEN LEE.
Glen uses a bladder on both his 40 and his .21 proto. He contends that in the "DRAG RACE" events, the bladder system delivers a more consistent volume thru acceleration to top speed phase than a hard tank, thereby
allowing for a slightly leaner setting on the ground [more power] Since the first lap is the slowest, you would want a peak power delivery from the start. I think most would agree that a bladder is the most consistent fuel system
and is the system least effected by gravity etc.
I can't argue the merits of bladders in this application except to say that I agree with Glen based on my own limited experience.
[PS, none of this was told to me personally by Glen but was related to me by someone who had a conversation with him...]
As well as bladders apparently perform, they have been problematic [now that I'm a CORNELLIAN I get to talk like that] in the following:
The first problem can easily be controlled in any number of ways but I recommend and have already used a FUEL shutoff device, any of the following methods can be used:
Glen Lee, as reported to me, uses a form of 1/4 turn shutoff, as is popular with our bretheren, the FREEFLIGHTERS.
Having used a system similar to this, I can report that this is probably the way to go.
The second problem is a little more sinister [ha!], that is, breaking a bladder on the circle and almost assuring a lost attempt.
Dave Mark and I were discussing this and I recalled seeing Frank Garzon go 190 on his first D attempt [at my first NATS] and then proceed to POP bladders on the circle in three subsequent attempts.
As we were discussing this, Dave mentioned that Glen Lee used two hard tanks in his B SPEED, one on pipe pressure to start out, then finishing on a suction tank.
It dawned on us that perhaps putting TWO BLADDERS into an airplane, one filled and one "just in case" may have some merit.
A bladder weighs next to nothing and takes up little space when empty, it would be a simple matter of devising a way to switch lines...not too difficult, if you know how bladders are filled from the outside of the airplane.
Just a little "food for thought". I think that a bladder system as described would be as reliable as possible and probably be just as sucessful as a hard tank in any non-piped application.
Callum, from our message board, provided us with a link that discusses engine cooling in a team racer. I notice that many F2A ships have various inlet scoops. Perhaps this will help to explain why.
Are you hankering to get a pulse jet?
Before you buy anything, get the JET-PACK reprint package from MIKE HAZEL of ZZPROP. It contains some great information about JET-SPEED.
If you want to see some different ideas on speed
For a look at plans for a few famous and not so famous speed ships that will help to illustrate some of the characteristics that are described in the text, including the outrageous ROSSI brothers jet.
For an explanation of P-FACTOR and PRECESSION SEE BOLLYand scroll to "DYNAMIC FORCES" in the propeller section.
For a better explanation go to Denker's SEE HOW IT FLIES
To down load a program to calculate line rake
This link is by Peter Soule.[thanks to Bill Stewart]
John- Some hints on using Pete's line rake program-
- It was written for F2C airplanes, so it has some features not necessary when flying from a pylon.
- Set handle radius to 0.00 ft
- handle angle to 0.0 deg.
- temperature to anticipated, deg. F
- Airspeed to ft/sec (MPH * 1.467)
The program was written for two lines; to solve for monoline,
- simply enter twice airplane weight
- divide the results obtained for Tension and Power in half.
When you are familiar with the program, it is possible to solve for whipping power ( which can be substantial with Monoline). Bill Stewart
Check out the 1950's MIT study on LINE DRAG.
Go to the MESSAGE BOARD and download Bob Fogg's program on line rake calculations. It is under general dicussion, message #116.1.
I love this thing...
Hello John,
I have been following the discussion on the forum about what event to start
with and I thought I would send you my idea.
First if you want to gain
flight experence, dont plan on jet supplying it. I have been back at
contest flying now for four years and have noticed that most jet flight
attempts are just that attempts. The experts from Texas make it look easy,
but they have been at it for 25 years. Just jet. That is it, JET, to get to
the level they are at today. A rough road for a newbe.
You will get many more completed flights with F-40 or 21 Sport or even
proto. If you decide to build a F-40 buy a set of plans from Ned Morris
for the Indy 40. They are $8.00 plus shipping. Study them. There is a
great amount of information in that set of plans.
If you build a pinklady 40 do not build it inverted! Make it a upright and
use info from Neds plan to set it up.
Till later,
Dave Mark
BUT DAVE, I LIKE JET!
Dave volunteered to help me with my F-40, As we discussed progress, some other subjects came up.
Dave shared some insights on Sub rudders and THE FIRST LAP of a F-40.
I have a belief [shared by others] that a sub-rudder should be used on planes that fly COUNTER clockwise only. The reason for this is that on a clockwise ship, the spiral wash from the prop at low [take off] speeds will effect the sub rudder so that the airplane will tend to turn into the circle.Dave suggested that regardless of the direction of flight, a SUB-RUDDER should be used for a very different reason.
Dave went on to explain that while a sub-rudder will indeed be effected by spiral wash [as will the wings, cowl, stab, etc.] The best purpose of a sub-rudder is to elevate the tail of an F-40 during the take-off roll so as to keep the angle of attack on take off from being too steep. His observation is that when a 40 takes off tail down, it is slower. The angle on take off forces the pilot to input a directional change [trim down elevator] which scrubs speed. He has even witnessed near wingovers.
He feels that the sub rudder allows a pilot to find the groove more quickly.As you all may know, F-40 is timed PROTO. That is, the timing starts on release. This event requires much more SYNERGY [like that Ralph?] between plane and pilot than other events.
One example of this synergy is illustrated in an observation made by Dave and Barry Tippet.
They used some calculations to determine that if a 40 pilot whips his model into the air at arms length, he might be ADDING up to 85 FEET to the first lap, depending on how long the whip is!!! This occurs at the slowest point of the timing, takeoff.The net effect is obvious, if your airplane must fly the longest lap at it's slowest speed because of too much whipping and if you must spend the first lap trying to level off because of too steep a takeoff angle, you are gonna have a tough time being consistent [and fast]!
Dave believes that your airplane must roll and takeoff low and straight, with as little yaw as possible. He wants his pilot in the pylon ASAP to MINIMIZE the circumference of the first lap.
My personal observations of Dave's 40 program lead me to believe that Dave has throughly researched anything he is doing, so it may be worth your while to consider what he says. His stuff goes!
The latest from Glen on BALANCE.
Todd: What the others are saying about the balance is true. If you just copy the stock dimensions of the counterweight you'll be in the ballpark.
If you want to get fussier, and allow for the port being moved, balance on a "wheel" type balancer. This can even help on a stock type crank. (see some of the Russian engines, .15 size for examples). The amount of counterbalance needs to be in the 50~65% range of the weight of the piston,wrist-pin,(ring, if used) and 1/2 the weight of the rod. To test this, measure the weight of the reciprocating parts on a good gram scale, and make up bob-weights in this amount to add to the crankpin, before you put it on the balancer.The crankpin should "stop" at the 12 O'clock position. On a single cylinder engine: If you add weight to the counterbalance, or lighten the reciprocating weight. you DECREASE the PRIMARY shaking imbalance (vertical= Cyl. bore axis), and INCREASE the SECONDARY imbalance (crosswise= across the lugs).
For this reason, IT'S IMPOSSIBLE to balance a single Cylinder engine, without a secondary Balance shaft, as used in some auto engines. Adding weights (heavy slugs) to the counterbalance is done to change the resonant frequency at which you get a "Harmonic" or strong vibration level. You want this at a lower than full rpm number. Most of the ST X-40's used in Formula-1 Pylon and Fast Rat had cranks that needed this changed to resonate in the high-teens (RPM). Sometimes you could see the engine "shake" in this range, on the test stand. I never put a strobe light on one to see what one would look like while running. If the engine is balanced to "resonate" at full RPM, IT USUALLY COMES APART. This has been known to happen in full size auto racing engines in the past, with the usual DISASTEROUS RESULTS. Valve springs on auto (4-Cycle) engines can do the same thing, with the same results.The timing is MUCH more critical. Try 35~40 deg. ABDC opening, and 65~70 deg. ATDC closing and you won't be far wrong. Also remember to use at least a 1/16" radius in the corners of the port, and @ .020+ minimum wall thickness on the port edges, with a smooth surface finish, before heat-treat and finish grinding. Use the maximum corner radius for the size bearings being used. ( the "inside" corner where the front and rear bearings seat against the crank shoulders.
Finish the crank to the "right" O.D. dimensions. I like to use minus .0001~.0003' under the nominal ID dimension. (.5000, .3750, .5906 , .2756, whatever) MINUS the above amount. Henry fits his tighter than this(especially the rear Brg.), and uses an "extra loose" clearance in the bearing to compensate. This makes sense if you want really long life from your engines. (ie: Rat, Pylon, etc.) All for now. Cheers, Glen
I recently spoke with Glen Dye, ordered some nva's and asked him to check out the Review. Here is Glen on...
John : I received you order/letter yesterday. There may be a problem with the mounting position you show on your letter. The NV is usually mounted so as to get the needle in a horizontal position ON the pan C/Line. In your sketch it would have to come out the top of the pan. This would still work, as allmost all the F1 Pylon racers had theirs coming out a similar location.
I've seen Dubby's Backplate B-4, and like it better than Henry's because it has o round "venturi" section in the middle. You want to inject the fuel just slightly downstream of the smallest X-section area. the alternative is to use a remote mount for the NVA and just put a K & B nipple in the venturii where it needs to go. Center drill, #21 drill, 10-32 tap, and spot face are whats required.To change the subject: 1) Source for vacuum pumps: APACHE RECLAMATION AND ELECTRONCS, 313 W Apache ST, Phoenix,AZ 85003 Ph. 602-254-0613 I don't remember the prices, but they had a couple of pallets of them of different sizes when I was there @ 6 weeks ago. It 's also a GREAT place to scrounge for the the unusual industrial surplus. It is Just north of I-17 between Central Ave. and 7th St. This is just south of downtown Phoenix a few blocks. I took Steve Eichenberger there last summer. They are in the process if doubling the size of the place. When the last of the slum houses are gone it will be @ 4 or 5 (small ) blocks in size! their prices are usually very reasonable. Brian Seegers told me about it 10 or more years ago, and I stop by every time I'm in Phoenix.
2) Piston and sleeve fit is the Most important thing you can work on in an engine!!!!!!!!!!!!!!!!!! If everything else is right; The better you sleeve and piston fits the faster you'll go. If you only have an " average" sleeve and piston, you'll only have an "average " engine. Change to an Excellent sleeve and piston and you'll have an Excellent engine!!!!!!!!!!!! Props are equally important!!!!! Unfortunately, for the average modeler, almost anyone can work on props and with diligence get results. The same is NOT true with sleeve and piston fits however. Most modellers should leave the fit alone !!!! If you only change ONE thing at a time,and keep track of the changes AND ARE METICULOUS ( See Carl Dodges' engines ) you MIGHT be able to improve on the "average" fit . (NOT Henry's though ) It takes LOTS of skill ,Patience, Machinery and time to do an Excellent job. There are exceptions: I personally don't agree with what Neddy does, but He goes faster than I do because he works on his PERSONAL stuff FIRST ! I was always too busy working on customer parts to find time to get my own stuff in first class condition. ( I STILL am burnt out on models! ) Neddy also forgets that prior to the 89 Nats ; He spent a week here with me working on HIS Stuff, and Not leaving me any time to get mine ready. I think He and Joey got the high point trophy that year. Bob Fogg and Slugger are also working HARD on their stuff and consequently set records. The late Bill Nusz was also a GREAT competitor this way. Look at who is going fast, and ASK them; Most of the modellers today will talk to you and tell you what you want to know. Not like in the OLD DAYS when everything is a big secret.
3) Are you running the high timing sleeve in your GRRT ? [good question] The one I bought from Carlson last month (# 3065) has ridiculously high timing. With another sleeve with @ 162~ 165 Degrees of exhaust is what you should be looking for. The trs. want to be @ 130+ . A good Nelson clone head insert and a 1" exhaust would make a fairly good engine for starters (@ 150~155 ) . There is a newer Nelson clone (#3070 ) with 6 head screws and a pie shaped backplate that will soon be available, but prob. not as cheap as the $150 of the 3065. Too bad they didn't copy the FR Nelson !! It is at least 5 MPH faster than the RR. I have 2 new 3065's and 2 used Nelson RR's for sale.
There are still lots of good obsolete F1 ST X-40's out there for cheap, and even more RR Nelson RR F-1's since they no longer fly F-1 PYLON OR Fast Rat. There could be a BIG entry in F-40 next year !!!!!!4) Bill's sub -rudder does work very well on a CCW flying model. Too bad He's not still with us !!!!
5) I have hanging over the fireplace ,probably the LAST AQUARIUS ever built. Nick Sher built it in 1976 for the Dayton Nats with a piped TWA .29,but never flew it. We won that year with another similarly powered model in light rain. If it hadn't been raining we wouldn't have been nearly as fast because it would have overheated. Nick's Proto would have blown us away if he had chosen to fly it. The Good results Team Brown had at the '90 Nats were mostly due to their purchase of most of Nick's models and engines the previous winter. Very few modelers give credit where it is due.
Bill Nusz built the models I have now, and Jimmy's record holding F-40 , plus lots of others for various people. Not very many of them were ever put to good use. Jim Clary has 2 good S 21-s that I sold him 2 years ago ( 1 Nick Sher / Picco and a Paul White/ NR-21 ). I'll bet he hasn't even run the engines. Likewise, my flying partner, has a very nice Ironsides he got from Lenny W. in April 98 @ Whittier Narrows BILL NUSZ MEMORIAL #2. I don't think he's even tried to fly it nore than once or twice !!!! So much for old age !
A recent correspondence from Glen
I'll try and go thru this in order: O S .65s: No, there aren't any more O S Spinners/Drive spools available. You can make one or buy Henry's or Slugger's ( George Brown , Tempe Machine, Advert in Speed Times). Marty has been making his own. Try Marty at: customcom@wolsi.com .
John Newton has a glass top for a D that goes well. He's working on a new B for me that I hope to have for the next contest in March?? He will also build you a complete model if you'd rather not do it yourself, but they are expensive.
For A: Go to Thomas Mejzlik's link on the Delphi web page and order one of his F2A ships for $200. and then send it Jerry Rocha to change over to monoline for you. The PROFI Jr. engine is a good bang for the buck, unless you want to chase the record. Then spring for the Regular Profi 2.5cc @ $470.+ shipping. If you're not wanting to spend as much or go slower, you can get an Irvine (std/old-Pipe model) cheap or get a Picco .15 for under @ $100. The GOOD IRVINE.15 (Hallman Spl) is @ $400. and it's almost as good as the Profi.
OS.65 Mods: 1) Port & chrome Sleeve & fit piston @ $50~75. 2) Cyl head for Nelson Plug (1pc. double-bubble) $ 45. ( Needs to be fit to sleeve after plating) 3) Big Mini-Pipe/ Exh adapter @ $30~45. Bob Fogg makes one like on his record ship for $42. 4) Retime and rebalance rotor,and prep. @ $40++ Henry Nelson is making some new parts for this motor: Rotors & backplates(?) AAC Piston & Sleeves ( New Style,Big OD) so you can give him a call on those. 5) I personally like longer screws in the case and the 6001 rear bearing mod with at least the good Boca plastic cage bearings ( ceramic optional + $40.) I also used to modify the cranks and flash chrome them. 6) A venturi/ NVA will cost you $25. I DON'T have ANY pistons for this size engine anymore, and have been unable to get any, BUT now that Randy has bought K & B , maybe things will change.
I'm Not really looking for any more work, but you're an old friend and I would do your engines if you wanted.George Brown and Tim Gillot also do engines. Timmy is VERY expensive!!! ( and Slow) But then so am I (Slow) "It now takes a WEEK what I used to get done in a DAY!"
The X-40's also need to be looked at and freshened and possibly a straight Exh. stub for a 1" mimi-pipe. They should both be the 1PC Case model. Slugger makes both a 1-1/4 & 1-1/2" spinner that will fit on the ST collet and you need to decide which you're going to use B-4 doing the pan. I did the ST's with pretty much the same prep as the OS, plus the ST needs the case prepped, but that should already be done. If the Shadel Engine has grooves on the piston, I probably already did that! ( hopefully they're both in good shape) All the above is based on NEW OR NEAR NEW PARTS!!!!
Jimmy R. is talking about using a Picco.15 in an asmy. A job as the Late Bill Nusz has one @ 10 years ago that had Great potential, but never had the problems sorted out. Jimmy also was going to do an article on his Bill Nusz, Record holding F40. I think he's got the drawings on Cad at work, he just never got around to doing the rest of the article. It was going to be a small tribute to Bill. I sure miss him, and Larry also. Both the D and F40 I have that Bill built are EXcellent flyers!!! Jimmys' is not as good, but faster. He's retired it after the pan cracked at the last 3 contests. Nelsons (FR) vibrate a lot!!
I just thought of another mod for the ST's: If your sleeves and pistons are shot, get AAC ones from Henry. I've done a couple of them like this ( 1" OD) and it works better than the stock setup. VERY close to Nelson performance actually! Cost of the instalation is @ $30~45. You should have a Nelson plug head ( won't go in a short reach head) .
I'm going to have to try a speech recognition program, as I'm TOO SLOW A TYPER (Dragon?). If you need any phone #'s on the above, please get back to me. Most of them should be in the Speed Times Listing ( Chris Sackett $ 25 ?? ) Most any speed engine will need the above treatment; Except for the .21's, and the Nelson's, which almost all need the Cyl's U milled to fit in a decent sized cowl.
Almost any of the "better quality engines will work, " IF THE EXHAUST PORT ISN'T TOO HIGH" (Pipe timed!) Some are just a lot more work than others, and past a certain point, it cheaper to buy something thats' made right to begin with!!!!!!!!!! ( Nelson,Profi, Hallman) All for now; Cheers, Glen

Eddie: The material you have from Germany SOUNDS like the Mahle 244 ( @25% SI). Henry used it at first @ 10~12 years ago. It has several problems:
IF you remember to CAREFULLY break the parts in the First couple of runs. Otherwise they SEIZE and score, and you start over!! This is the same surface finish that was used on the Chevy VEGA engine block back in the 70's. They developed a special honing process to hone the cylinder bores, HONING THE ALUMINUM, AND LEAVING THE SILICON PARTICLES for a hard wear surface. When you get those "SHINY pistons (ie. Henry's) this is the REVERSE of what you want!! DULL, DULL, DULL, AND ROUND.
If you can't get the sleeve and piston to .0001 TIR; (or better yet .00005) ; WITH THE RIGHT TAPER ON THE I D, GET SOMEONE ELSE TO DO IT WHO CAN!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! See my list from a couple of days ago on the Delphi forum: azpropnut= Bob Christ This is where the HP is at!!! ( Assuming you've got everything else somewhere in the ballpark). The "Diesel truck Piston alloy" of old was only @ 11~13 % SI. I would hope that you've at least got some newer alloy like Reynold's 390 (17~19% SI), which is the minimum you need for a good hard, long-wearing piston. 393 would be better (21~23% SI) Otherwise use it for Sleeve blanks and get Henry to Chrome it for you. You need to find both a sleeve and a piston material that are compatable for expansion ratios. There are almost endless choices here, and that is why I suggested getting material from Henry. His works!!!
K & B's alloys also work, but getting parts from Randy right now is next to impossible. He's still setting up all the K & B Stuff he bought and then moved back to L A in the last two months. You might be better cutting up the pistons into strips, and then turning them round, and then making bar stock pistons. Carl Dodge did this years ago with a Hi-Silicon diesel truck piston forging blank from work. It took forever, but he got a lifetime supply of .15 pistons! Frank Garzon played with casting pistons from old VEGA blocks etc. back in the late 70's and early 80's. Unless you're good at casting Hyper-Eutectic (Piston) alloys, you're biting off a lot!! Here again, I'd recommend BUYING something that WORKS, at least to begin with. Then, if you want to expirement with your "OWN" setup, you'll have something GOOD to compare it with, and maybe won't get so frustrated with something that does't go FAST enough. Remember: This is a LOT of NEW things you will have to master in order to make a good runing FAST engine!!! All for now, Cheers, Glen PS: You need some cyl. head fins and a thicker front hsng. flange, and IX-nay on the Fox plug! Use Henry's!! It's faster!!!!
I asked Dave Rolley about his latest projects and it he reported that he is making 1/2a PROTO wings using blue foam and glass/carbon, then vacuum bagging.
Ned (and others) think you need a vacuum system that will pull to almost nothing. I'm using a system here that easily goes to 18" of mercury. It is just fine. Depending on my setup, I can squeeze out so much resin that the part is too "dry". Depending on the foam, I can crush it flat.Other than making tooling (molds), I don't need any more than what I have. I can always use Greg's [Settle's] "killer" pump if I really need it. (or I can order a different vacuum switch from Aerospace Composites for my setup which will let me get to 24")
I got the $250 starter kit from Aerospace Compsites. It had everything I needed (pump, accumulator, vacuum switch, mylar, breather cloth, peel ply, bagging material, clamps) except the foam, cloth, and resin.
You can build a better setup, but not without spending a lot more in either time or money. Once you have a setup, you can get most everything you need at a local boat or race card fiberglass shop. Even some rather exotic stuff. One shop here has a carbon/kevlar weave with carbon on one axis and the kelvar on the other. It would look real neat on a wing, but it is 12 oz per yard (heavy!!). But the black and yellow looks real good.
The wings I'm working on right now are "proof of concept". I have the foam cutting down to where I can cut the Dow "Blue" styrofoam with NACA 14x0 airfoils at a thickness of 3/16" without ripples or burnouts.
I have successfully vacuum bagged one of the wings and was pleased with it as far as I went. My next set is to make the tooling to do wings for our next 1/2A Profile Proto. My old design used a 24" span (which I really like the looks of), Dave Jr's model at the NATS had an 18" span which looked OK. I'm thinking about a 15" span wing. But I'll probably stay with 18" span. At that span the root chord will be 3" and the tip will be 2.125" for 46 sq in total area.My plan is to use 3 layers of cloth. Starting next to the foam with unidirectional carbon fiber running tip to tip, topped by a layer for 2 oz glass cloth, which is in turn topped by 3/4 oz glass cloth. I am still debating the necessity for a spar in the foam. So I'll probably make up at least 2 wings in the first batch (maybe more) and see how I feel after I break a few playing with them. Then I've got to get some in a couple of models. Perhaps we will build some testbeds when Dave is home at Thanksgiving.
None of the small foam wings have made it into a model yet. I keep playing with them til I break them. But the new ones are a lot tougher than my first attempts.
I did a goodyear wing out of the blue foam. 3/8" thick and vacuum bagged 1/64" plywood as the covering. (1/64" ply weighs about the same a 1/16" balsa) You almost can't flex the thing. Since I used 1.5 pound per cubic foot foam it is really light. The fuselage and tail are built so that should be ready to test before Christmas.
Composites are not hard, just messy. It is a lot like welding. All the time goes into the prep and setup. The actual work (on small stuff) goes rather quickly. But it is messy. Don't try it on your wife's dinning room table! (there is a little voice of experience in that comment :):) )
Later
Dave
I had a conversation with a relatively new but very successful speed flyer the other day. Strangely enough, the subject of speed flying came up.
Here is what he had to say:
I think the two most important details in speed are;
- proper fit between piston and sleeve
- proper propellor prep
If you can lap your sleeve so that you relieve the piston fit at the bottom of the stroke and keep a tight fit at the top, you'll have more power. This is best accomplished with a tapered lap. this is of course a very general description of what you have to do in order to get a good fit. I'm just trying to offer an opinion on what this flyer feels is important
If you can get both prop blades to pitch the same at mid station BEFORE you begin to carve, you will have an easier and better quality modification. This is done by trueing the hub before carving the blades.
This flyer feels that timing, breathing, head shims and other engine modifications do not effect performance nearly as much as fit and prop.
Along these same lines, Ralph Lindsay has these comments about engine design:
...Ira Hassad in the 40's designed his Sky Devil .65 with rear transfer ports and front exhaust so the uneven pressures on the piston would be radially perpendicular to the wrist pin axis and would tend to minimize piston cocking. He found that the back to front configuration as opposed to the conventional side to side showed a considerable improvement in RPM and HP with a noted (measured) reduction in engine temperature and a substantial improvement in engine longevity even at these higher performance levels. I wonder how much this effect has on the new rear exhaust, schnurle ported (symetrically ported) engines of today. Seems to me that the same benefits would apply. Maybe the "tuned pipe" is getting the credit due to this advantage.. Just a passing thought. I discussed this with Bill [STEWART?], as he had a Sky Devil and was very much impressed with performance that exceeded the "Hornets" and "Doolings" of those days.
This was the same engine I used in my assymetrical job in the 40's[the one that shot down the HELLCAT]. The only difference was mine had a 1 in. dia. shaft (the Edco version had either a 13/16 or 7/8 in. shaft).
Another attempt to attain the 7th level of awareness.
This was taken from Martin Hepperle's page.
The serious pylon racer[Boo!] needs to know about the power output of his engine. It does not matter whether he mechanically modifies the engine, or just performs the final tuning by adjusting the compression ratio and the length of the tuned pipe, or by selecting the best glow plug. In general it is not necessary to know the power output of the engine exactly in Watt or h.p.; instead, it is sufficient to compare the rotational speed with a known propeller.[get a bench prop from ZZPROP, see parts page]Comparing the r.p.m. values for different engine adjustments should lead to the maximum power output. It might be interesting, that the power to turn a propeller depends on the rotational speed to the power of 3.
This means, that an increase in speed from 20000 1/min to 20500 1/min corresponds to a power increase of (20500/20000)3 - 1.0 = 0.077 which means 7.7 % more power. Achieving the same difference of 500 1/min at a base speed of 25000 1/min results in a power increase of (25500/25000)3 - 1.0 = 0.061 which corresponds to 6.1 % of the initial power. We also know, that the power required to pull the model through the air depends on the speed of the model to the power of 3Thus the above power increase of 6.1 % could lead to a speed increase , which means 2 % more speed.
Interesting?
I had a chance to speak with Mike about the plane. It is a SMALLISH sidewinder. It has ellipitical wings and an elliptical inboard 1/2 stab [Mike cut off the out board 1/2 recently, explaining that he was tired of it burning from tailpipe proximity] The plane was built several years ago and Mike said it was not very fast...at first.
The most distinctive feature of the airplane is it's wing. The outboard wing is mounted on top of the fuselage in a typical sidewinder style,about 3/4" above the thrust line. Mike has the inboard wing mounted on the thrust line of the engine. This allows the control wire and its attendant drag to be on the thrust line also. Mike explained that other SIDEWINDER JETS usually have to build positive incidence into the stab in order to compensate for the drag center. Upright jets usually have to trim in the opposite direction. These practices add drag. Mikes design allows him to set up 0/0.
Mike's airplane was also equipted with a new tailpipe design. Halfway back, the pipe expands to about from 1 1/4" to what looked like 1 3/4". I was told that this was an attempt to introduce more air during the tailpipe induction.
As stated elsewhere, it seems as though the sidewinder design is the best way to deliver fuel to a jet engine. Get a copy of the Hoyt Sidewinder construction article and the enclosed explanation may convince you too. The high wing design is a concern for trim. The Fiske design seems to fly better than a regular sidewinder. Check it out yourself.
For me, the mission of NATS 99 was to fly an official in the pylon. I bought a practice pylon and practiced as much as I could. Last year, at my first nats, I was too busy gawking to draw many conclusions.At the 2000 nats I was better able to observe what was actually happening.
One thing that I noticed was how well the Texas jet crew worked together. Another impressive moment came while watching Jet Bill and Mike Couts dial in their various airplanes. They seemed to know just what was needed, when it was needed and they knew when to stop fiddling.
However, when it was time to fly my SPORTY both they and several other flyers could not identify the reason why my jet was flaming out. Later it dawned on me that the reason all these fellas seemed to know what to do with their airplanes was that they were familiar with them. In other words, they practiced. They had an idea what was wrong but the lack of familiarity with my airplane prevented them from identifying the problem.
In football, a two hour game requires a massive amount of preparation. Players take years to develop. Coaches never expect anything to work in a game unless it worked in practice.
So it is with speed.
Bill Garner said that he was never suprised by the performance of his airplane. He knew what it was going to do. This knowledge was based on what it did in practice.
The team approach seems to be best. Look at all the father son teams. Look at the Texans. Morris and Mathison. Fogg and Brown.
This years nats left me with this plan. Find a crew to practice with and do it. All the equiptment in the world will do you no good if you don't know how to use it.
THE NATS FILE GOOD NEWS! After several quick lessons during lunch on NATS thursday, I was able to sucessfully launch my F-40 and get into the pylon. 4 consecutive flight's, two of which were official's. Many thanks to Barry, David and Frankie.
I feel as though I've come a long way in speed in the past year. [In the past months I've even come a long way with computers]. These were positive changes.
One subject that was a very big discussion on the message board is that of the lack of an "intro to speed" event. I waxed poetic about the demise of speed, the lack of mono-line pilots, the difficulty of the current events etc.
I've recently gotten hold of some old modeling magazines from the 40's, 50's and 60's. I was suprised to find these same topics being covered and lamented upon, things like dropping Jet speed, combining carrier with scale, banning monoline etc.
This nats taught me not to question or criticize until I know the facts.
Here is what I think at this time:
I now realize that the pylon can actually aid a pilot. Many pilots rely on the pylon as a support when flying ships that pull hard.
This nats, I watched the pilots, not the planes.
I was left with the impression that flying a D with U-control would be difficult at best. The hand that is in the pylon in U-control is also the hand that is doing the controlling. An airplane pulling at 90lbs could be a handful[heh-heh].
Monoline allows you to hook your thumb onto the pylon with one hand and control the plane with the other In fact several pilots, [including Santo Rizzoto, who is on the far side of 60 years old] told me that they much prefer monoline in the pylon than u-control.
Monoline flying is a skill that can be learned. I now believe that most of my problems [I don't have too many now] with monoline was my setup, not the system.
I now know that the FAI banned monoline not because it was too difficult, but cause it was too easy to WHIP! In fact, there was quite an effort to find a way to retain monoline by using reversed slide sticks and geared handles [picture page for examples]
These guys were going out of their way to include me in any way they could. The Van Sants, the Garzons, Jet Bill and Mike Couts all made sure that I got a chance to get close to the action [even after a screw up]. These guys would make great coaches!
The timing tent entourage gave me a standing ovation on my first [successful] official as a pilot. I was "lent" an $800 dollar airplane. Mike Fiske, Doc Davis and Dimmit Perkins each gave my sidewinder the "eye". Dimmit made sure to tell me to "stay with it" in jet. "POPS" Garzon gave me a reworked Kelly prop. Doug Gray gave me my MVVS GRRT!
My uncle taught me to swim by throwing me in the deep end of the pool. He didn't care how fast I swam, he knew I wanted to swim and he thought I was able. He knew I might could sink. But if I sunk, he could pull me out.
I now feel we don't need another newcomer event. No one cares how fast you go, what they want to see is your effort. Does your stuff work? Do you work at it?
Newcomers, just jump in, someone will help you out. Make no mistake about it, you need a mentor. Mine have been Doug Gray and Pete Kladios. Use the phone and the internet. I can't tell you how much help I've received from Ned Morris, Chris Sackett, Bill Garner and a dozen others.
So far, my accomplishments have been few, but not one of these fella's has ever discouraged me.
The nature of speed has made it evolve to what it is. Lots of clever people have spent lots of time and effort to get it this far. When they move on, there will be others to take there place. Speed, it is not easy, not for kids, not for those who won't work at it. But if you want to do it, you can.
I received an E-mail from Bill Stewart, current record holder for Class-B electric[114.75 mph].
"...C/L FAI[F2A] speed is impossibly fussy...sort of like F-1 racecars...there are two electric speed classes, A&B, which are wide open and generate much interest...To offer a comparison with conventional speed, A electric, which runs in the low 90's is like flying an old ARDEN or BANTAM .19; My B ship, line pull etc. is exactly like my McCOY .49 class C ... So investigate electric speed and see what speed used to be like...
Bill is looking for TORNADO or REV-UP 8-8's. His e-mail is gstewart@gte.net. I would like to try E-SPEED just because I could fly in a lot of sites where NOISE[shhh!] is a factor.
MORE ELECTRIC SPEED. Bill Stewart sent along more info on E-SPEED
"...with NI-CAD batteries, currents as high as 80 AMPS are not unusual...hardware problems involve handling this flow. The airplane must have some means of SWITCHING THE MOTOR ON AND OFF...the A-SPEED record holder uses a simple 30 amp automotive relay... off is [tripped] with full down elevator. Another approach had the relay latch itself until voltage dropped...at which time the relay opens. Another setup used FET's[?] in parallel to switch on/off etc. All this to cut power after timing the run so that the ship does not settle with the motor [still] running, for a 50,000 rpm no-prop catastrophe."...hand launching is not an option since power to weight ratio is too low...you can count on breaking a prop on every flight, since most motors windmill...those with strong magnetic rotor location have 6 stop positions... CLASS A, which is limited to 7 CELLS and a 30 oz. max weight...powered by ASTRO-FLITE FAI-05 motors with 4 or 5 turns... CLASS-B,30 ni-cads and 60 oz max weight...AVEOX brushless motors [Bill runs a 1415/2Y] and ASTRO-FLITE FAI 40's...my [his] fastest speed, 115 mph with 18 ni-cads. ..airplane has a 30" inboard wing, 30" fuselage...the next step is a CARBON FIBER fuselage to save weight for a larger battery... single or two blade WOOD props to protect the [armature] shart from bending...best speeds with 8/8's...
In flight these airplanes have a great sound...a turboprop whine...if anyone wants more info contact John or myself..."

do you wanna see an electric speedster?...thanks to Pete Soule for this photo and the following comment:
"...Record application sent in 121 mi/hr in electric B draws 70 amps (no nitro-no methanol) A shocking turn of speed..."
To which Bill Stewart replies:
Hi John- Pete Soule's photo actually shows Howard Doering's remarkable Class A record holder.This ship betters 90 MPH on only seven ni-cads.
Regards, Bill Stewart
Here is the latest from Bill and Howard concerning the E-SPEED WARS. This is a report from the latest contest in El Monte, CA.
In our E-Classes Howard Doering (A), and I (B) both came within one MPH of the existing records. The interesting item is that Howard flew from a hand launch- this used to be the normal way to fly speed, but has practically become extinct with asymmetrical airplanes. I said that the low power to weight ratio in electrics eliminated hand launching as an option -Wrong!
Howard's A record holder, sporting a 4-turn Astro-Flite FAI 05, weighs about 30 -Oz and has about 100 -sq in wing area (see Photo). Acceleration on the dolly took too long and used up too much battery power, so Joey Mathison was enlisted to launch. It worked twice out of two tries, saving maybe 5 or 6 seconds of vital battery power that would have been used to come up to speed in the dolly.
My B ship accelerates somewhat faster on the ground, and I'm in the pylon before liftoff, so a handlaunch of my 60-oz airplane is not as necessary- besides I'd probably have to find King Kong to do the throwing! More Later, Bill
I've recently discovered that I prefer to fly CLOCKWISE. I'm told that this is an advantage in the PROTO events and F-40. Supposedly, engine torque on take-off prevents airplanes from wrapping the lines. [I personally think that the SPIRAL WASH is a greater factor than torque]
"THE NATS FILE Make sure you can fly the plane or have someone who will. I drove 600 miles and could not find a pilot!!!
Pete Soule e-mailed the following on the subject of propellers;
John,I have measured data on prop inertia and the correct method to compute gyro torques on one of my 2 sites... check it out
After getting there;
- select Aerodynamics
- Then select Aero Notes
There are about 6 articles there -- some of interest to speed and the one on gyro forces.
The so-called 'P factor' (the word is slang for modelers and some pilots) is interesting to think about and for some airplanes is important. It is of no interest at all to speed. In aeronautical engineering the forces and moments introduced by operating a propeller at an angle of attack and under pitching and yawing is called by several names -- most important of which is the "Forward Fin" effect.
For speed the counter clockwise rotation in flight provides a nose up moment that makes a noticeable reduction in the amount of up elevator needed to trim.
With a properly biased horizontal stabilizer , flying the opposite direction won't do much harm. If it improves reliability of takeoff then it is probably worth it. Pete
It's great to hear from you, Pete. The subject of props is confusing to me as I'm sure it is to others.
Pete has got an excellent site, do yourself a favor and check it out!
I do not feel as strongly about treating newcomers differently as I once did. See the NATS FILES
If you are a member of the C/L message board, you know that there is an on and off again discussion on how to attract and motivate newcomers to speed. Scott Newkirk made the following suggestion in this regard.
I think that regulating this for beginners is far easier than we are trying to make it. I suggest the following:
- Get rid of Junior, Senior and open events and replace them with.. 1a) beginner 1b) intermediate 1c) expert
- If you win an event in an AMA sanctioned contest 3 times you are automatically bounced to the next category.
- If you fly an event officially at 80% of the national record twice you are an intermediate. If you fly officially at 90% you are an expert
This is similar to the way the RC aerobatics guys have done their system for years with considerable success.
If you want to have a beginners only event you only allow beginner flyers to enter the event (just like 40's being the maximum engine size for juniors)
If you want to have an engine claim rule put a dollar price on the engine for the event. Anybody can fly any engine they want at whatever they are willing to spend but they had better be willing to lose it for the claim price. You wouldn't see many Zalp's sold for $150 in beginners F2A.
I think it is an excellent approach to a very important issue.
This is described as needed to get the plane to fly TANGENT to the circle. Hold an airplane with the nose pointed at you, notice the frontal area. Now yaw the plane slightly, notice how the frontal area increases. Not only is the area larger, the thrust line is out of trim. In some applications, this serves to keep the lines tight[or slack]. In speed it slows you down. Flying tangent is desirable since it produces the least amount of FRONTAL AREA and HENCE the LEAST AMOUNT OF DRAGand I would guess that if the airplane is TRIMMED SO THAT THE THRUST LINE is not yawed, your powerplant is more efficient.
Think of the FUSELAGE like an oar steering a canoe. YAW [from line drag on the wing tip] causes the "oar" to stick out into the airstream, which SLOWS US DOWN. Because all of it's "WINGS" ARE ON THE SAME PLANE[cowl,wing,stab] An FAI style ship[sidewinder] exposes less of its fuse, cowl etc. to the airstream when out of trim. See the ELIMINATOR II article in the SPEED TIMES ARCHIVES.
USE THE C/L SPEED MESSAGE BOARD to read an excellent discussion on the subject.
Credit must be given to Bill Netzeband for his article on this subject published in the 60's and currently availible thru BRODAKS/PAMPA
Bill added some tips on how to apply the program.
It's the GREATEST. If you are trying to get into SPEED, TRY SPORT JET!. NO PROPS, TORQUE, ENGINE MODS. Look into an upright design. EASY to build, no dollies. Contact JET BILL
JET TANKS. In the PHIRE-PHART construction article, DOC DAVIS describes the 1x1x10 rectangle tank and its construction. Be sure to mount the tank so that it's length is divided BY THE C/G, taking into account that old style uprights had their tanks located in the nose. This would effect trim as the fuel was burned[see the HOT CANARY, scroll down]as you look at the SIDEWINDER[scroll down]you may observe the tank is located so that it's mid-point lengthwise, is closer to the C/G. Les Pardue makes the observation[get Mike Hazel's JET PACK article reprints] that old style[tank in nose] uprights would fly YAWED out because of the weight of the fuel. The concern for this is manifest[big word] in the SUPER BURP, where you will find that the tank has been located so that it runs the length of the fuselage. The engine is located so that it's centerline is on the outboard surface of the fuel tank. The tank is ROUND, so that fuel puddles to the pickup, which is on the outboard wall. The Burp tank is a SUCTION UNIFLOW design so that as the tank pressurises inflight, the uniflow feature meters fuel for a more CONSISTENT RUN. Also, most people have advised that 2 [two] fuel baffles be included inside the tank to PREVENT FUEL SLOSH, which will upset flying trim. The baffles I believe should be 80% of the tank width and evenly spaced.
This is all very interesting, but I think that the CANARY, KEYNOTE and the SHOCKWAVE are WAY COOL!
I assembled a JET TANK. It is 12" long x 1 1/4" high. At 2/3's back it is 1" wide. The front and rear ends are 3/4" wide. It has three 5/8" wide baffles, evenly spaced at 3" apart. The pick up is at the widest [1/3] section of the tank, but not quite touching the outboard wall. I have included both UNIFLOW and STANDARD vents[thanks, MIKE COUTS!]. This tank will be for a SIDEWINDER. It will be REMOVEABLE so that it can be easily maintained or changed[thanks, GORDON THOMAS!] It has two 1/4" O.D. tubes through it widthwise to serve as adjustable tank mounts to allow it to be SHIMMED INBOARD/OUTBOARD. I made the tank out of .010 brass shim stock. IT WEIGHS 4 0Z's!!
Don Carron offers this method of tank building for jets:
...I make my jet tanks from .002" or .003" thick stainless steel shim stock. You can buy it by the rolls at an industrial (steel or metals) supply store. The rolls are maybe 6' long, so you get a lot of tanks from it. About $30 last time I bought some.You can solder it with Sta-Brite and a good pencil iron or tiny torch. A standard propane torch will char it and the solder is then hard to stick.
If you make wedge or coffin tanks with front pickup, be sure to put a high-resistance box baffle up front for the pickup tube. Otherwise, enough fuel is used in starting/launching that surge will uncover the pickup and she'll die every time about 15 feet from the launch. Dispiriting to say the least after a 6 hour trip to a contest :-(
Box Baffle? uh oh...
After speaking withBill Garner I decided to build a sorta SUPER BURP as a SPORT-JET. Comments made in the AQUARIUS"B"PROTO article have got me thinking about the benefits of a HIGH thrust line. The Aquarius has an inverted engine AND the wing is BELOW the thrust line. BILL explains that these features allow the airplane to groove better in windy conditions since the high thrust line tends to induce negative pitch. When coupled with the inverted cowl it must serve very well to combat PITCH oscillations.
Another feature I like about the AQUARIUS is THE BUTTERFLY TAIL. Bill states that if you build it with an inboard elevator, UP ELEVATOR IS ALSO OUT RUDDER. THIS IS SAID TO IMPROVE TAKE OFF HANDLING. If this is correct, why build any WHEELED SPEED SHIPS WITHOUT A BUTTER FLY? [the rules in .21 proto prohibit butterfly tails unless the model is SCALE]
The BURP type airplane certainly has a high thrust line and a LOW DRAG CENTER.
Additionally, the BURP tank is located along side the fuselage and is INBOARD of the thrust line, so that the tank feeds outboard, The tank is uniflow and CYLINDRICAL. If I'm correct, the tank will be 15.5" long, 1.25" front end diameter and .75" back end diameter.WITH A BUTTERFLY TAIL, OF COURSE. Anyone have an old pool cue?
CENTER OF DRAG. In an article about trim and balance, LES PARDUE talks about THRUST-LINE in relationship to the "CENTER OF DRAG". Consider an UPRIGHT vs a SIDEWINDER JET. The upright has its thrust line above the DRAG CENTER and should tend to fly DOWN-PITCHED. A sidewinder has its THRUST-LINE BELOW THE DRAG-CENTER and should tend to fly PITCHED UP. The implications for trim are obvious and probably explain why MR. HOYT balanced on the LEADING EDGE. A SIDEWINDER also must tend to YAW INBOARD SINCE THE LINE AND FUSELAGE ARE INBOARD OF THE THRUST LINE, hence the nessessity of an adequate RUDDER. The article quotes CHARLIE DAVIS as saying that if a SIDEWINDER inflight does not have it's outboard wing in-line with the control-line, then it's not "...going anywhere [fast]...". I take this to mean that some YAW is GOOD!!!
Now that I've seen the ROSSI jet, I know that the design parameters of jets could use further development.
I know that DOC DAVIS did some work with asymmetric designs and that Jerry Thomas' IRONSIDES designs work well, but I can't help feeling that there is a better way to configure.
I do think that the best way to get fuel to a jet is the HOYT/DAVIS SIDEWINDER configuration but the best way to get a good stable airframe is the THOMAS/PARDUE/LANGLOIS SUPER BURP/IRONSIDES style with the high thrustline.
These parameters make sense to me.
I spoke with "PARTNER" re: "THE ELIMINATOR" upright asymmetrical. I asked him why Ned said this style doesn't work. He told me that not only is it more susceptible to drag from YAW, the cowl drag tends to induce A PITCHED attack angle. This drag on the cowl pitches the airplane POSITIVE [and slows you down]
Ned told me that if he could[the tank is in the way], he would insert his WINGS at the PAN/FUSELAGE junction on his UPRIGHT. His placement of the wing above the CRUTCH is a compromise that is part of the UPRIGHT design characteristics. This placement above the "THRUST LINE" futher induces pitch as a result of drag on the wings. To balance this, one must trim the stab[more drag] or fly nose heavy[reduces the effectiveness of the wing and upsets landing and overall handling characteristics].
"...Brownies "D"..."
I went to Brownies Hobbies on Staten Island and saw George Sr.. He is a great guy and treated me to a tour of his shop. One of the MANY [as in lots and lots] of speed ships he had there was his old piped OPS .60. It was one of the first to go 200mph and is a wicked looking rig.The reason I want to mention it is the COWL SHAPE. It [the cowl] has it's leading edge tapered WAY BACK, as if to look like a wart rather than a typical upright cowl. I think this shape must give LESS RESISTANCE [drag] both from prop wash and airflow. It looks very much like cowls seen on Russian F2A's.
"PARTNER" went on to say that the "LAYDOWN" cowling on a true "SIDEWINDER" becomes another lifting surface, making the entire airplane a "FLYING WING". The fact that all of the "wings" are on the "THRUST LINE" minimizes any drag that would induce pitch.
As an illustration of this, consider the "HOYT SIDEWINDER" jet design. In order to clear the pipe, the wing is 3/4" above the "THRUST LINE". To compensate for this, the design calls for SOME degree of positive stab incidence[a drag producer] I am making my stab adjustable, with stab area 50% of the wing area. Hopefully the increased stab area will produce additional lift and less drag than a smaller stab set positive.
The famous "PINK LADY" designs are 50% stabs[I've been told that they are balanced as far back as 50% of the average chord]
In any event, we need to hear from NED on how he trims his upright. It can't be all engine!
Made a visit to BOB WILKIE'S, he had an old article on the TOP C.A.T. "D"[C] speed ship from the early 60's. The author, Clifford A. Telford, talks about his design having an overly large RUDDER. He says that in a CROSSWIND, this rudder offsets the effect that the wind has on the large COWL. I thought this was interesting as he said that a rudderless upright is subject to YAW OSCILLATIONS from wind hitting the cowl. These oscillations would certainly slow you down.
Furthermore, "C.A.T." says that a LIFTING STABILIZER KEEPS THE AIRPLANE FROM CLIMBING WHEN HEADED INTO THE WIND, and has no effect with a tail wind.
It follows then that a FAI "SIDEWINDER" SHOULD NOT HAVE too much of A RUDDER SINCE THERE IS NO COWL TO OFFSET THE WIND EFFECTS. It seems that you must consider SURFACE area NOT ONLY IN THE PITCH PLANE, BUT ALSO IN THE YAW PLANE. This would apparently refute Francis Reynolds claim that C/L models do not need a rudder.
It seems as though you must consider whats fore and aft of the YAW plane[as far as surface area] as carefully as you consider wing vs. stab area.
NOW, consider the point that MIKE FISKE makes in his SPEED TIMES "SPORT-JET" article recently. He says that YAW caused by the wind's effect on the rudder as the ship travels up and downwind automatically TRIMS FOR PITCH BECAUSE ON A TWO LINE SHIP THE AIRPLANE YAWS BUT THE BELLCRANK DOESN'T!!!![assuming the pilot can hold the handle steadily] This alternating pull on the lines moves the ELEVATOR. IF the UP line is in front of the down line, then when the WIND is at your BACK, the plane YAWS in, pulling on the DOWN LINE so that as your ship turns into the wind the down trim fights the LIFT imposed by going into the wind.This WEATHERVANE EFFECT IS BENEFICIAL[according to Mike]since the airplane will automatically correct for pitch attitude changes caused by the effects of the wind.
I looked at some FAI plans and noticed that the planforms show a rectangular surface area, actually a AFT of C/G AREA that corresponds with the area ahead of the C/G. IS this a feature or is it there"...'cause it looks cool..."?
HUH?
THERE IS A LOT MORE TO FLYING IN A CIRCLE [FAST] THAN JUST THE ENGINE!!!!!
Paul Haley showed me a clown racer with a very large inboard offset. He said this was done to improve ground handling. I set my F40 strut on the inboard edge of my pan. The airplane is THE MOVE, by MIKE HAZEL[plans availible from SPEED TIMES] My landing gear is 5/32 music wire, so there is NO DRAG FROM HAVING A SOLID GEAR AT TOO CLOSE OF AN ANGLE TO THE PAN. This is a "MOVE" design feature.
Doug Gray and I went to fly at WESTOVER recently and got into a conversation on F40 landing gear. I think that the popular aluminum streamlined gear is a wing [and creates drag from prop wash] I think that a wire gear with a streamlined tubing cover would be cleaner. Of course everyone is using the flat gear [except me] so what do I know?
I've been flying my F40, THE MOVE by Mike Hazel powered by a MVVS GRRT two piece. A good start for speed.
Take-off is the name of the game in F-40. A lot of it is the pilot, but some of it is the set-up.
An old RAT RACER gave me the skinny on setup;
I think F-40 is a great place to start as a speed flyer. Two lines, mini-pipe, lots of good engines. You just gotta get the takeoff down and your gonna have FUN! Try to use a hard tank. If you need a plan for a 40 tank, e-mail me and I'll e-mail one to you.
I put out an A.P.B. to request information re:AQUARIUS B PROTO. BILLY HUGHES wrote to suggest that I try to reach ELMER HUFF, who teamed with BILL GARNER and JOHN BARTLEY to campaign the AQUARIUS in the 70's. This team set many records in all classes of speed. I spoke with ELMER at length and then contacted BILL GARNER. Both men were very happy to speak on the subject of the AQUARIUS. Bill was very helpful at explaining the design features such as the HIGH THRUST LINE etc. [as previously mentioned] and he recently provided me with a plan.
Meanwhile, I had asked BILLY HUGHES to comment on some of the design features of the AQUARIUS. Here are MY QUESTIONS and his comments:
I've been told that inverted engines are faster but difficult to start...
"...it is really not any more trouble [to start]. Just don't flood the motor when you fill the tank.[see ed note below] My last RAT RACER [1984 OPEN NATS WINNER] was an inverted design. No problems. Do I think they are faster? Yes I do. Why??? The drag of the landing gear is less.[the gear is shorter, ed.]
I also asked Billy about the cowl being BELOW THE THRUST LINE.
"Do I think the cowl [inverted] improves handling? NO! They tend to be VERY hard to get into the air. [prop wash on the cowl at take off speed? ed.] The pilot has to be "on his horse" when the model is launched. Unless the motor turns clockwise or the model flys clockwise the torque of the motor turns the model at the pilot. On my RAT and others, the acceleration is not very high. LOTS OF FUEL. 4oz back then. And a heavy model. On an F-40 [or .21 proto] they can come in on the pilot easy. They take off like a rocket, if they are good ones! THIS problem I feel may be solved with the SUB-RUDDER that BILL NUSZ began using on his F-40. But I'm not sure. The other drawback with an INVERTED ENGINE is that if you HIT the ground... it can cost alot of $$$$, the motor takes it on the chin!Bill
Thanks, Bill, that was insightful! It gives all of us contemplating design some SOLID comment based on experience.
[ed. note-I hold the airplane nose up and keep it nose up until I hit it with the starter]
BILL WISNIEWSKI'S PINK LADY,any size, BUT ESPECIALLY A "B" [It looks like something LOCKHEED would have built]THE HOYT SIDEWINDER [anything more compelling than one of these?]
HAROLD STEVENSONS NEW ANGLE III [weird, ain't I?]
THE CLEM/BEASLEY/KIRN SHOCK WAVE [another LOCKHEED product]
THE KURTH PEANUT [I built one last summer T/D, suction uniflow, 35' lines. How can anything so small...?]
CARL CHINAS VIPER II [if DARTH VADER built a speed ship, the VIPER would be it!!!]
ANY PULSE JET ENGINE, BUT ESPECIALLY THE AWESOME WARRIOR!!! [I fell asleep holding my copy every night for a week]
SUPER TIGRE 29X [I have one]
ANY TEXAS QUICKY RAT [hot-rods, shade tree's, beer]
THE McCOY .60 GLO [I might buy one, DOOLING= INDIAN, McCOY= HARLEY-DAVIDSON]
MIKE HAZEL's F-40, THE MOVE [it's so basic, like a chopper]
BILL GARNER's AQUARIUS "B" PROTO. WHY DID YOU GUYS STOP THIS EVENT?!!!
.This is my hobby, so I try to have fun! The old stuff is COOL!!!
Need some tank dimensions? I received a plan for F-40 and .21SPORT tanks that were supposedly used/designed[?] by BILL NUSZ. These are tall and NARROW, making it very easy to keep them inboard of the N/V. Go to "...the picture page..."
Bladders: I have not had much experience with bladders. COFFIN[1/3-2/3 wedge] SHAPED HARD TANKS: To ME, this is the only shape tank that makes sense for speed. AT SPEED, FUEL IN YOUR TANK GOES TO THE OUTBOARD WALL AND FORWARD!!! A coffin tank is actually just half a coffin[the coffin corner goes outboard] As stated elsewhere, I think the OUTBOARD EDGE of the coffin should be in line with the CENTERLINE OF THE ENGINE.[centerline of the VENTURI on rear intakes].If you mount your tank TOO FAR OUTBOARD, some of the fuel might have to flow against centrifical force. This will effect your N/V setting. Think of trying to empty a bucket by punching a hole in it HALFWAY DOWN THE SIDE RATHER THAN AT THE BOTTOM of the bucket. HALF of the buckets contents will empty easily by force of gravity, the other half will have to be pumped out. If you have a hole at the bottom of the bucket, all of the contents will flow out from gravity alone. [I hope this is a clear analogy] The coffin shape allows fuel to pool at the coffin corner. You should have your pickup and vent line in that area[UNIFLOW VENTING OF COURSE]. This type of tank keeps feeding even if you are out of trim [YAW]. In his WILDFIRE construction article, PARTNER advises to make your tank mounting adjustable. That is for INBOARD/OUTBOARD ADJUSTMENT. This will allow you to set your needle valve on the ground for a take off and set your in/out adjustment for FLYING. SHIMMING YOUR TANK INBOARD WILL ENRICHEN THE MIXTURE, OUTBOARD WILL LEAN IT OUT. NICE, HUH?
I'm starting to think [ALWAYS dangerous] that you do not need the front part of the WEDGE. If you make the out board wall of your tank so that the FRONT is further out than the rear[like the FRONT FEED article describes, scroll up] shouldn't the tank work just as well? I'll have to see when I fly my FRONT FEED .21.
Fuel has weight[mass?] at XXmph, centrifical force has the effect of increasing the line pull of an airplane and has the same effect on the fuel. This weight/mass increase effects the pressure/rate that the fuel is supplied to the engine. As the fuel is used, the FUEL HEAD, or width of the fuel diminishes. As the FUEL HEAD diminishes, PRESSURE caused by CENTRIFICAL FORCE also diminishes. This effects the pressure/rate of the fuel supplied. At the start of a run with a STANDARD VENT TANK, the engine is supplied more fuel[richer]. At the end of the run, the engine is getting less fuel[leaner]. The end result is that your run is INCONSISTENT. Since you cannot adjust your needle valve in flight, you must find a way to fight the effects of CENTRIFICAL FORCE. A UNIFLOW TANK creates a PARTIAL VACUUM ON THE INBOARD SIDE OF THE TANK TO FIGHT THE EFFECTS OF CENTRIFICAL FORCE. This VACUUM keeps the fuel flowing at the rate that air is being BLED INTO THE TANK. THE TRICK is to keep the the tank end of the vent immersed in fuel[WET] THROUGHOUT THE ENTIRE RUN. THIS MEANS THE VENT MUST START AT THE INBOARD SIDE AND END AT THE OUTBOARD SIDE OF THE TANK. Since your fuel is now metered, your run will be more consistent from start to finish. To me uniflow venting is best described by thinking of a soda bottle being emptied. If you tip the bottle slightly, soda will spill out in a smooth flow, again through the force of gravity. HOWEVER, if you turn the bottle upside down, a [partial] vacuum is formed at the closed end. In order for soda to escape the bottle, air must enter the open end and travel up through the soda to fill the vacuum. Soda flow is metered by the amount of air GURGLING through the soda as well as the effect of gravity. If you were to punch a hole in the closed end of your bottle, air would be able to enter, filling the vacuum and releasing the soda. If the hole were large enough thre would be little or no GURGLING, the soda would flow freely. A STANDARD VENT TANK IS LIKE THE BOTTLE WITH A HOLE AT BOTH ENDS, it has its VENT INBOARD and fuel flows freely, the rate of flow and pressure increasing as speed increases CENTRIFICAL force.This increased flow could overcome your NEEDLE VALVE SETTING resulting in a OVER-RICH condition. THE UNIFLOW TANK HAS ONE END OF IT'S VENT INBOARD,OPEN TO THE ATMOSPHERE. The other end enters the tank and ends near the OUTBOARD WALL of the tank. This end stays submerged in fuel while on the ground and throughout the flight, creating the previously described PARTIAL VACUUM AT THE INBOARD SIDE OF THE TANK. PARTIAL VACUUM fights the effects of CENTRIFICAL FORCE, METERING the flow of fuel and keeping your N/V setting constant[or more consistent]. A CLOSE TO CORRECT N/V setting on the ground will stay close in the air. Making the tank ajustable in or out will allow you to fine tune even further[WOW]. It appears that most guys design their tanks so that the UNIFLOW VENT goes dry[is exposed to air] right at the end of the run. If right this serves to enrichen the mixture just before the engine quits.[this is good] Some applications such as SIDEWINDER JETS may be better with STANDARD VENTING. In HOYT'S SIDEWINDER CONSTRUCTION ARTICLE[1971], he mentions that the sidewinder design allows you to take off in a lean condition. He states that a JET TAKEOFF with a RICH CONDITION is difficult because a rich running jet will CUT OUT at the SLIGHTEST BUMP. He uses the fact that standard venting will increase fuel-flow at speed, giving the engine ALL the fuel it can handle as it reaches speed. This design takes advantage of CENTRIFICAL FORCE TO PRESSURIZE AS WELL AS ENRICHEN THE FUEL FEED AS SPEED INCREASES. ***THANKS TO PAUL HALEY FOR HIS EXPLANATION*** WHAT SAY YE??[Did anyone say "PASS THE SURGICAL TUBING"]
I believe that your fuel tank outboard wall should be inboard of the NEEDLE VALVE ORIFICE of your engine. I think that this is one reason why assymetrical airplanes are a good idea. It appears to be much easier to insure tank location inboard of the engine center line than on an upright.
I saw an article in the AMA magazine about FRONT FEED TANKS. The article was in the C/L RACING column. I am going to try this setup on a K&B .21 powered GOODYEAR size monoline trainer. The details are simply a round racing tank[a pan tank?] that you take the front cover off of, cut the can at an angle[more aerodynamic], replace the cover, use an icepick to punch two holes on the outboard edge of the front cover[hence the name "front feed"] and solder a feed and a uniflow line in. The feed line is 1/2" into the tank at the centerline. The pressure line is slightly inboard aligned, above the centerline. Be sure to mount the tank so that the front of the tank is outboard of the rear. I'll let you know how it works for me. I crashed shortly after takeoff, giving down in an up situation. The engine was surging, I may have placed the pickup too close to the vent.
Alas, my YAK is no more. The last two times I flew I had a stooge incident. Last time, old stoogie let my new/old monoline trainer go a little early. Minor damage, I dusted her off and went onward with no more problems. Yesterday, old stoogie wouldn't let THEYAK go at all. I yanked on the line and all of a sudden had a YAK ATTACK. She was bearing down at me, then shot past and snapped the lines[.018 stranded]becoming a free flight with a heavy wing loading. Needless to say, I did not max. The YAK is now a outboard assymetric.
Not to worry, I am gonna transfer to a RINGMASTER that has been hanging around. The OS is going right in.
I gotta be more careful with old stoogie.
I'm running out of airplanes. Four flying sessions this spring, three crashes. But two were very spectacular!
Ned's epoxy fillets worked. I now have the most nose heavy RINGMASTER in the northeast. It pulls like a horse. Good trainer for speed and it cost about $120 to build.
TRAINING ON SHORT LINES. CL in general and cl-speed in particular is not a solitary pursuit. You need friends![...anyone want to launch my FAST-JET...?"]
To that Question Don Carron writes...
...Bring that sucker to Knoxville and Bryce and I are your men. Bryce is the youngest person ever to fly a jet according to memory of Dimmit, Doc, Gene, and Partner. He flew at 9 and competed in Sport Jet at 10, beating doc once....wheeee!!! not a happy Doc that day. Bryce unoficially bettered the Jr. record in .21SS at the 96 Nats, but ran out of fuel before the end of the 7th. That old Garzon ship was flat spinning. After ten years flying and launching with dimmit, Mike, Doc, and the Texas bunch, we have moved to TN. Haven't heard a jet run in over a year. :-( Cheers/Don Carron Rockford TNDon and Bryce, we gotta get a circle in every town!
However, the biggest obstacle for me has been flying sites that would allow me to practice with actual speed equiptment. That's why I like short lines on slightly overpowered sport planes.
I have plans for two different combat airplanes that use SPEED PANS!. This will allow me to fly off of grass using speed engines. The airplanes are the COUNT CLIPPER, plan availible from BARRY BAXTER and the KITE, plan availible from GLEASON ENTERPRISES. Flying sport planes,I can get handle time almost anytime at lots of sites. Most of the pro's suggest short lines to train, especially mono-liners. My first attempt with mono-line was a disaster. Then Uncle Ned suggested I try a 1/2a profile with a black widow on 30' lines. INSTANT SUCCESS! I later went to 25' lines, then gave the plane away to a friend. The trainer I currently use is a QUICKEE-RAT type profile with a FOX 36x MKIII. This is flown on 40' .024 monoline. This "flight simulator" gives me good handle time.
WING AND STAB INCIDENCE. when talking with NED a while back, I asked him about positive incidence at the wing root on assymetricals. He said this was not needed and you should build 0/0. Later on , Partner said the same thing. Several speed flyers have told me to make stab incidence adjustable to trim for pitch attitude rather than trim by adding or removing weight. I think your controls/wing in relation to thrust line effect FLYING TRIM [see #18, this document]. When building my F-40, I built and balanced the fuselage, then built the wing planform. I did this to insure that the wing crutch would be placed on the tie downs, but more importantly that C/G of the fuselage coincided with 25% of the wing chord. I also was able to have the leadouts exit on the c/g, but I did not consider line drag so I probably have too much inboard yaw at speed.
I would have liked to have made adjustable leadout guides, but...Well, maybe next time.
MVVS ENGINES. This is not a plug, but one reason that this page exists is to help novice speed flyers. My first competition speed plane is a F-40 powered by an MVVS GRRT .40 I entered it, it flew and logged two officials. These were it's first two FLIGHTS. This engine is available, I got one for about $120. It did 129 mph with no development and on command[during a contest]. Like I said, THIS ISN'T A PLUG... BUT IF YOU WANT TO GO FAST IT MAY BE THAT AN MVVS IS A GOOD PLACE TO START. I spoke with Pat Rose, a speed flyer from England, who has used this motor to go 190 in English F-40[monoline, 40% nitro, tuned pipe].
"...one minute, I said ONE MINUTE!!!..."
Mike Couts told me to get my airplane to work everytime I fly, THEN WORRY ABOUT GOING FAST LATER! On my next attempt to fly it [a practice session back home] IT DID NOT WORK!!! PARTNER offers this advice to us beginners,"...pick one or two events and get good at them..." This will allow you to become consistent. You should base your efforts on sound engineering. Build consistency into your model. Stay away from experiments in your contest ships. If you drive 1000 miles to enter a contest you at least want an official flight logged. There is no prize for most original. Do not try to be Ned Morris unless you are Ned Morris.
While we are on the subject of MAD SCIENTISTS, have you ever thought about trying...
...a pusher canard for speed. Maybe 1/2A PROTO? No prop turbulance over flying surfaces. Engine cooling/exhaust problems? PROPS?...a DELTA wing sport-jet? Look through the jet pages in MY FAVORITES,the pulse jets are mostly DELTAS.
...LAMINAR FLOW AIRFOILS? What is the advantage,if any, in our "low speed" applications?
...putting a bellcrank halfway out on your wing in SPORT-JET and 1/2A PROTO? Since the controls are already exposed, you save on some drag cause your lines are a little SHORTER. I did this on a PROFILE TRAINER powered by an MVVS .15. The thing flys fine, just like MIKE FISKE said it would in his SPORT-JET article in SPEED TIMES. There is no LEADOUT GUIDE, just a button bellcrank. I think you do need a rudder.
Too many[crazy?] ideas, too little time. When I look through old modeling articles and magazines, it seems that people back then would try to do more experimenting. I think it's fun!
The following is an excerpt from an E-MAIL we received from BILL STEWART about DELTA WINGED JET-SPEED.
"...You mentioned DELTA SPEED. At the 1953 Nationals a guy from Washington, DC showed up with a clean, well constructed Dyna-jet delta...it was a 60 degree delta, about 18"[wing] span, U-control, balanced on the front line...the airplane was stable but slow. On the last flight with a storm moving in and the wind picking up,...the cross-wind sectors of each lap the plane was almost uncontrollable, with the wing rocking and the nose corkscrewing.After a couple of years in aero engineering I understood that due to the DIHEDRAL EFFECT, A FLAT DELTA produced a coupling with the crosswind that resulted in a sharp, rapid DUTCH ROLL, as the relative wind angle changed, relative to the wing leading edge. The moral of the story is IF YOU BUILD A DELTA, USE PLENTY OF NEGATIVE DIHEDRAL. FOR A 60 DEGREE DELTA, NO LESS THAN AN INCLUDED ANGLE OF 15 DEGREES[71/2 degrees per side]..."
The following are excerpts from a response to a letter I sent to SUPER-SABRE [Ned Morris]!
"...I hope you can read my writing. Got your nice letter[a print-out of the SPEED REVIEW]. Full of questions and answers. Good questions and few of the answers were good""...This hobby is full of UNPROVEN[wrong] CLICHES or opinions. Examples; degummed castor oil. Absolutly wrong, widely disseminated...other untrue things: put 2-3 degrees of inthrust on a speed model to reduce line pull. This will reduce line pull by SLOWING THE MODEL DOWN slightly. Not good...polish the bearing bores in your crankcase to let the bearings slip around for a free alignment...this has RUINED many crankcases, the crankcase must hold both bearings tight!"
"...there are several reasons[that] the assemetrical models are better, TANK LOCATION NOT NECESSARILY ONE OF THEM[ouch]. But, the tank has to be right. Inboard of the NEEDLE-VALVE is important!Another [advantage] is lowering the line-drag by covering the HIGHEST DRAG PART OF THE LINE[with the long inboard wing] Also, reduced wing and fuselage interference of the wing and stab by 1/2 or more."[S/S gives a frontal view of an assemetrical ship, pointing to the top of the wing/fuse junction as a place of interference drag and the bottom of the junction as a place that must have a LARGE ANGLE between fuse and wing]
"LINE RAKE...there was an article by BILL NETZEBAND about line rake. What it amounted to was the C/G at 20-30% of the MEAN AERODYNAMIC CENTER WITH THE LEAD-OUT CENTER ABOUT 5% BEHIND THAT."
"...PRESSURE FEED is not a cure for a BAD TANK SET-UP, to get even fuel feed you must run with a tighter needle valve set[more suction or closed more]. TO do that, pressurize the tank or put a smaller venturi restrictor in the engine. Also, move the tank inboard to get more fuel in the air."
"...two guys from OHIO...had a SIDEWINDER JET with a cylindrical tank. WORKED GOOD!"
"...monoline models balanced at the leading edge...WHY? [Bill]Wisniewski's airplanes have 50% stab area[of the wing] and balance at 50% of the MAC...[they are] fast and stable. I[he] use a 25-30% C/G with a 33% stab..."
"...build contest winners, not record breakers...the records will come when you least expect it..."
WE love to hear from guys like SUPER-SABRE!!! ALL of you fellow ROOKIES TAKE NOTES!!!
LIL TIGER. AMA magazine has Dave Hull's 1/2A PROTO as a feature. I've talked to lots of people who are buying CS .049's and building 1/2A's. GO FOR IT! My first attempt at a true speed plane was DALE KIRNS TORKY. WHAT A GREAT TIME!!! It met it's demise using 42 foot lines in a 40 foot parking lot. Hit a sign on the 1st lap.
"...yeah it's ok if you use my name, most people know that I am outspoken...""Don't take what some of the so called experts [say] as the WHOLE TRUTH! Look at what is running the fastest. F2A models are OUTBOARD SIDEWINDERS because they are faster [than other designs]"
"They [F2A] use FRONT INTAKE motors because they have less internal drag, i.e. not turning a rotor. They use SUCTION/UNIFLOW TANKS because they work, bladders break. Crankcase pressure GOES DOWN as RPM goes UP, not good. You need a switch to use a PRESSURE SYSTEM ON A PIPE [regulator? ed.]. Just something else to break. Using [exhaust] pipe pressure is not a good idea either. The pressure increases FASTER THAN NEEDED, the motor usually floods out [just] as the motor hits the pipe."
"And REMEMBER, some people BUY their speed, the guy I want to follow makes it himself, he REALLY knows how to make things THAT WORK. So, not everyone is an EXPERT. Watch the guys who are setting the records or winning the NATS, know if they purchased the equiptment or MADE IT THEMSELVES, BEFORE YOU BELIEVE WHAT THEY TELL YOU..."
Thanks, Bill. Great stuff! Like I said at the top of the page, you gotta find out what works. Football coaches COPY the schemes of other SUCCESSFUL FOOTBALL COACHES. FIND OUT WHAT WORKS, FIND OUT WHY,
THEN DO IT!!!
I sent Dave Rolley an inquiry re:THE CONTROL-LINE SPEED MESSAGE BOARD. This is his reply;
"...it seems like a GOOD IDEA...I think I entered [most] speed events for this years NATS...my son did the same...we'll have fun no matter how it turns out.I enjoyed the comments by Billy Hughes. I know at least one of the BUY THE TROPHY types...this guy gets upset if he doesn't get first. He can tell me what...but he CAN'T TELL ME WHY!!!Winning isn't the joy, solving problems and improving MY PERFORMANCE IS!
Dave was a top 10 C/L carrier competitor who realized that in his zeal to compete, he LOST HIS HOBBY. He adds that he likes the ATTITUDE of the people he finds at the speed circle and that most [but not all] of the speed guys welcome newcomers.
I must add that EVERYONE THAT I SPOKE TO AT THE NATS WAS VERY HELPFUL AND ENCOURAGING I think that the NATS probably should be for only the best competitors, but the reality of the situation calls for a little tolerance for guys like myself. I do believe you should HAVE YOUR S--T TOGETHER IF YOU PLAN TO ENTER 1/2A, A, B, D, JET AND FAI. But 1/2A PROTO, F-40, 21 SPORT and 21 PROTO WERE DESIGNED FOR PEOPLE TO GET INTRODUCED INTO THE WORLD OF SPEED, all of these events have to be kept as "INTRO" events, if you discourage people from these events, you will cut off your nose to spite your face!
Part of "intro" would seem to be, "CAN YOU GET YOUR AIRPLANE CONTEST READY?"
Look at DRAG RACING. There is TOP FUEL for the PRO'S and BRACKET RACING for the SPORTSMEN. It's all racing, isn't it?
I am mainly a sport flyer with a taste for FAST. Going fast is not a something you may easily achieve on your own. Everyone needs SUPPORT
The object of the game is to INCREASE participation so as to increase political clout both in the Modeling community and the community at large.
The nature of speed seems to be thus;
In addition to what is needed for SPEED, maybe what is needed for control-line in general is to organize SPEED, RACING, CARRIER and COMBAT into a kind of UNION. All these events have similar problems. Why not assemble into one group and take advantage of the resultant numbers?
Has this ever been tried?