| [Statistical Computing: ] |
f(x,y)for x=0,1,...,10 and y in [0,1]. By inspection we conclude that the full conditionals are10Cx yx+3(1-y)14-x,
| X|Y=y ~ Bin(10,y) |
| Y|X=x ~ Beta(x+4,13-x) |
ranbin(-1,n,p). SAS has no direct command to simulate from
Beta distribution. We need to use the following result to do this:
Exercise:
Write a SAS module ranbeta(seed,a,b) to generate from
Beta(a,b) distribution. Use the rangam(seed,a) command
to generate from Gamma(1,a) distribution.
|
 |
genX = J(100,1,0);
genY = J(100,1,0);
do i = 1 to 100;
X = 5; Y = 0.5; /*Arbitrary initial values */
do j = 1 to 200;
X = ranbin(-1,10,Y);
Y = ranbeta(-1,X+14,13-X);
end;
genX[i] = X;
genY[i] = Y;
end;
|
| Exercise: Make the histograms of X and Y separately. |
 and
and 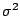 in the following Bayesian set up:
Model: X1,...,X10 iid
N(
in the following Bayesian set up:
Model: X1,...,X10 iid
N( ,
,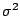 ), where
), where  has a N(0,1) prior
and
has a N(0,1) prior
and 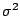 has an independent inverse gamma(1,1) prior. The
posterior full conditionals are
has an independent inverse gamma(1,1) prior. The
posterior full conditionals are
 | |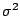 ~ N(10 ~ N(10 /( /(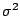 +10), +10),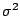 /( /(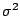 +10)) +10)) |
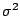 | | ~ inverse gamma(9,T), ~ inverse gamma(9,T), |
T = 1+0.5(Xi-
)2.
| Exercise: Generate 20 points from the posteriors using the one-long-chain approach with burn-in=200 and gap=30. |
Let us write a SAS module to run this chain. First store this matrix in a variable called
0.1 0.4 0.5 0.3 0.3 0.4 0.6 0.4 0
K.
 |
start MC(K,current);
U = ranuni(-1);
if(U < K[current, 1]) then
next = 1;
else if(U < K[current, 1]+K[current, 2]) then
next = 2;
else
next = 3;
return(next);
finish;
|
%include it. Now
generate 100 samples from its limiting distribution using a burn-in period
of 20. Find the proportion of 1's and 2's and 3's in the generated
sample.
Exercise:
Use the eigvec function in SAS to find the limiting
distribution of the MC. The command
|
hij = min{(jkji)/(
ikij),1}.
 |
pi = {0.3, 0.5, 0.2};
do i = 1 to 3;
do j = 1 to 3;
ratio = (pi[j]*K[j,i])/(pi[i]*K[i,j]);
H[i,j] = min(ratio,1);
end;
end;
|
 |
start fMC(K,H,current);
U = ranuni(-1);
if(U < K[current,1]) then
proposed = 1;
else if(U < K[current,1]+K[current,2]) then
proposed = 2;
else
proposed = 3;
U = ranuni(-1);
if(U < H[current,proposed]) then
next = proposed;
else
next = current;
return(next);
finish;
|
Exercise:
Run the filtered chain to generate 100 samples from its stationary
distribution using the same burn-in period as before. Compare the
empirical proportions with  . .
|

 The degree of
a vertex is the number of edges meeting at it. The degree of
a vertex is the number of edges meeting at it. |
At each step we generate a random number i from Discrete Unif{1,...,d} and follow the i-th edge from the current vertex if there is such an edge. Otherwise, we stay where we are.To filter this proposal chain to converge to any given distribution
 on the set of vertices, use the filtering probability
on the set of vertices, use the filtering probability
hij = min{Note that d does not enter into the picture since the proposal chain in symmetric. In particular, if we always accept the proposal we shall simulate from the uniform distribution over the set of all vertices. Now let us use this concept to simulate from the uniform distribution over all the possible 15-puzzle configuration reachable (in any number of steps) from the following start configuration:j/
i,1}.
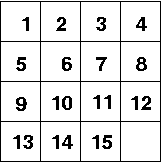 |
| Start configuration |
 |
A = shape(1:15||0, 4, 4}; |
1:15||0 is a (row) vector of length 16: it starts with
1,2,...,15 followed by a 0. The shape function shapes the
vector into a 4 by 4 matrix.
We shall denote the 4 possible moves by 1,2,3
and 4.
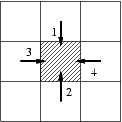 |
| The four moves |
A as an input. The blank position in A is at the
(r, c)-th entry. We are going to make move
i.
 |
start puz15(i, r, c, A);
if(i=1) then
r1 = r-1;
else if(i=2) then
r1 = r+1;
else if(i=3) then
c1 = c-1;
else
c1 = c+1;
if(r1<1) then r1=1;
if(r1>3) then r1=3;
if(c1<1) then c1=1;
if(c1>3) then c1=3;
A[r,c] = A[r1,c1]; /* The (r1,c1)-th tile moves in blank place*/
A[r1,c1] = 0; /* (r1,c1)-th place is now blank */
finish;
|
randuni for this purpose. %include that file and
write
 |
A = shape(1:15||0, 4, 4}; r = 4; c = 4; i = randuni(1,1,4); puz15(i,r,c,A); |
| Exercise: Now run the chain for 500 burn-in steps to generate one random configuration. |